Как игра Zenless Zone Zero обманывает своих игроков
Ради интереса, я решила загрузить статистику своего аккаунта на фанатский сайт, zzz.rng.moe. Где обычные игроки делятся своей статистикой гача круток.
Загрузив её, я увидела цифру 20% побед, в игре, где твоя победа 50 на 50.
Грустно улыбнулась своей "удаче". Сайт оценил удачу моего аккаунта, как хуже 90% пользователей.
Печально конечно, но на отдельно взятом аккаунте это цифра ничего не значит. Из любопытства, я решила посмотреть различную глобальную статистику.
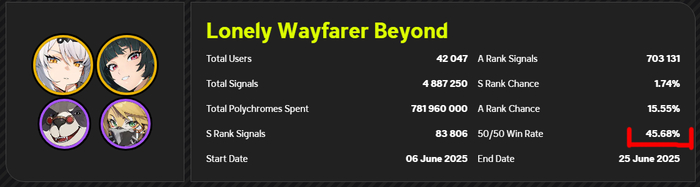
Просматривая различные цифры и графики, я открыла статистику последнего баннера с персонажем Исюань. И мне попалась на глаза цифра в 45%.
Это цифра побед в среднем у всех игроков.
Я удивилась.
Все кто знаком с законом больших чисел, должны были заподозрить, что-то неладное.
Поясню.
Закон больших чисел в теории вероятностей описывает, как среднее значение случайной величины, полученное из большого числа независимых испытаний, сходится к математическому ожиданию этой величины.
А теперь напомню, у нас игра в монетку, орел или решка, математическое ожидание 50%.
Вы не можете подкинуть монетку 20000 раз и получить 45% орлов. Как говорится вероятность этого "КРАЙНЕ МАЛА". Настолько мала, что это 51 ноль после запятой.
Я подумала, "Ну ладно, может игрокам сказочно не повезло (Нет). Или может какой-то неизвестный мне фактор, повлиял на результат."
Решила проверить другой баннер. И открыла баннер Вивиан и увидела все те же 45%.
Опять то же самое. Ладно, решила начать с самого старта игры. Открыла баннер персонажа Эллен Джо.
Увидела цифру в 52%. Прикольно, подкрутка 2% в пользу игрока.
Все последующие баннеры, все как один показывали цифру в среднем 52%.
Так продолжалось вплоть до Астры Яо, 47%.
Понятно, тут они решили чуть-чуть залезть в карман игроков, решила я.
Но следующие баннеры, становились всё хуже и хуже для игроков.
Эвелин, 42%.
Солдат 0 Энби, 38%.
Дойдя до Хуго Влада я начала откровенно РЖАТЬ, МЕНЬШЕ 32% процентов! А его сигнатурное оружие, 46%! При том, что вероятность победы при крутке оружия 75%.
Я оценила тонкий юмор разработчиков. Персонаж вор, ворующий у богатых шедевры искусства, чтобы жертвовать деньги бедным, просто наглейшим образом, ворует у бедных игроков деньги, чтобы отдать их до смешного богатой компании miHoYo.
Увидев 46% в баннере с оружием, я решила посмотреть их и у остальных персонажей. Обнаружила, что всё было максимально честно, 75%.
Но начиная с Мияби цифра начала "плыть", 65%.
Я так понимаю, с неё и начались эксперименты с процентами. Не трогали персонажа, а только его оружие.
Дальше решила проверить статистику в другой игре этой кампании, Genshin Impact. Почти все баннеры показывали цифру в всё те же 52%. Точно такие же, как первые полгода игры Zenless Zone Zero.
То есть это политика не всей компании, а только команда разработчиков ZZZ, наёбывает игроков. Тогда как Genshin Impact, наоборот подкручивает игрокам.
UPD. Почитав комментарии, я поняла, что люди не видят, где тут обман. Поэтому решила дополнить пост, вычислениями, чтобы показать, что такие отклонения от 50% практически невозможны.
Для примера я возьму баннер персонажа Эвелин.
Для начала нам нужно количество повторений. Это кол-во S ранг сигналов и это n = 119802 (На самом деле при таких больших значениях эта цифра уже мало на что влияет, но буду максимально точна. )
Дальше нам нужно математическое ожидание. Это 50%, то есть p = 0.5.
Еще нам нужен итоговый результат. У Эвелин он равен 42.05%, то есть p^ = 0.4206
Вычисляем математическое ожидание:
μ = p * n = 119802 * 0.5 = 59901
Cтандартное отклонение:
σ = √n * p * (1 − p) = √119802 * 0.5 * 0.5 = √29950.5 ≈ 173.06
Переводим итоговую долю в количество успехов:
k = p^ * n = 0.4206 * 119802 = 50388.7 ≈ 50389
Дальше нужно использовать нормальное приближение:
z = (k - μ) / σ = (50389 - 59901) / 173.06 ≈ − 9512 / 173.06 ≈ −54.96
Я понимаю, что большенство скажет "и что это за хрень?".
Дальше мы используем таблицу стандартного нормального распределения. Для z с отрицательным значением.
https://web.crc.losrios.edu/~larsenl/ExtraMaterials/tables_Z...
И видим, что с таким значением, нас шлют в пешее эротическое, потому что, всё, что меньше -3.5, фактически равно нулю, что дальше смотреть не имеет смысла. А мы ушли ОЧЕНЬ далеко за это значение.
Для нашего примера (z ≈ −54.96) вероятность не просто "очень мала" - она ФАКТИЧЕСКИ РАВНА НУЛЮ в любом контексте.
Поэтому я делаю вывод, что игра обманывает игроков. И по другому быть просто не может.