Тригонометрия по простому⁠⁠

Тригонометрия это дисциплина, изучающая зависимости между углами и сторонами треугольников.

Она появилась как попытка найти неизвестное (расстояние, угол) имея лишь косвенные измерения.

Поэтому будут такие определения для лёгкости восприятия:

Соотношение - во сколько раз одно число больше или меньше другого числа.

Соотношение это главный ключ к пониманию тригонометрии. Скоро поймете почему.

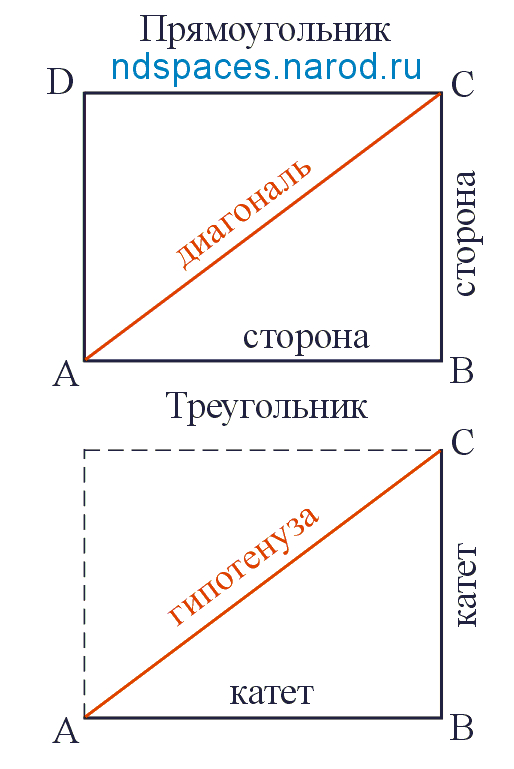
Гипотенуза - пусть будет ДИАГОНАЛЬ треугольника.

Прилежащий катет - ширина треугольника.

Противолежащий катет - высота треугольника.

Единичная окружность - просто удобный для применения МАСШТАБ.

В обозначении прямоугольных треугольников ВТОРАЯ буква всегда должна обозначать угол 90 градусов. Например буквы E и G в AED и AGF обозначают углы 90 градусов.

Все картинки делал на сайте https://www.geogebra.org/geometry/

GeoGebra для преподавания и изучения математики

Бесплатные цифровые инструменты для занятий в классе, построения графиков, геометрии, интерактивной доски для совместной работы и многого другого.

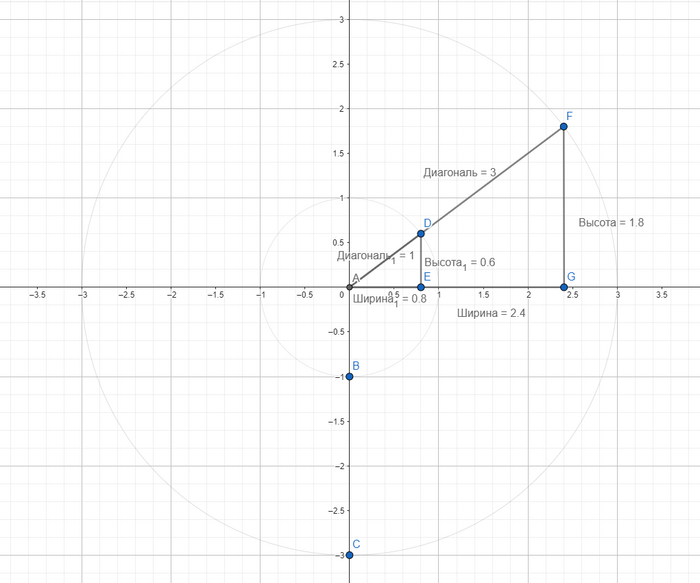
Вот два (AED и AGF) прямоугольных треугольника с разной величиной диагонали:

Если у треугольника AGF с диагональю 3, высота 1.8, а ширина 2.4, то путем деления высоты 1.8 на ширину 2.4 получаем соотношение 0.75.

Если у треугольника AED с диагональю 1 высота 0.6, а ширина 0.8, то соотношение 0.6/0.8 тоже 0.75.

Одно число больше другого в 0.75 раза. Это число называется ТАНГЕНС.

Тангенс показывает во сколько высота треугольника больше ширины. Если тангенсы треугольников одинаковы, то одинаковы и градусы углов треугольника.

Минутка заговора:

А вот функция КОТАнгенс наоборот это ширина деленная на высоту, а у мониторов соотношения сторон всегда идут как ширина деленная на высоту: 16:9 (1920x1080), 5:4 (1280х1024). А на мониторах любят сидеть КОТЫ. Вот пруфы:

И судя по всему именно коты придумали тригонометрию, а люди присвоили все лавры себе и подчинили котов. И бедным котикам приходится в знак напоминания о былом величии сидеть на геометрических предметах, мониторах и лежать коробках.

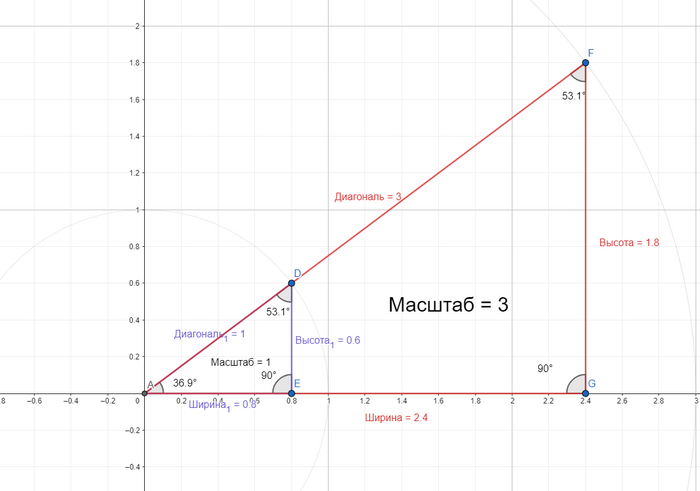
Смотрите на величины углов наших треугольников (AED и AGF) с тангенсом 0.75:

Градусы двух треугольников одинаковы, а раз эти треугольники одинаковы, судя по соотношениям сторон и углам, то можно уменьшить масштаб диагонали треугольников к единице как у AED и мы соотношений сторон и величины углов не потеряем!

Вот как и появилась единичная окружность. А масштабирование это всегда проценты.

Единичная диагональ у треугольника AED это 100%, высота 0.6 это 60% от величины диагонали, ширина 0.8 это 80% от величины диагонали.

Диагональ 3 у треугольника AGF это 300%, высота 1.8 это 180% от величины диагонали, ширина 2.4 это 240% от величины диагонали.

Просто приводим диагональ к единице и оперируем дробными значениями.

Как привести группу связанных между собой чисел к единице? Поделить каждое на самое большое из них. Самое большое у нас всегда диагональ. На него и делим.

Диагональ 3 делим на 3 и получаем 1.

Высоту 1.8 тоже делим на 3 и получаем 0.6

Ширину 2.4 тоже делим на 3 и получаем 0.8

Что такое синус?

Высота треугольника делённая на диагональ треугольника.

Синус это функция которой нужно подсунуть угол в градусах что бы получить соотношение высоты к диагонали. Диагональ в расчетах и калькуляторах и функциях всегда равняется единице (100%).

У нас левый угол A, 36.9 градусов. Нам нужно найти высоту треугольника.

sin(36.9) = 0.6 (60% от диагонали)

Высота треугольника 0.6 поделенная на диагональ 1, равна 0.6. Высота ноль целых, шесть десятых от единичной диагонали. Это просто высота треугольника указанная в десятичной дроби. А если в процентах, 60% высоты от 100% диагонали.

Дробь! Это просто десятичная дробь!

Синус это дробь которая показывает высоту треугольника по отношению к диагонали в десятичной дроби или если удобно в процентах выраженных в десятичной дроби: 0.75 это 75%, 0.23 это 23%, 1 это 100%. При единичной диагонали.

Если у нас синус угла (36.9) равен 0.6, то это значит что высота вашего треугольника 0.6 от величины диагонали 1. А как найти другие стороны? Высоту мы знаем это 0.6, диагональ у нас 1. А ширина? Тут приходит на помощь косинус.

Косинус это ширина треугольника деленная на диагональ. Что это нам дает? Подставим в косинус наш угол:

cos(36.9) = 0,8 (80% от диагонали).

Получаем ширину треугольника в десятичной дроби - 0.8 (80% от диагонали) по отношению к диагонали которая равна 1 (100%).

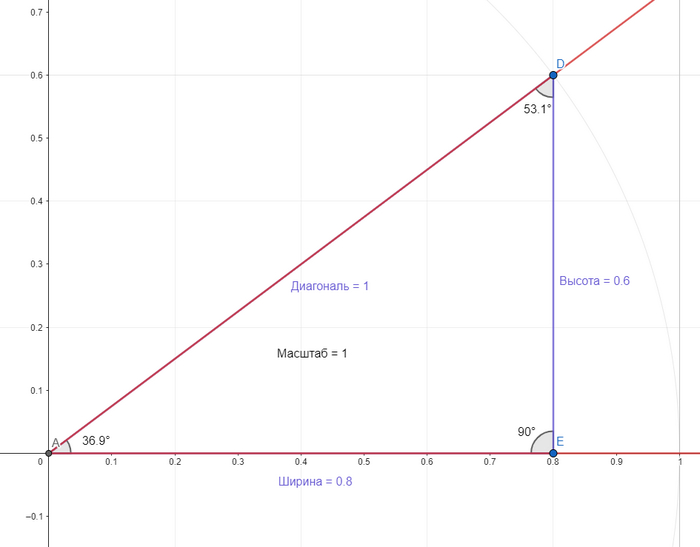
Диагональ 1, высота 0.6 от единичной диагонали, ширина 0.8 от единичной диагонали. Получаем треугольник:

Синус угла A дает нам высоту треугольника в десятичной дроби от 0.0 до 1.

Косинус угла A дает нам ширину треугольника в десятичной дроби от 0.0 до 1.

Где 0.01 это 1%, 0.3 это 30%, 0.65 это 64%, 0.8 это 80%, а 1 это 100%.