Сложность алгоритмов простыми словами⁠⁠

В программировании существует множество способов решения одной и той же задачи. Однако, не все решения одинаково эффективны. Один из ключевых аспектов, который следует учитывать при разработке алгоритмов, – это их сложность. Понимание сложности алгоритма позволяет оценить, как быстро он будет работать и сколько ресурсов (например, памяти) потребуется для его выполнения, особенно при увеличении объема входных данных. Понимание сложности алгоритмов – фундаментальный навык, который позволяет писать более эффективный код.

Что такое сложность алгоритма?

Представьте, что у вас есть задача: найти конкретное имя в телефонной книге.

• Простой способ (линейный поиск): Вы берете книгу и начинаете листать страницу за страницей, пока не найдете нужное имя. Если имя в самом конце книги, вам придется перелистать всю книгу.

• Умный способ (бинарный поиск): Вы открываете книгу посередине. Если имя, которое вы ищете, идет раньше имени на этой странице, вы закрываете вторую половину книги и ищете в первой половине. Если имя идет позже, вы ищете во второй половине. И так повторяете, пока не найдете нужное имя. При каждом шаге вы отбрасываете половину книги.

Сложность алгоритма – это способ описать, сколько "времени" (или ресурсов, например памяти) потребуется алгоритму, чтобы выполнить свою задачу, в зависимости от того, насколько "большая" эта задача.

• Линейный поиск: Если в книге 10 страниц, вам может потребоваться пролистать 10 страниц. Если в книге 100 страниц, вам может потребоваться пролистать 100 страниц. Количество работы растет линейно с размером задачи. Это называется O(n), где 'n' – это размер задачи (количество страниц в книге).

• Бинарный поиск: Если в книге 16 страниц, вам потребуется максимум 4 шага, чтобы найти имя. Если в книге 32 страницы, вам потребуется максимум 5 шагов. Количество работы растет гораздо медленнее, чем размер задачи. Это называется O(log n) (читается "о от логарифма эн").

• Алгоритм O(n) становится медленнее прямо пропорционально увеличению размера задачи.

• Алгоритм O(log n) становится медленнее гораздо медленнее, чем растет размер задачи.

Представьте, что вы разрабатываете поисковую систему. Если вы используете алгоритм O(n) для поиска в интернете (который содержит миллиарды веб-страниц), это займет невероятно много времени! А алгоритм O(log n) справится с этой задачей гораздо быстрее.

Основные типы сложности алгоритмов

Вот некоторые наиболее распространенные типы сложности:

• O(1) – Константная сложность: Время выполнения всегда одинаковое, независимо от размера задачи. Например, взять первый элемент из списка.

• O(log n) – Логарифмическая сложность: Время выполнения растет очень медленно с ростом размера задачи. Отличный пример – бинарный поиск.

• O(n) – Линейная сложность: Время выполнения растет прямо пропорционально размеру задачи. Например, пройти по каждому элементу в списке.

• O(n log n) – Линейно-логарифмическая сложность: Часто встречается в эффективных алгоритмах сортировки, таких как Merge Sort и Quick Sort.

O(n^2) – Квадратичная сложность: Время выполнения растет в квадрате от размера задачи. Например, сравнить каждый элемент в списке с каждым другим элементом в этом же списке.

• O(2^n) – Экспоненциальная сложность: Время выполнения растет очень быстро с ростом размера задачи. Обычно встречается в алгоритмах, использующих полный перебор.

• O(n!) – Факториальная сложность: Самый медленный тип сложности. Встречается при переборе всех возможных перестановок элементов.

Примеры задач и алгоритмов с разной сложностью

Рассмотрим несколько примеров задач и различных алгоритмов для их решения, чтобы увидеть, как сложность влияет на производительность.

1. Сортировка списка:

• Задача: Отсортировать список элементов в определенном порядке (например, по возрастанию).

• Алгоритмы :

  • Bubble Sort:

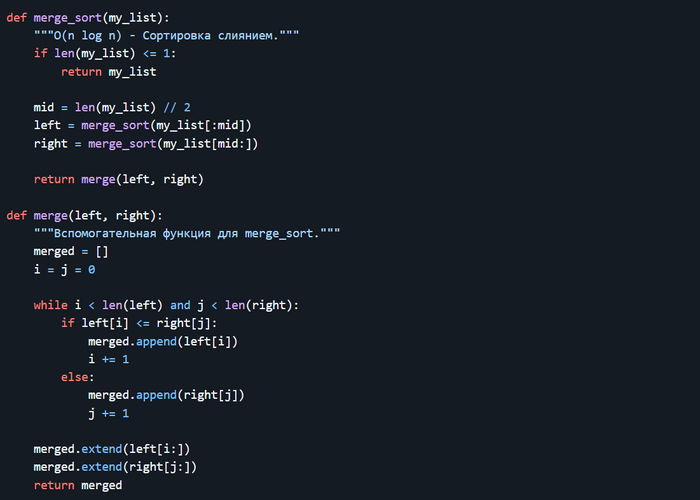
• Merge Sort:

• Вывод: Для больших списков элементов алгоритмы с O(n log n) (Merge Sort) предпочтительнее алгоритмов с O(n^2) (Bubble Sort).

2. Поиск кратчайшего пути в графе:

• Задача: Найти кратчайший путь между двумя вершинами в графе (например, между двумя городами на карте).

• Алгоритмы:

  • Алгоритм Дейкстры (Dijkstra's Algorithm):

• Вывод: Выбор алгоритма зависит от типа графа (взвешенный/невзвешенный, наличие отрицательных весов) и размера графа. Алгоритм Дейкстры эффективен для графов с неотрицательными весами.

3. Поиск подстроки в строке:

• Задача: Найти все вхождения определенной подстроки в большей строке.

• Алгоритмы:

  • Наивный поиск (Naive String Search):

• Вывод: Для частого поиска подстрок в больших строках, существуют более эффективные алгоритмы, такие как КМП.

4. Задача о рюкзаке (Knapsack Problem):

• Задача: У вас есть рюкзак определенной вместимости и набор предметов с разным весом и ценностью. Нужно выбрать предметы, которые максимизируют общую ценность, не превышая вместимость рюкзака.

• Алгоритмы:

  • Динамическое программирование (Dynamic Programming):

• Выбор алгоритма зависит от размера задачи и требований к точности решения.

O-нотация: упрощение сложности

Обычно сложность описывается с использованием "большой буквы O" (O-нотация). Она показывает, как быстро растет время выполнения алгоритма с ростом размера задачи, асимптотически, то есть для очень больших значений n. Мелкие константы и детали реализации обычно игнорируются. Например, алгоритм, который делает 2n + 5 операций, все равно считается O(n).

В худшем случае, среднем случае, лучшем случае

Сложность алгоритма может зависеть от входных данных. Обычно говорят о сложности в худшем случае – это максимальное количество времени или ресурсов, которое может потребоваться алгоритму. Иногда также анализируют сложность в среднем случае и лучшем случае.

Статья на github 👉 https://github.com/hypo69/1001-python-ru/blob/master/articles/slozhnost_algoritmov_prostymi_slovami_python/slozhnost_algoritmov_prostymi_slovami_python.md