Периодические дроби
Пост для тех, кто далек от математики или ненабаловался в своей жизни с калькулятором. Осторожно, будут цифры
Сначала вспомним, что такое периодические дроби. Наверное многие слышали "ноль целых, 56 сотых и 2 в периоде", записывается это так: 0.56(2) и означает 0.562222222222..., такого интуитивного определения нам достаточно. А теперь анекдот, который я только что придумал:
Тёплыми берлинскими вечерами Гитлер любил взять калькулятор, сесть в уютное кресло и поделить 496 на 3333В этот момент надо взять калькулятор и поделить, чтобы обнаружить
Да, наверное шутка не смешная, но она демонстрирует, что можно специально составить нужную периодическую дробь с нужным числом в периоде. Простейшие случаи многие и так должны знать наизусть 0.33333... = 1/3, 0.666666... = 2/3. Вообще говоря, для любой цифры d
Вы возможно скажете, ха, а как же d = 9. Ну-у так в математике и есть 0.99999... = 1, но сейчас не об этом. Если нам надо составить периодическое число, в периоде которого больше одной цифры, то легко проверить (на калькуляторе опять же), что работает такое правило
Ну и таки да, 1488/9999 = 496/3333, так это число в шутке и оказалось. Рецепт готов, можно пользоваться на здоровье, кому не интересно как это работает, можно скипнуть следующий раздел.
Почему это работает.
Тут достаточно показать в одном конкретном случае и все становится ясно. Применим школьный способ -- как учат восстанавливать рациональную дробь (к примеру 123/999) по периодической (0.123123...). Нужно приравнять нашу периодическую дробь к X, умножить обе части на 10^k (где k-количество цифр в периоде) тем самым сдвинув дробь влево на один период и вычесть изначальное уравнение из обеих частей. Собственно смотрим в пример с 0.(123)
Второй способ показать это же, это матан за первый курс -- нужно представить периодическую дробь в виде бесконечной суммы и выделить сумму геометрической прогрессии.
Бонус
Периодические числа в виде 0.12341234(1234)... это конечно здорово, но что если хочется представить в виде рациональной дроби число, которое вылезло при рассчетах, например на том же калькуляторе. Пускай мы что-то считали и у нас получилось число 51.525314314314... = 51.525(314), как в этом случае восстановить рациональную дробь? Школьный способ, описанный до этого, все ещё будет работать, пускай уже и не так красиво. Можно поступить проще:
Правда проще оно только тем, что тут ничего не надо запоминать, а считать уже тяжелее, собственно и мне лень досчитывать этот пример. Поэтому доработаем школьный способ, будем домножать на 10^(k+m), где k уже -- количество цифр в периоде, а m -- цифр от точки до периода, а отнимать будем 10^m, к коллайдеру примеру (а ещё мы забили болт на целую часть, потому что ну она целая, пофиг на неё)
Я специально не стал вычислять разность в числителе, чтобы рецепт стал наглядным. Мы от числа в виде части до периода и одним периодом (525314) отнимаем часть до периода (525) и делим на число, в котором подряд идёт столько 9, сколько цифр в периоде и столько нулей, сколько до периода. Пара примеров, которые можно проверять на калькуляторе чтобы убедиться:
На этом все, бесконечных BOOBS вам


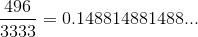
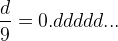
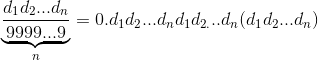

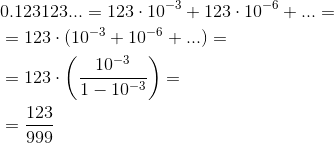
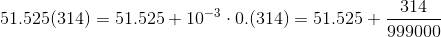
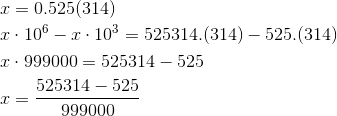
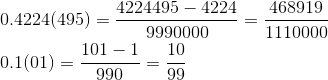
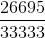
Лига математиков
916 постов2.5K подписчика