Кривизна горизонта, или что такое "Геодезическая"⁠⁠

Всем привет. Сегодня хочу рассказать вам про своё небольшое математическое исследование по мотивам блуждающих в сети вопросов о том, насколько изогнутым должен выглядеть видимый горизонт в зависимости от высоты наблюдателя над нашей планетой. По осени я рассказывал о том, как сильно должен снижаться горизонт: https://pikabu.ru/story/snizhenie_gorizonta_ili_quotna_urovn...

А сегодня мы затронем не только снижение, но и искривление видимой границы планеты. Сразу отмечу, что поскольку это качественное исследование (чтобы просто оценить масштаб трагедии), то я пренебрёг эффектами атмосферной рефракции.

В поисках терминологии, которая используется для описания искривлений, я наткнулся на интересное понятие - "геодезическая": https://ru.wikipedia.org/wiki/Геодезическая. Жаль, что прежде мне это понятие не попадалось, ведь я многократно пытался его использовать, когда задавал свою любимую загадку: "В какую сторону света нужно стартовать, чтобы кратчайшим путём долететь из Москвы в Сидней (Австралия)?" Когда люди узнавали правильный ответ (Восток), они делились на не очень грамотных (им было до лампочки, хоть на Север) и на достаточно грамотных. Последние удивлялись - при чём тут Сидней, если при движении на Восток из Москвы мы никак не попадём в Южное полушарие. И когда я им пытался объяснить, что такое движение по Большому Кругу (ортодромия), и заодно употреблял слово "прямо", они неизменно возражали, мол, прямо - это по касательной в космос. Тогда мне приходилось делать всё новые и новые оговорки - прямо в том смысле что не влево и не вправо, а высота над планетой не меняется. Всё это звучит довольно коряво, я и сам это понимал, но ничего с этим сделать не мог.

И никто не воскликнул - так ты пытаешься сказать про геодезическую линию! Поэтому я теперь восклицаю вам, товарищи: геодезическая - это и есть обобщение понятия "прямая" для искривлённых пространств, в частности для сферы - это кратчайшая дуга Большого Круга между двумя точками сферы.

Продолжая копать тему, я обнаружил геодезическую кривизну, которая характеризует, насколько вы путешествуете "не прямо". Поскольку размерность кривизны (в системе СИ - рад/м) учитывает линейные масштабы, то удобно обезразмерить кривизну - отнести к радиусу вашего искривлённого пространства. В случае Земли - к радиусу планеты 6371 км.

Давайте рассмотрим несколько значений относительной кривизны:

1) при движении по Экватору кривизна равна нулю, поскольку Экватор - это один из Больших Кругов планеты;

2) если вы двигаетесь по параллели 1 градус северной широты, то формально это уже не Большой Круг, но очевидно, что отличается от Большого круга он очень незначительно, поэтому кривизна хоть и ненулевая, но около того: 0.017;

3) при движении по 45-й параллели относительная кривизна вашего путешествия равна единице - это означает, что радиус вашего поворота (влево или вправо) равен радиусу планеты;

4) при движении по 89-й параллели вы двигаетесь почти по плоскому кругу радиусом 111 км, и кривизна при этом составляет 57.

Вы спросите - какое отношение всё это имеет к кривизне горизонта? Самое непосредственное. Дело в том, что когда вы находитесь на высоте 1 километр, и снижение горизонта составляет минус 1 градус, то горизонт искривлён настолько же, насколько искривлена параллель 1 градус северной/южной широты, если бы её можно было наблюдать из центра Земли. Поскольку геометрия в обоих случаях одинакова. Больше того - ровно то же самое можно применить к кривизне звёздных треков на небосклоне - чем дальше звезда от небесного экватора (чем больше склонение по абсолютной величине), тем большую кривизну имеет её траектория на небосклоне. В частности для Солнца: в дни равноденствия траектория Солнца имеет кривизну = 0, а в дни солнцестояния (склонение плюс-минус 23.4 градуса) кривизна составляет 0.43. А Полярная Звезда в нашу эпоху крутится с кривизной траектории около 80. А кривизна края лунного диска в среднем составляет около 220.

Я решил пойти дальше и визуализировать эти искривления, чтобы своими глазами понять, как именно должен выглядеть идеальный горизонт с разной высоты. Пришлось учитывать два следующих нюанса:

1) поскольку кривизна с малых высот очень мала, то для отрисовки пришлось использовать гауссово размытие линии, чтобы линия не прыгала с пикселя на пиксель, создавая грубое изображение;

2) поскольку вы рассматриваете изображение на экране определённого размера, то вообще-то воспринимаемая кривизна будет зависеть от того, с какого расстояния вы смотрите на экран.

Для преодоления последней сложности в верхней части рисунка я включил масштабный отрезок, равный 1/10 от расстояния, с которого вам нужно смотреть на рисунок. Вот буквально - открываете картинку, измеряете масштабный отрезок линейкой, умножаете на 10, и располагаете лицо от экрана на этом расстоянии. Скажем, если масштабный отрезок равен 5 см, то наблюдать картинку нужно с 50 см.

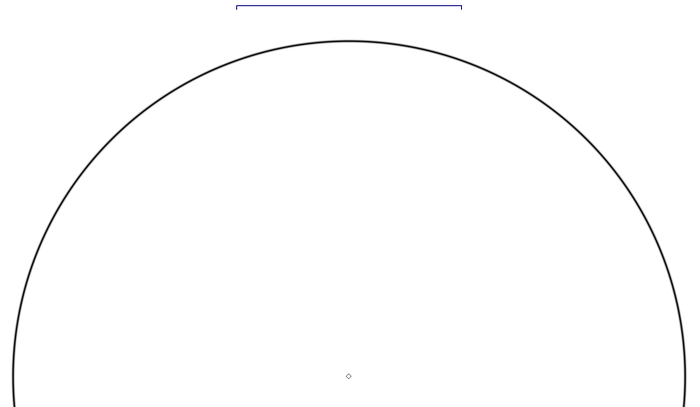
Ну и наконец несколько картинок, ради которых было написан весь текст выше. Первая - это искривление горизонта на стандартной "самолётной" высоте 12 км (помните про масштабный отрезок):

Вот об эту кривизну в интернетах сломано много копий. Кто-то утверждает, что видит эту кривизну. Кто-то - что не видит. Видите ли вы сами эту кривизну? Мне кажется, что я вижу. )

Тут есть ещё один момент. Дело в том, что при наблюдении горизонта из самолёта сам горизонт зачастую скрыт облаками, которые доходят до высот около 10 км. Иными словами, если вы летите на высоте 11 км, а сплошная облачность доходит скажем до 9 км, то вы фактически наблюдаете горизонт с высоты 11-9 = 2 км. Конечно, и кривизна при этом получается весьма сомнительной (не говоря про размытость), и снижение горизонта - заметно меньше ожидаемого.

На следующей картинке представлены 11 линий - обобщение для снижения горизонта от 0 градусов (наблюдение с поверхности планеты) до 10 градусов (высота почти 100 км, это Линия Кармана, которая считается границей атмосферы и космоса, а заодно - верхней границей государств). Каждая линия подписана, но едва заметным шрифтом (чтобы не мешать восприятию самих линий):

По вертикали линии расположены в соответствии со снижением горизонта - то есть именно так будет снижаться видимый горизонт (относительно математического) при увеличении вашей высоты над планетой. Посмотрите на них: как вам кажется, на какой высоте вы гарантированно увидите изгиб? )

В заключение пара картинок с характерных высот.

Снижение 19 градусов, высота 370 км (примерно как с МКС):

Снижение 81.5 градуса (если его так можно назвать для таких больших высот), высота 37000 км (примерно геостационарная орбита):