Как определить угловой размер в компьютерных играх
Всем доброго времени суток
Когда возникает желание что-то посчитать в игре, то нередко приходится определять размеры объектов по их изображению, то есть иметь дело с угловыми размерами объектов. Например, есть за картой звездолет и хочется узнать, насколько он большой. Для этого как раз нужно в том числе и определять его угловой размер. Что это такое и как его найти и будет рассказано в этом посте
Что такое угловой размер
Угловой размер - это мера того, насколько большим мы видим объект. И пожалуй объясню это на примере
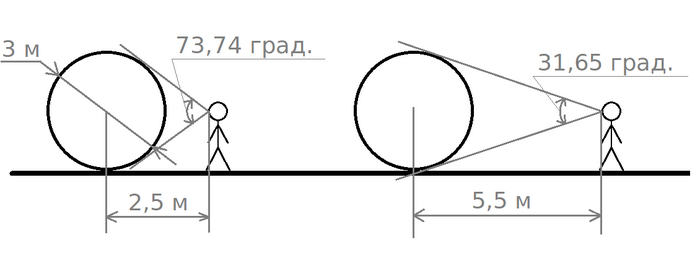
Представьте, что вы стоите напротив шара диаметром 3 метра и смотрите на него. Сперва вы смотрите на него с расстояния в 1 метр, затем отходите подальше и смотрите уже с 4 метров. Сам шар размеры свои не изменил, однако для вас он стал меньше, потому что вы удалились. И вот как раз то, насколько большим вы его видите, угловой размер и показывает:
Естественно, угловой размер связан не с самим шаром, а с диаметром круга, который мы видим (изображение шара для глаза - это круг). Ну то есть в общем случае он связан с отрезком, который видит человек, камера или персонаж в игре
Как строится изображение
Предупреждение: так как я не занимаюсь разработкой видеоигр, то могу не могу быть полностью уверен в данной математической модели. Если она ошибочна в общем случае, то прошу указать об этом в комментариях
Спроецируем все объекты, которые мы можем увидеть из некоторой точки на какую-то поверхность. Вот только на какую? Так как по любому направлению проецироваться объекты должны одинаково, то очевидным будет сделать проекцию на сферу, в центре которой находится наблюдатель. На этой сфере находятся все объекты, которые может увидеть наблюдатель, изменяя только направление своего взгляда. Естественно, из-за ограниченного угла обзора наблюдатель видит только часть этой сферы
Однако мониторы прямоугольные и, в основном, плоские, поэтому теперь видимый кусок сферы нужно спроецировать на прямоугольник. Отсечем от сферы те части, которые наблюдатель не видит, а из концов отрезанного куска проведем прямые, пересекающиеся в центре. На этих отрезках и будет лежать прямоугольник, и для удобства его можно построить прямо на концах куска сферы:
Зеленая плоскость - это как раз плоскость монитора
И теперь, чтобы спроецировать некоторую точку на плоскость монитора, проведем прямую от этой точки на сфере до центра сферы. Точка пересечения с плоскостью и будет проекцией точки на эту плоскость. Кстати, такой метод проецирования объясняет, почему по краям изображение растягивается
Находим угловые размеры
Пусть есть какой-то отрезок, который находится в поле зрения наблюдателя. Проведем прямые из концов этого отрезка в центр сферы. Угол между прямыми как раз и будет угловым размером этого отрезка. Теперь пересекаем эти прямые с плоскостью монитора и получаем концы отрезка уже на изображении. И теперь, если нам известны точки, которыми отрезок ограничен, то мы можем определить угловой размер. Как это сделать?
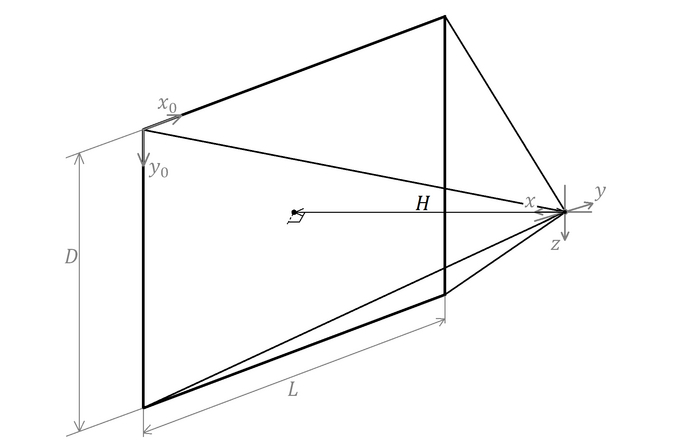
Сперва введем 2 системы координат: одна 3-мерная, из центра сферы, другая 2-мерная, связанная с плоскостью монитора:
Здесь L - длина изображения в пикселях, D - высота, что, впрочем, видно и по рисунку. Также здесь у нас появилась неизвестная H, которую надо бы найти. Рассекаем объекты с рисунка плоскостью xOy и, соединяя с началом координат края сечения монитора получим следующую картину:
Так как начало координат находится ровно над центром монитора, то мы получаем равнобедренный треугольник. Теперь можем из FOV-а (угла обзора) и длины изображения выразить неизвестную:
Изначально мы будем знать координаты точки в системе координат монитора (например, координата пикселя в Paint-е), поэтому из них определим координаты уже в системе Oxyz для некоторой точки:
Не забываем, что Oxyz находится над центром монитора
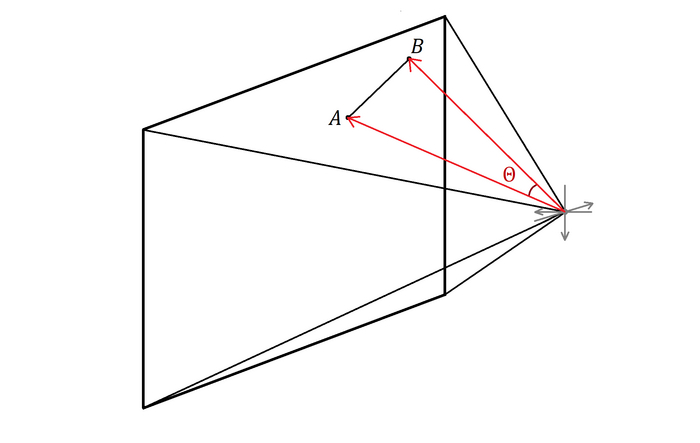
Теперь вернемся к исходной картинке, нанесем на плоскость точки A и B, которые будут границами нашего отрезка и проведем вектора из наблюдателя (нуля Oxyz) в эти точки:
Напомню, что эти векторы лежат на прямых, угол между которыми нужно найти. А значит нужно найти угол между векторами. Тут же напрашивается скалярное произведение этих векторов, поэтому не будем изобретать велосипед и воспользуемся им:
Вторая картинка - та же формула, но с записью обозначений, чтобы ее можно было сохранить и потом быстро ею воспользоваться
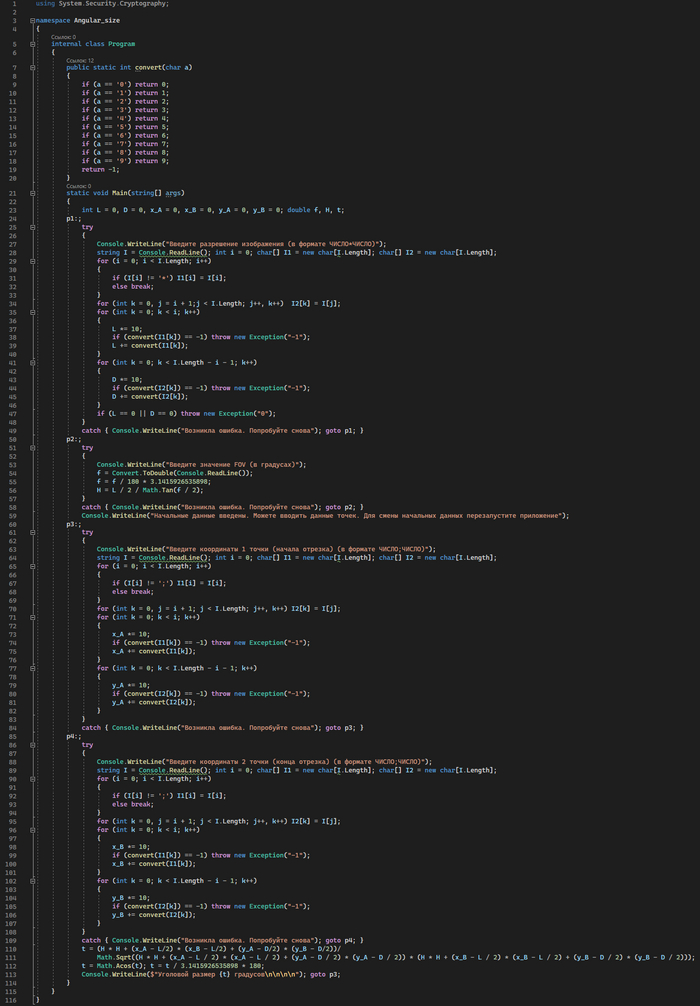
Ну и что ж, вот конечная формула. Определяем координаты пикселей, разрешение и угол обзора, подставляем в формулу и получаем угловой размер. Однако такая формула выглядит довольно громоздко, поэтому я решил написать небольшую консольную программу, которая сможет считать угловые размеры. Оставлю здесь ссылку для скачивания на Яндекс диск, а также код самой программы, вдруг кто захочет разобраться в ней:
Ну а на этом все, удачи вам в расчетах и вычислениях)


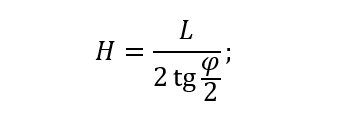
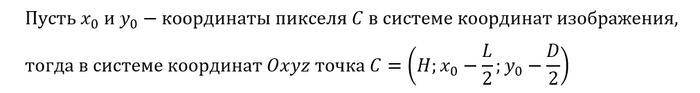
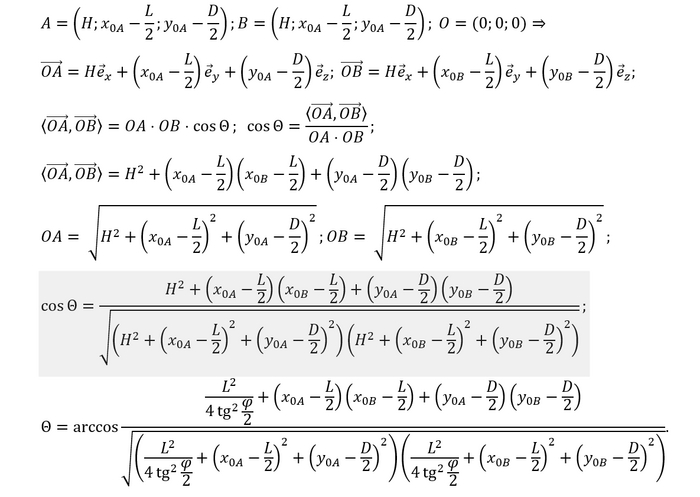

Лига упоротых расчетов
495 постов7K подписчиков
Правила сообщества
Лига занимается странными веселыми подсчетами на основании уже имеющихся в общем информационном доступе знаний. Расчеты - ради лулзов и хорошего настроения. Не нудите сами и не занудничайте в адрес других, играть в Шелдона Купера хорошо до определенного предела.