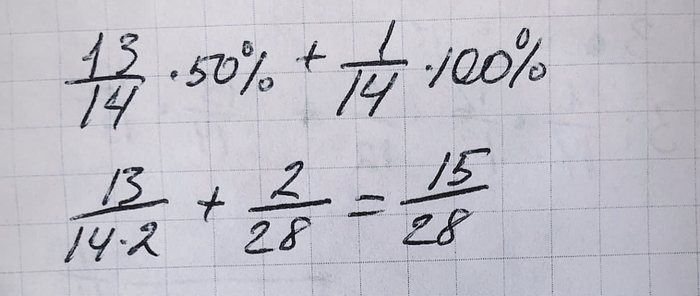Задача Пуаро (теория вероятности)⁠⁠

Убийство в “Восточном Экспрессе”. Версия для полиции.

В вагоне 14 мест, один пассажир потерял билет и выбирает купе случайным образом, другие 13 человек занимают свои места. Но если место занято, то пассажир выбирает другое свободное.

Последним в поезд входит Джонни Депп.

Его хотят убить. Незнакомец (15ый пассажир) пробирается в вагон и протыкает того, кто спит в купе Джонни.

Какова вероятность, что это будет он, а не другой пассажир?

Пассажир, потерявший билет, был СЛУЧАЙНЫМ (может быть и Джонни), он выбирает новое место в вагоне СЛУЧАЙНО. Другие пассажиры, если их место уже занято,  выбирают новое место тоже СЛУЧАЙНО.

Решение.

Задачу я придумала, опираясь на оригинал про безумную старушку и самолёт. Ее мне загадали однажды 2 программиста, когда я была совсем далека от программирования (привет Косте и Серёже).

Итак, я немного изменила условия, что повлияет на результат (если мои рассуждения верны). Но начало решения общее.

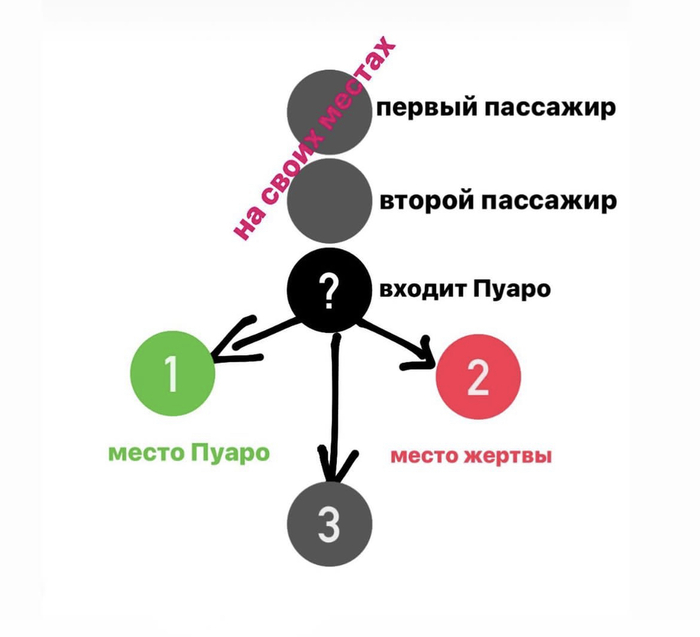
Пассажиры занимают свои места. Никаких других вариантов развития событий нет, пока в поезд не заходит пассажир без билета. Назовём его Пуаро.

Пуаро может:

— занять своё место, тогда все займут места согласно билетам, а Джонни убьют.

— занять место жертвы и тогда убьют Пуаро.

— занять чьё-то ещё место.

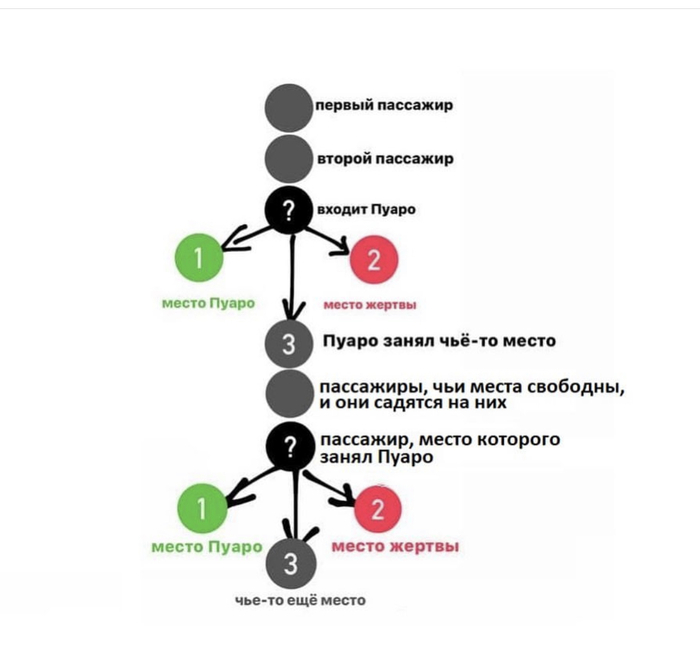
Следующий пассажир, чьё место занято, занимает:

1) место Пуаро.

2) место Джонни Деппа.

3) чьё-то чужое.

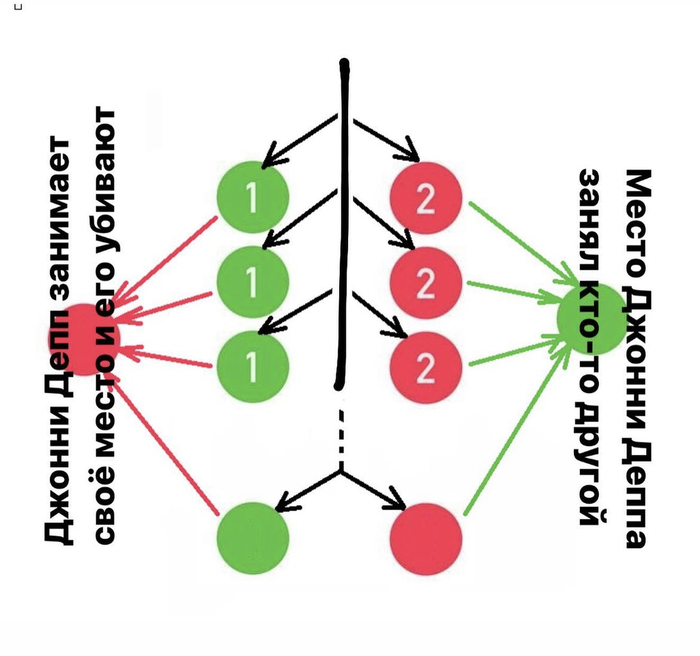
Вероятность (1) и (2) одинаковы. Вероятность (3) повыше, но это не важно, тк в случае (3) места Пуаро и жертвы остаются свободными, игра продолжается.

Если пассажир, на чьё место сели, займёт место Пуаро, порядок восстановится, оставшиеся пассажиры будут занимать свои места, и Джонни убьют.

Если пассажир, на чьё место сели, займёт место Джонни, убьют этого пассажира.

Предпоследний пассажир #13 (если до него никто так и не сел ни на место жертвы, ни на место Пуаро) выбирает одно из этих мест. И таким образом решает, кто умрет. 50 на 50.

Получается, что вероятность того, что на место Джонни Деппа сядет кто-то другой - 50%.

Но пассажиром без билета может быть и сам Джонни (в 1 случае из 14). И тогда все остальные пассажиры занимают свои места, а его со 100% вероятностью убивают.

Джонни без билета - квази Пуаро в вакууме.

То есть в 13 из 14 случаев его убьют с вероятностью 50%. И в 1 из 14 - 100%.

Вероятность Джонни быть убитым 15/28 или 54%.