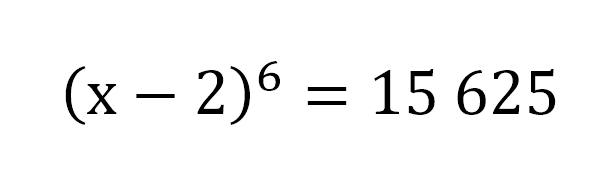Олимпиадная задача⁠⁠

Олимпиадная задача для 11(?) класса, но это не точно.

Нужно найти все корни, в комплексных числах.

Не очень сложная, но корней должно быть 6.

Ход решения:

Принимаем t = (x-2). Учитывая, что t^6 = (t^3)^2, а так же формулы разности квадратов и суммы и разности кубов получаем (t-5)(t^2 + 5*t + 25)(t+5)(t^2 - 5*t + 25) = 0. Тут уже легко, находим 6 значений t, из них 6 значений x.