Камень-ножницы-бумага
Попробуем найти равновесие в смешанных стратегиях для игры «камень-ножницы-бумага».
Напомним правила данной игры :
Ножницы режут бумагу,
Камень ломает ножницы,
Бумага покрывает камень.
Эта игра действительно проста и хорошо известна. Например, ей смогли научить нескольких шимпанзе (пантроглодитов). Это забавное исследование было проведено китайскими и японскими исследователями на 7 животных (3 молодых и 4 пожилых) из Института исследований приматов Киотского университета (Япония). Ученые смогли объяснить нашим «родственникам» правила игры, а затем приматы должны были выбрать правильный ход на сенсорном экране, чтобы выиграть игру. По результатам исследования, представленным в 2017 г. в научной статье, 5 из 7 шимпанзе успешно завершили обучение, продемонстрировав тем самым свое владение правилами этой игры. Ученые не обнаружили никаких зависимостей результатов от возраста или пола этих животных.
В 2013 году в Японии сконструировали робота, который со стопроцентным успехом побеждает человека в «камень-ножницы-бумага». Выигрыш получается не за счет конкретной стратегии, а за счет анализа движений руки человека с помощью высокоскоростной камеры. Но как найти баланс в игре между двумя людьми?
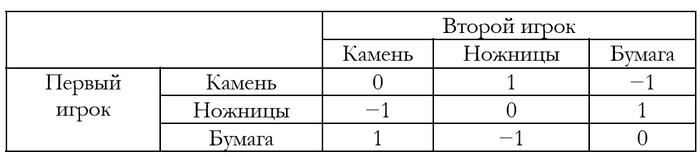
Построим платёжную матрицу для данной игры. Это игра с нулевой суммой, в которой «1» – это победа, «-1» – поражение, «0» – ничья.
Пусть первый игрок выбирает камень с вероятностью x, ножницы с вероятностью y и бумагу с вероятностью 1−x−y.
Тогда математическое ожидание выигрыша второго игрока в случае выбора им камня будет равно 0∙x+(-1)∙y+1∙(1-x-y).
В случае выбора ножниц это математическое ожидание будет равно
1∙x+0∙y+(-1)∙(1-x-y), а в случае выбора бумаги будет равно (-1)∙x+1∙y+0∙(1-x-y).
Тогда равенство потенциальных доходов можно записать в виде:
0∙x+(-1)∙y+1∙(1-x-y)=1∙x+0∙y+(-1)∙(1-x-y)= (-1)∙x+1∙y+0∙(1-x-y).
Решив систему двух уравнений с двумя неизвестными, находим, что в равновесии наш ожидаемый выигрыш будет равен 0 и достигается, когда y = x = 1/3.
Аналогично можно определить и оптимальную стратегию для второго игрока. Логично, что в этой симметричной игре она такая же, как и у первого игрока.
На самом деле, «игра в монетку» и игра в «камень-ножницы-бумагу» весьма специфичны. Лучшей стратегией, как мы уже поняли, является случайный равновероятный выбор одного из вариантов. Но тогда средним выигрышем будет 0!.. Как же тогда существуют чемпионы по данным играм? Это просто лотерея или что-то большее? Почему они так популярны? На самом деле, данные игры весьма психологичны, так как, что ни говори, всё равно оба игрока будут пытаться предсказать ход противника.
Самая крупная сумма, выигранная в этих играх, составляет 50 тысяч долларов. Его выиграл в Лас-Вегасе Шон Сирс, который не собирался участвовать в тот вечер в игре «камень-ножницы-бумага». Но он неожиданно обыграл за вечер 300 противников и заслужил прозвище «сумасшедшие пальцы». Сирс объяснял свой успех умением наблюдать за противником в конкретной ситуации и не придерживаться одной тактики.