Задача о трисекции угла из новости⁠⁠

Ответ на пост

Было время, когда я тоже жил в Миассе и занимался школьной математикой, весьма неплохо, надо сказать. Поэтому мимо такого поста я не мог пройти. Так бомбануло, что не дочитал, и стал писать ответный с телефона.

Честно говоря, никогда не слышал про эту женщину, пока учился. Но это неважно.

Что важно - это безграмотность журналистов, или кто там текст писал. Статья написана в стиле "срыва покровов": бедную женщину все выпинывают, не хотят даже ковыряться в решении, а ее нужно номинировать на нобелевку.

Даже не смотря на доказательство, уже хочется закрыть статью. Начнем с того, что Нобелевки по математике нет и никогда не было. Продолжим тем, что учительница на пенсии могла потерять хватку в математике, и если она не показала свои результаты коллегам прежде, чем бегать по верхушкам математического мира, то могла упустить существенные вещи. А сильным математикам обычно интересны вопросы посложнее школьной математики, и не надо их винить, что им не очень-то интересна школьная и давно разобранная задача. Закончим отвратительной подачей, которая НАМЕКАЕТ, что здесь МОЖЕТ БЫТЬ что-то интересное, а ученые СКРЫВАЮТ ПРАВДУ, потому что они погрязли в своей теореме невозможности, а она имеет НЕЗАШОРЕННЫЙ ОТКРЫТЫЙ К НОВОМУ УМ. А, ну и ДЕТИ СЕЙЧАС ТУПЫЕ.

Ну что же. Пошевелим остатками мат. знаний в голове и разберём, в чем же проблема. Как по мне, ее мог бы понять любой хороший школьник.

Простейший метод доказательства - пример. И никаких компьютеров не надо, как некоторые уже начали делать. Пишу с телефона, поэтому визуализируйте на листочке.

(Здесь начинается скучная часть)

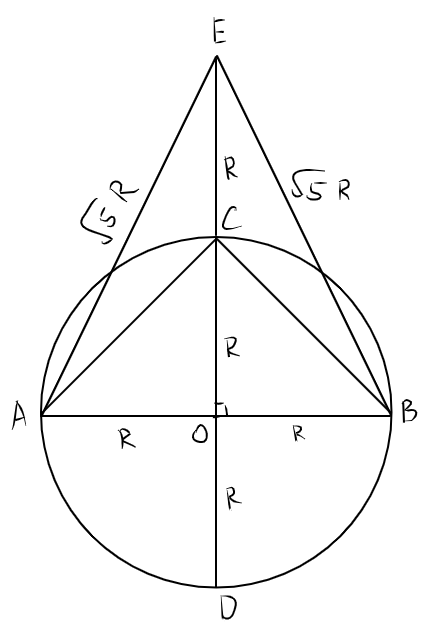
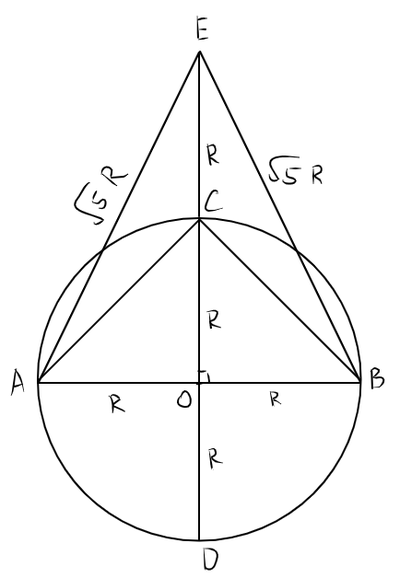
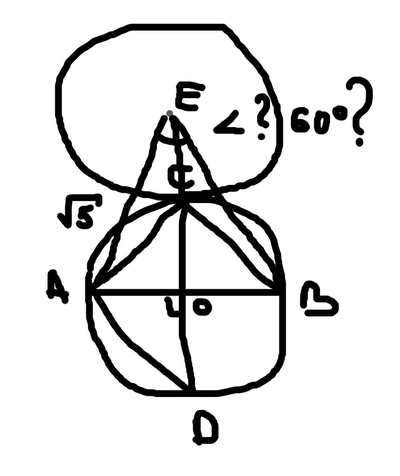
Итак, берём окружность с центром О. Строим горизонтальный диаметр АВ. Угол АОВ - развернутый, то есть, равен 180 градусов. Трисекция предполагает разбиение на углы по 60 градусов. Итак, строим диаметр CD, перпендикулярный первому. Угол ACB - прямой (вписанный угол равен половине центрального - школьная теорема, есть даже в ЕГЭ), причем СО - биссектриса. На продолжении СО отложим ещё один радиус EC. Получили треугольник АЕВ, угол которого должен быть 60 градусов, да? По построению АЕВ - равносторонний. Но АЕ=ЕВ= корень из 5 радиусов (теорема Пифагора, тоже школьная), АВ - диаметр и равен 2 радиуса. Противоречие.

Почему пенсионерке могло показаться, что она нашла решение? Банальная математическая проблема - неудачный пример.

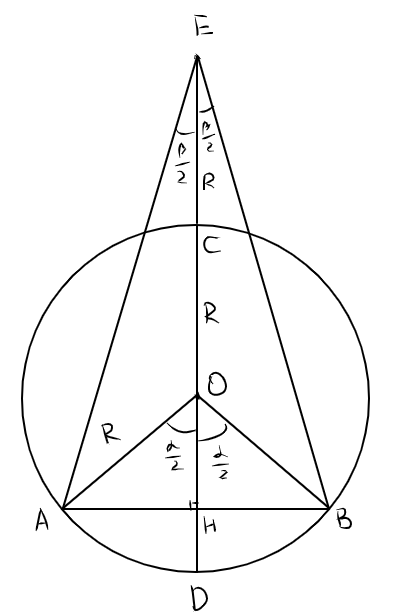
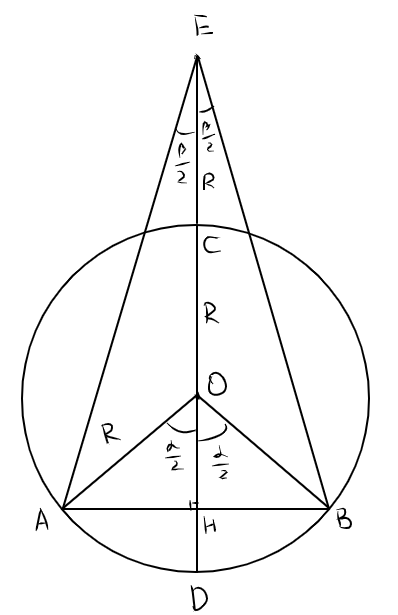
Попробуем решить в общем виде. Возьмем произвольную хорду АВ окружности, получим произвольный центральный угол АОВ. Построим перпендикулярный диаметр CD и назовем точку пересечения АВ и CD как Н. На продолжении CD отложим радиус ЕС. Угол АЕВ есть два угла АЕН. Пусть заданный угол АОВ равен а, а радиус - р. Тогда тангенс АЕН равен р*sin(a/2)/(2р+р*cos (a/2)) =sin (a/2)/(2+cos (a/2))=tg(a/2)*[cos (a/2)/(2+cos(a/2))]

Копаем глубже: приближенные вычисления для получившегося числа. cos (a/2) приближается к 1 при малых углах. Значит, дробь в квадратных скобках ПРИБЛИЖАЕТСЯ к 1/3. При малых углах (обычно меньше 10 градусов) тангенс ПРИМЕРНО равен самому углу (здесь необходимо уточнить, что это только для углов в радианах, но сути не меняет.). Значит, выражение дает нам ПРИМЕРНО а/6, если считать в радианах. Тогда угол АЕВ ПРИМЕРНО равен а/3, и погрешность тем меньше, чем меньше взят угол.

Понимаете? ВИЗУАЛЬНО эффект будет хороший даже для достаточно больших углов. Я провел вычисления для угла а=60 градусов (примерно тот, что у женщины на картинке) и получил угол при "трисекции", равный 19.79 градусов. Это очень близко к предполагаемым 20.

*****

Какой можно сделать вывод? Если вы нашли простой способ решения нерешенной проблемы - вероятно, он не работает. Десятки людей до вас шли тем же путем, вы вряд ли уникум. Научитесь нормально проверять решение, включая крайние случаи, и тогда одной теорией заговора наверняка станет меньше.