Форма Земли, или что такое геоид
Всем привет. Из дискуссий о форме Земли я часто замечаю, что люди знают слово геоид, но зачастую не представляют, что именно это слово означает. Хочу тезисно осветить тему.
В середине 1730-х из Парижа отправляют две экспедиции, одну к экватору (в Перу), другую к полярному кругу (в Лапландию). Цель экспедиций - определить, насколько сильно Земля отличается от шара, а также - в какую именно сторону (по расчётам Ньютона выходило, что Земля должна быть слегка сплюснута с полюсов, а Кассини такого намерил вблизи Парижа, что Земля у него выходила вообще вытянутой). Выясняли это при помощи максимально точных на тот момент измерений длины дуги меридиана, соответствующей одному градусу. [1] В случае сплюснутой Земли длина одноградусной дуги меридиана должна удлиняться при перемещении от экватора к полюсу. Именно это и было надёжно подтверждено. Это было первое в истории человеческого знания отклонение фигуры Земли от шара - в сторону слегка сплюснутого эллипсоида вращения (сфероида). [2]
В последующие века геодезия (наука о фигуре Земли) продолжала развиваться, а с появлением космических аппаратов в 20 веке появилась и спутниковая геодезия, с помощью которой удалось дополнительно уточнить параметры фигуры Земли.
В качестве системы описания параметров Земли используется WGS 84 или её российский аналог ПЗ-90. В качестве отсчётного тела используется общеземной эллипсоид вращения с большой полуосью (то есть средним экваториальным радиусом) 6378 км и сжатием эллипсоида 1/298. [3]
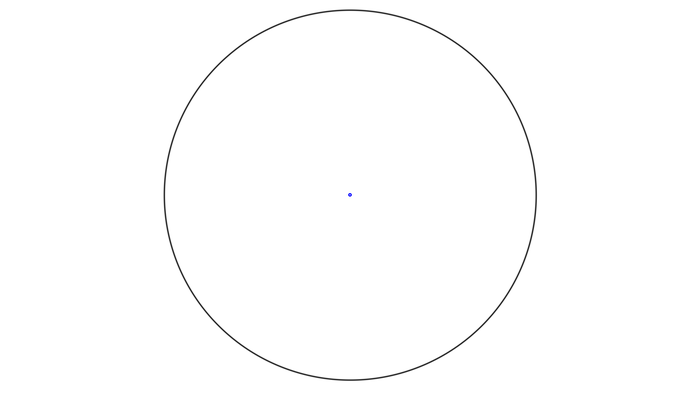
Сразу обращаю внимание на малую величину сжатия эллипсоида - разница полярного и экваториального радиусов, несмотря на её на первый взгляд заметную абсолютную величину (21 км), составляет всего 1/298, то есть 0.3%. Чтобы наглядно увидеть, насколько это малая сплюснутость, нарисуем Землю в разрезе по (любому) меридиану:
Например сверху Северный полюс, снизу Южный, вращаем этот эллипс вокруг оси, проходящей через полюса, и получаем общеземной эллипсоид вращения. Внимание, вопрос: видите ли вы отличие этого эллипса от окружности? Вряд ли. Поэтому если вы упоминаете сплюснутость Земли сами или слышите о сплюснутости от другого человека, вспоминайте эту картинку.
Как следствие, форма Земли настолько незначительно отличается от шара, что упоминать про её сплюснутость во многих случаях - излишняя академичность. В большинстве "бытовых" расчётов (если вы, скажем, захотите посчитать расстояние между двумя точками с заданными координатами) вам будет достаточно первого приближения фигуры Земли - шар с радиусом 6371 км (при этом точность расчёта расстояния окажется в среднем не хуже 0.5%).
В некоторых сетевых дискуссиях люди меня уверяли, что если фигура хоть сколько-то отличается от шара, то это уже не шар. Вот такая, понимаете ли, принципиальность. Мои попытки рассказать этим людям, что идеальных геометрических фигур в физической реальности не существует, были не очень успешны. И когда я демонстрировал вышеприведённую картинку и спрашивал, чем же она так отличается от окружности, мне либо говорили, что я рисую вообще что-то не то, либо разводили руками.
Из вышесказанного вы уже понимаете, что вторым приближением к форме Земли является общеземной эллипсоид вращения (с вышеуказанными величинами большой полуоси и сжатия). Если представить себе Землю без суши, с ровным дном и без неоднородных вкраплений (плотные породы и тому подобное), то форма Земли (а именно поверхность мирового океана) с хорошей точностью совпадала бы с эллипсоидом вращения.
К слову, эллипсоид вращения и образовался как раз из-за суточного вращения нашей планеты, и когда возникает вопрос "почему нет горба воды в районе экватора из-за вращения", я отвечаю, что "горб" как раз есть, но он размазан между экватором и полюсом. Сумма гравитационной и центробежной сил как раз и дают направление силы тяжести (локальной вертикали), которая практически перпендикулярна к нашему эллипсоиду.
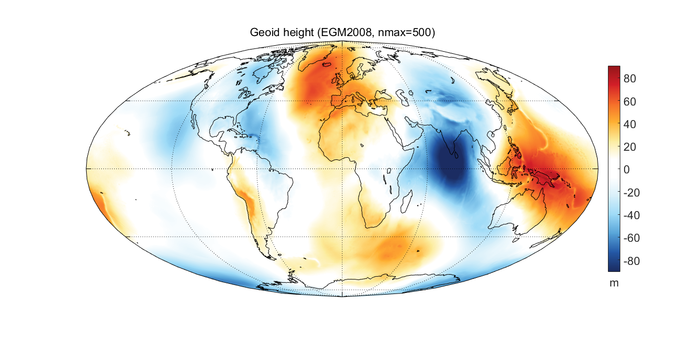
Практически перпендикулярна, однако в следующем, третьем приближении, есть отклонения направления силы тяжести (называется уклонением отвеса), связанные с неоднородностями: неровная поверхность суши и дна водоёмов, а также неравномерное распределение плотностей во внутренней структуре Земли. Это приводит к тому, что реальная поверхность мирового океана отличается от эллипсоида на величины до 100 метров. Такая уровенная поверхность невозмущённой поверхности мирового океана, причём продолженная под континентами, и называется геоидом. [4]
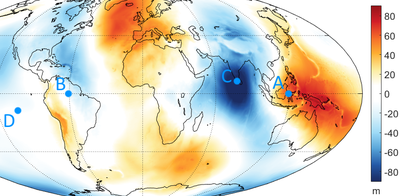
Так выглядит карта высот геоида относительно эллипсоида:
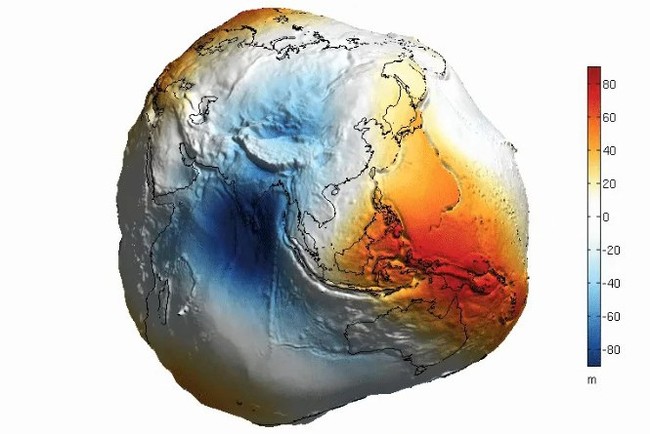
Понятно, что если на глаз трудно отличить даже 20-километровую сплюснутость Земли (эллипсоид в сравнении с шаром), то отличия геоида от эллипсоида в десятки метров в масштабе были бы тем более незаметны. Поэтому для целей визуализации отличий геоида от эллипсоида (не от шара, подчёркиваю) была сделана картинка, в которой эти отличия были утрированы на несколько порядков. А затем эту картинку кто-то вбросил со словами "так выглядит Земля без воды!" И почему-то этот вброс в своё время приобрёл вирусный характер, и до сих пор многие так и продолжают считать, что это форма Земли без воды:
Думаю, многие из вас неоднократно видели эту картинку. Удивительно, как широко может распространиться квази-знание о такой форме Земли, и как мало тех, кто радостно постит это художество, задумываются, почему в легенде указаны такие малые величины - десятки метров.
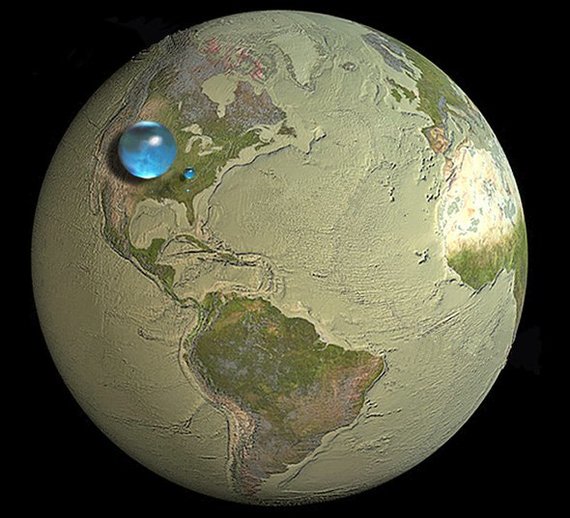
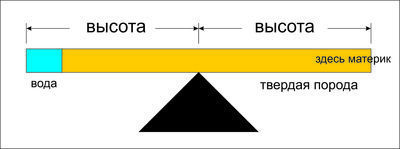
На самом деле Земля без воды будет выглядеть примерно так (шарики воды в порядке убывания - вся солёная вода; вся пресная грунтовая вода; вся пресная вода в открытых водоёмах):
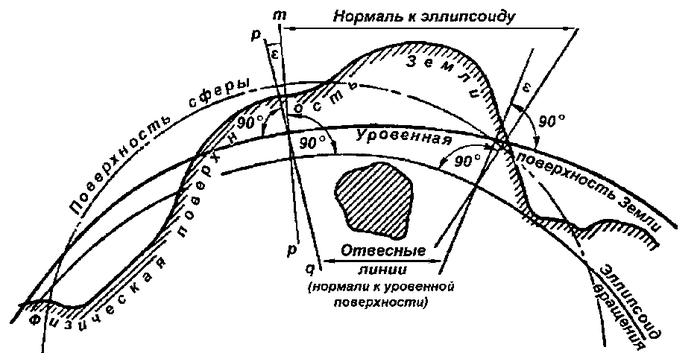
Ну и завершим мы такой, например, вполне подходящей картинкой, на которой не в масштабе, а условно приведены разные поверхности всех трёх приближений к форме Земли (сфера, эллипсоид вращения, геоид):
Отметим, что уровенных поверхностей может быть много, на разных высотах, и только одна уровенная поверхность называется геоидом - та, которая совпадает с поверхностью мирового океана. Ваша высота над уровнем моря, которую вам показывает барометр и GPS, - это высота относительно геоида. Поэтому ответ на мой "каверзный" вопрос (который я иногда задаю тем, кто любит упоминать слово геоид), входит ли Эверест в форму геоида - нет конечно, не входит. Его высота 8848 метров именно относительно геоида и приводится.
Примечания.
[1] Эти измерения проводили с помощью триангуляционной разметки на Земле и последующих астрономических измерений высоты кульминации выбранной звезды.
[2] Слова "форма" и "фигура" в данном тексте - равноправные синонимы.
[3] Приведённые значения округлены, более точные значения составляют 6378136 метров и 1/298.258.
[4] Невозмущённая - без волн и без приливных эффектов. Уровенная поверхность - поверхность, при перемещении по которой работа силы тяжести равна нулю.

Исследователи космоса
19.6K постов49.3K подписчиков
Правила сообщества
Какие тут могут быть правила, кроме правил установленных самим пикабу :)