Теорема о рычаге (геометрия масс)
НИГДЕ НЕ НАШЕЛ УПОМИНАНИЯ ЭТОЙ ТЕОРЕМЫ, ПОЭТОМУ НАПИСАЛ ЭТОТ ПОСТ
Пусть заданы точки x1, x2, x3... xn с приписанными им числами (массами) m1, m2... mn. Тогда точка O будет центом масс системы, если выполняется следующее равенство (определение центра масс):
(такая точка всегда существует, причем только одна)
Теорема о рычаге
Пусть заданы точки A и B, в точке А лежит груз массой а, а в точке B лежит груз массой b.
Пусть О - центр масс системы, тогда справедливо следующее утверждение: AO = αb, BO = αa.
Очевидно, что точка О лежит на отрезке AB.
Доказательство:
По определению центра масс:
Поскольку векторы OA и BO лежат на одной прямой, то справедливо будет сделать переход к следующему равенству:
Отсюда собственно и следует равенство: AO/BO = b/a. Теорема о рычаге доказана!
Мне часто пишут, что я не умею заинтересовать народ, т.е. написал про что то, а где применять не показал... хорошо, давайте при помощи теоремы о рычаге докажем, что в треугольнике медианы пересекаются в одной точке (центр масс треугольника) и делятся в отношении 2:1 считая от вершины.
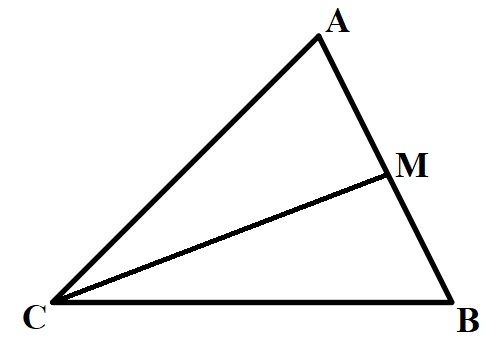
Пусть CM - медиана треугольника ABC. Положим в каждую вершину треугольника по грузу массой 1 грамм. Тогда точка M - центр масс AB, т.е. если мы груз из точек А и В положим в точку М, то центр масс треугольника останется на своем месте. Теперь в точке М лежит 2 грамма, а в точках A и В ничего не лежит, очевидно, что центр масс CM будет центром масс треугольника ABC. По теореме о рычаге получаем, что точка O (центр масс) должна делить отрезок CM в отношении 2:1 считая от вершины.
Аналогично делаем для других медиан. Очевидно, что центр масс для треугольника ABC один, значит все медианы пересекаются в центре масс и делятся точкой пересечения в отношении 2:1 считая от вершины. ДОКАЗАНО.
Ну а теперь решение задач из планиметрии!
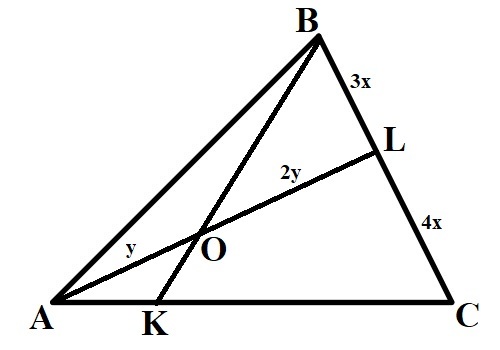
В треугольнике ABC точка L делит сторону BC в отношении 3:4 считая от точки B. На прямой L взяли точку O такую, что AO/OL = 1/2. Через точки B и О проводят прямую, которая пересекает сторону АС в точке K. Найти: AK/KC и BO/OK.
Решение:
Необходимо положить некоторую массу в вершины треугольника, что бы точка О стала центром масс треугольника. Сделаем L центром масс отрезка ВС, из теоремы о рычаге следует, что для этого нужно положить в точку В 4 грамма, а в точку С 3 грамма. Теперь необходимо сделать точку О центром масс отрезка AL, из теоремы о рычаге следует, что в точку А нужно положить 14 грамм.
Теперь, после того как мы положили в вершины A, B и С по 14г, 4г и 3г соответственно точка O стала центром масс треугольника ABC.
Найдем отношение AK/KC. Заметим, что K - центр масс AC, поскольку центр масс всего треугольника - точка О, лежащая на BK. Если бы центр масс АС был в точке M (M ≠ K), то центр масс треугольника ABC должен быть на BM, что не есть возможным, поскольку M ≠ K.
И опять таки из теоремы о рычаге следует, что AK/KC = 3/14.
Аналогично можно доказать, что О - центр масс BK, и опять теорема о рычаге... BO/OK = 17/4.
А теперь самое интересное! При помощи теоремы о рычаге можно найти центр масс тетраэдра и доказать, что медианы тетраэдра пересекаются в одной точке и делятся в отношении 3:1 считая от вершины.
Def: Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противолежащей грани.
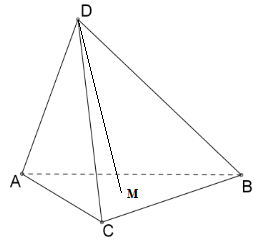
Пусть M - точка пересечения медиан треугольника ABC, тогда DM - медиана тетраэдра.
Положим в каждую вершину 1 грамм, тогда M - центр масс треугольника ABC, из теоремы о рычаге следует, что центр масс должен делить отрезок DM в отношении 3:1 считая от вершины. Аналогично для других медиан, а поскольку центр масс один, то все медианы тетраэдра пересекаются в центре масс тетраэдра и делятся в отношении 3:1 считая от вершины.

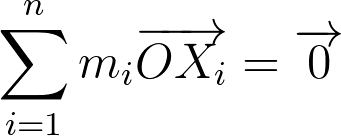

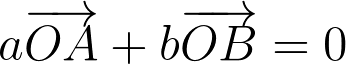
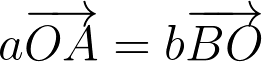
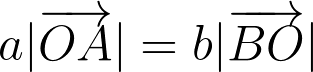
Лига образования
6.7K постов22.9K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
ДЛЯ АВТОРОВ:
Приветствуются:
-уважение к читателю и открытость
-желание учиться
Не рекомендуются:
-публикация недостоверной информации
ДЛЯ ЧИТАТЕЛЕЙ:
Приветствуются:
-конструктивные дискуссии на тему постов
Не рекомендуются:
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
В этом сообществе мы все союзники - мы все хотим учиться! :)