Кых⁠⁠

Ну ИИ какую-то фигню может выдавать, как в этом случае, ему не нужно слепо верить

Если просто взять треугольник удовлетворяющий условию x^n + y^n = z^n, и посчитать чему равно m в данном случае, то оно не будет равно n, примеры посчитаны ниже

Я не опровергаю теорему, я беру нецелое z, явно считаю косинус угла и показываю, что при таких значениях x, y, z которые удовлетворяют x^n + y^n = z^n, значение m не равно n, тем самым показываю ошибку в доказательстве

в другой ветке явно взят треугольник, удовлетвроряющий x^n + y^n = z^n и показано, что значение m в нем не равно n

я не беру целое z, я беру точное значение z, которое равно в первом случае кубический корень из (x^3 + y^3) = кубический корень из (1+8), то есть кубический корень из 9, который естественно не целый

во втором случае беру соответственно значение (2^4 + 3^4)^(1/4) = 97^(1/4), опять же не целое число, никаких приближений я не беру

ну и что

для 2 работает, для остальных N>=3 не работает

я брал не 3, а кубический корень из 9, 1^3 + 2^3 = (9^(1/3))^3, так что тут проблем нет, и m и n оказались не равны

ну допустим, возьмем 2^4 + 3^4 = z^4, как ты предлагаешь, тогда z = 97^(1/4)

cos(a) = (x^2 + y^2 - z^2) / 2xy = (4 + 9 - sqrt(97)/(2 * 2 * 3) = (13 - sqrt(97)) / 12

Тогда 1 - cos(a) = (sqrt(97) - 1) / 12

Тогда если m = n = 1/4, то 2^(1/4) = sqrt(2) * sqrt (sqrt(97) - 1) / sqrt (12)

Опять же легко проверить, что равенство неверно, то есть m не равно 4

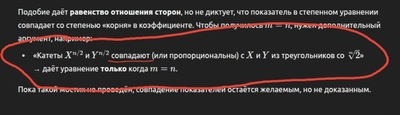
Ошибка вот в чем: по теореме косинусов следует, что a = x * sqrt(2) * sqrt (1 - cos(a)), где a - угол между x и y, вы это приравниваете числу x * 2^(1/m) при некотором m и утверждаете, что m должно быть больше 2

Но при этом число 1 - cos(a) может быть равно 1, если угол а прямой или даже больше 1, если угол а тупой, так что 1-cos(a) лежит на интервале (0; 2), а значит, m не обязано быть больше 2, оно может быть равно 2 (если угол а прямой) или даже меньше 2, при прямоугольном треугольнике m = 2 как раз число (2^(1/2))^2 получается рациональным

Далее если 1 - cos(a) < 1/2, то есть при угле меньше 60 градусов, получается, что 2^(1/m) = sqrt(2) * sqrt (1 - cos(a)) < sqrt(2) * sqrt (1/2) = 1, то есть 2^(1/m) меньше 0, а значит и m может быть меньше 0

К тому же m совсем не обязательно целое, так что финальный шаг с иррациональностью 2^(2/m) тоже не работает, например, m = 2 / (log_2(3) - 1), тогда 2^(2/m) = 1,5 и может быть любым рациональным на интервале (1; 2), например если оно равно 41/30 x = 5, y =6, получается z^2 = 25 + 36 + 30 * 41/30 - 2 = 100, то есть треугольник x = 5, y = 6, z = 10 подходит под ваше итоговое выражение (но не под теорему ферма)

Более того ваше доказательство нигде не использует условие x^n + y^n = z^n, то есть оно запрещает в целом треугольники, у которых все стороны целые, хотя такие треугольники очевидно есть

так, из чего следует, что m = n, это как раз вообще не очевидно сходу, можете вывести это?

P.S. Более того это неверный факт

Вы утверждаете, что m = n

Рассмотрим треугольник, удовлетворяющий x^3 + y^3 = z^3 со сторонами x = 1, y = 2 и z =cbrt(9), в нем n = 3, (cbrt - кубический корень)

тогда m - решение уравнения 2^(1/m) = sqrt(2) * sqrt ( 1 - cos(a)), где cos(a) находится из теоремы косинусов:

По теореме косинусов x^2 + y^2 - 2xy*cos(a) = z^2, откуда cos(a) = (x^2 + y^2 - z^2) / (2xy), cos(a) = (5 - cbrt(81))/4, значит 2^(1/m) = sqrt(2) * sqrt (81^(1/3) - 1) / 2

Если m = n, то m = 3, а значит cbrt(2) = sqrt(2) * sqrt(cbrt(81) - 1) / 2, что неверно

Так что m не равно n

Предположим, доказали для таких целых чисел x, y, z, из которых можно собрать треугольник.

А если взять целые x, y, z для которых так сделать нельзя? Например, x = 2, y = 3, z = 10. x и y слишком коротки чтобы замкнуть концы отрезка z.

Можно с первых строк сказать что оно неверно, так как теорему ферма нельзя доказать только евклидовой геометрией

Почему пост на Пикабу, а не в рецензируемом научном журнале?

Можно с первых строк сказать что оно неверно, так как теорему ферма нельзя доказать только евклидовой геометрией