Айсберг больших чисел. Часть 3.2. Дно айсберга (продолжение)
В первой части этого поста мы начали говорить о быстрорастущей иерархии функций и дошли до функции
Эта функция растет настолько быстро, что даже сама математика в каком-то смысле не может осознать эту скорость. Поясню.
Каждая математическая теория начинается с системы аксиом — очевидных истин, которые принимаются "на веру". Вот пример такой системы аксиом в арифметике натуральных чисел — аксиомы Пеано.
Аксиома 1. Существует число, назовем его "1".
Аксиома 2. К любому числу можно прибавить 1 и получить другое число.
Аксиома 3. Нет такого числа, к которому можно прибавить 1 и получить 1. (То есть в этой системе аксиом единица — это первое по порядку число, нуля нет)
Аксиома 4. Если a + 1 = b + 1, то a = b.
Аксиома 5. Если какая-то формула F верна для единицы, а также верно утверждение: "Если формула F верна для n, то она верна и для n+1", то эта формула верна для всех чисел. (Это аксиома математической индукции (погуглите), и если вы не поняли, что здесь написано, не парьтесь.)
Из этих аксиом можно вывести почти все вам известные факты о натуральных числах. Например:
От перемены мест слагаемых сумма не меняется;
От перемены мест множителей произведение не меняется;
Простых чисел бесконечно много;
Между n и 2n обязательно есть простое число;
И множество других теорем, более сложных в доказательстве.
Но некоторые факты нельзя доказать, используя только аксиомы Пеано. И такие факты часто используют функции, растущие также или быстрее, чем
Один из таким фактов — Теорема Гудстейна. (Разбор теоремы на Youtube, 4.5 часа)
Для начала возьмем любое натуральное число и запишем его, как сумму степеней двойки:
Это всегда можно сделать, на этом вообще основана двоичная система счисления. (Вспомните школьный курс информатики).
В числе 2^3 в показателе осталась тройка, и мы можем разложить её также.
Мы получили запись числа 9 в так называемой "наследственной нотации" (англ. "Hereditary base-n notation" по основанию 2.
Теперь механически меняем все двойки в этой записи на тройки и отнимаем в конце единицу.
Переписываем получившиеся число в наследственной нотации по основанию 3. Для этого представляем число в троичной системе счисления, все цифры в этом числе умножаем на соответствующие степени тройки. (Опять же, вспомните системы счисления!). То же повторяем для показателей степеней, пока в итоге не останется чисел, больших 3.
Меняем теперь в этом числе все тройки на четверки и отнимаем в конце единицу. Получившееся число переписываем в наследственной нотации по основанию 4, меняем все 4 на 5 и отнимаем единицу, и так далее, и так далее.
Теорема Гудстейна утверждает, что в конце этой последовательности получится ноль. Кажется абсолютно контринтуитивным, но это так. Последовательность поначалу стремительно растет, но в какой-то момент очередной член последовательности приходит к виду
в наследственной нотации по основанию B, после чего начинает уменьшаться.
Так вот, длина этой последовательности для числа n растет примерно как
что "слишком быстро" для системы аксиом Пеано.
Конечно, математики не ограничиваются системой аксиом Пеано. В системе аксиом Цермело-Френкеля (сейчас неважно, что это за система) теорему Гудстейна доказать можно.
Но ведь быстрорастущая иерархия не заканчивается! Вот примеры, которые я объяснять уже не буду:
И так далее, и тому подобное. Где-то в этом списке есть и еще одно известное число TREE(3), его масштаб строго не доказан, но оценивается, как
И, честно говоря, даже я так глубоко в это не погружался и не отвечу, что все эти греческие буквы означают. Да и это, вообще говоря, уже не имеет значения, так как ничего принципиально нового здесь нет — это всё также рекурсия и диагонализация, погруженные в другие слои рекурсии и диагонализации, погруженные в другие слои ре...
Тем не менее, у математиков нашелся способ строить еще большие числа, но о нём в следующей статье.

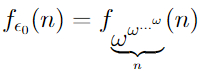
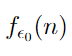
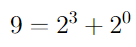
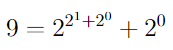
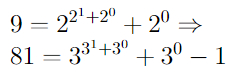
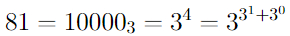
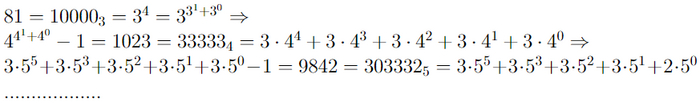
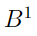
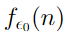

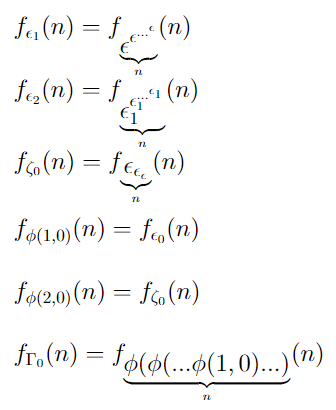
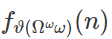

Наука | Научпоп
9.4K поста82.8K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.