Айсберг больших чисел. Часть 2. Подводное течение
Не думал, что напишу вторую часть на следующий же день. Но таки вот, держите)
В прошлом посте мы рассмотрели те числа, которым можно найти хоть какое-то применение на практике. То, что будет дальше, вам в жизни не пригодится и скорее определяется как своеобразная форма искусства. Это искусство может поразить не меньше «Моны Лизы» или «Черного квадрата», и вызвать эмоций больше, чем музыка Pink Floyd.
По теме дам еще пару ссылок. Для разнообразия.
Сегодня мы поговорим о гипероператорах и попробуем понять определение (не само число!) числа Грэма. Чтобы начать погружаться в эти пучины безумия, нам нужно систематизировать кое-какие школьные знания.
Как и в прошлый раз, вам понадобится знание математики на уровне 7-8 класса, воображение и немного абстрактного мышления.
Начнем с самой простой операции — операции сложения двух чисел, или, на языке гугологии — гипероператора первого порядка. Чтобы понять, что будет дальше, нам нужно определить сложение, как итерированное (повторённое) прибавление к числу единички, например:
Здесь число под фигурной скобкой означает количество повторений. Вроде бы понятно.
Соответсвенно, каждый следующий гипероператор определяется как итерированное применение предыдущего. Вот пример для умножения — ведь это повторенное несколько раз сложение!
Стоит заметить, что умножение, как гипероператор 2 порядка, уже действует намного эффективнее. Сравните, например, числа 10 + 20 и 10*20 — разница уже почти на порядок.
Следующий гипероператор — возведение в степень, определяется (как бы вы думали?), через повторенное умножение!
И здесь мы уже улетаем в стратосферу. Вспомните, что числа из первого поста мы определяли именно через степени, а они уже не вмещались в нашу Вселенную!
Но что насчет следующего гипероператора? В школе о нем не говорят, да и в универе вроде не проходят. Дело в том, что тетрация растет настолько быстро, что почти ни в одной из задач, не созданных специально, её нельзя применить!
Записывать тетрацию, как «башню степеней», несколько неудобно, поэтому стоит познакомиться с альтернативной формой записи гипероператоров — стрелочной нотацией Кнута. Возведение в степень в этой форме записывается вот так:
А тетрация — вот так:
Стоит заметить, что на этом этапе математика уже начинает потихоньку ломаться, и результат тетрации будет зависеть от того, как расставить скобки. Например:
Как видно в примере, если вычислять выражение сверху вниз, результат получится больше. Математики делают именно так.
Чтобы понять масштаб чисел, попробуем что-нибудь посчитать:
В этом числе уже содержится 65536 цифр!
Ну а в числе 2↑↑6 количество цифр будет равно 2↑↑5.
В числе 2↑↑7 количество цифр будет равно 2↑↑6, и.т.д.
(Примечание: Количество цифр в двоичной записи. В десятичной записи цифр будет примерно в 3 раза меньше, что не имеет особого значения на таких масштабах).
Уже 2↑↑6 нельзя записать в обычном десятичном виде, даже если мы бы могли записать цифру в каждом атоме вещества во вселенной. Даже если бы в каждом атоме во Вселенной содержалась целая мини-вселенная, мы бы не смогли записать и толику цифр этого числа на всех атомах мини-вселенной в каждом атоме нашей вселенной. Чтобы все-таки это сделать, уровень вложенности этих мини-вселенных должен быть равен примерно 250. Хотя, признаюсь честно, мог ошибиться. Разбор в комментариях приветсвую)
Повторюсь — это все про число 2↑↑6, а уже в числе 2↑↑7 количество цифр равно 2↑↑6, и.т.д.
(Картинка для стимуляции воображения™ )
А ведь это только тетрация — четвертый по счету гипероператор.
Пентация, гексация, и последующие гипероператоры в нотации Кнута записываются аналогично предыдущим — количество стрелок на 2 меньше порядка гипероператора.
Вот пентация:
И гексация:
Не забываем, что вычислять нужно справа налево!
Слишком много стрелочек писать долго, поэтому n-тацию сократим следующим образом:
Хоть как-то осознать масштаб пентации еще можно, так что приведу пример.
Вспомните тетрацию: количество цифр в числе 3↑↑7625597484987 равно числу 3↑↑(7625597484987 - 1). Дальше думайте сами, а я себя лучше пожалею.
Теперь мы готовы, чтобы поговорить о числе Грэма.
В свое время его записали в книгу рекордов Гиннесса, как «самое большое число, когда-либо участвовавшее в серьезном математическом доказательстве». Сейчас это уже не так, но об этом в следующей части.
Число Грэма — оценка числа измерений пространства (обозначим, как N), при котором начинает выполняться некоторое комбинаторное свойство N-мерного гиперкуба. Если вы когда-то пытались представить 4 измерения, и вас не получилось — даже не пытайтесь представить пространство с числом Грэма измерений. Не получится.
(воображение уже не поможет, задействуйте абстрактное мышление™)
Не получится и определить его напрямую через нотацию Кнута, но можно итеративно. (Вспомните, как мы в начале поста определили сложение). Поехали.
Первое число в последовательности — g(1), определим как
Уже g(1) находится вне досягаемости в принципе чего угодно. Следующее — g(2), уже нельзя определить через нотацию Кнута напрямую, ведь количество стрелочек уже равно g(1).
В числе g(3) уже g(2) стрелочек, в g(4) — g(3) стрелочек, и.т.д. Число Грэма — это 64 число в последовательности, то есть g(64).
(картинка из википедии)
Не имеет смысла писать, насколько это много.
Поэтому скажу только, что в терминах быстрорастущей иерархии последовательность g(n) примерно порядка
и это только самое начало. Но об этом в следующий раз. Ждите через пару недель.


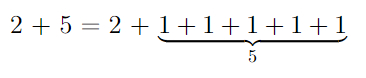
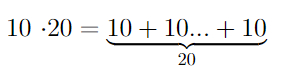
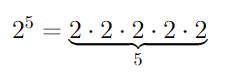
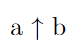
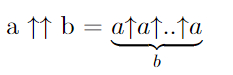
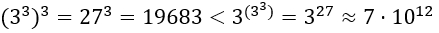
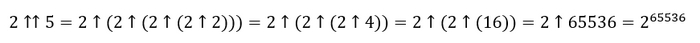

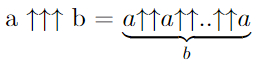
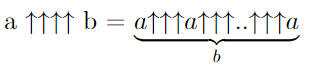
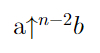
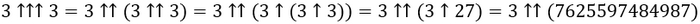
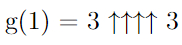
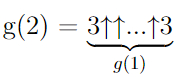

Наука | Научпоп
9.4K постов83K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.