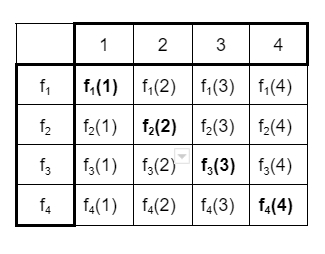
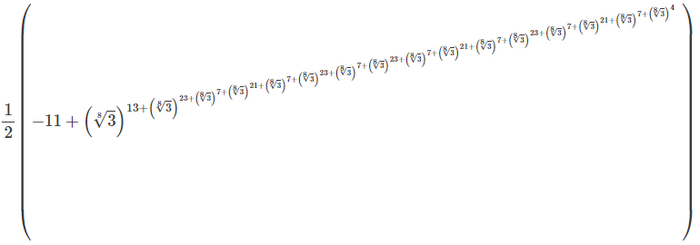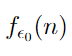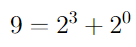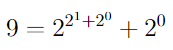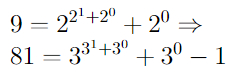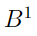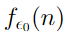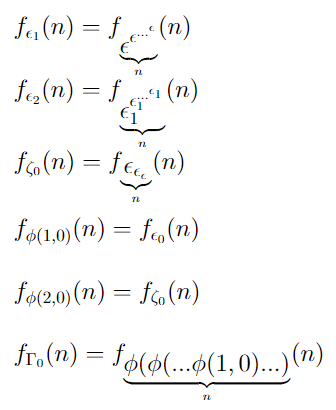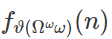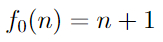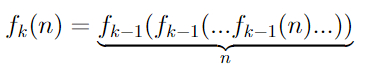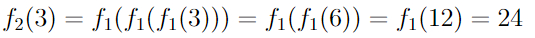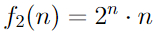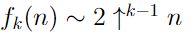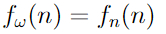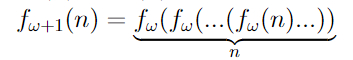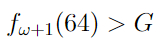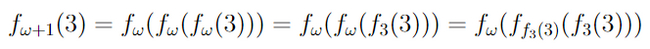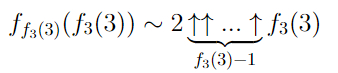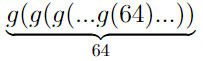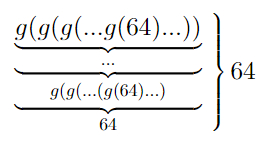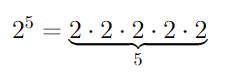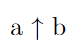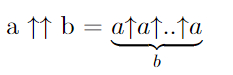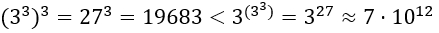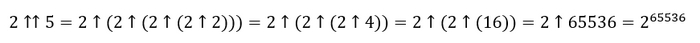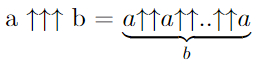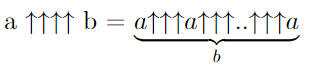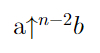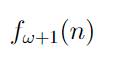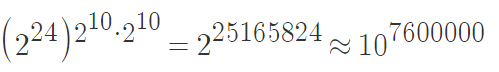Серия «Айсберг больших чисел»

Парадокс этот скорее шутливый, но у него есть и более серьезный аналог (парадокс Берри):

Теорема: Все натуральные числа можно описать, используя менее 10 слов.

Доказательство: Пусть существуют числа, которые нельзя никак описать менее, чем за десять словам. Выберем из всех этих чисел минимальное. Теперь опишем его, как "Наименьшее число, которое нельзя описать, используя менее 10 слов". В этом описании содержится 9 слов. Отсюда противоречие, а значит все числа можно описать менее, чем за 10 слов.

В чем же подвох?

(Сможет ли Уроборос сожрать себя целиком?)

Все эти парадоксы эксплуатируют один и тот же прием — самореференцию, или ссылку на самого себя. В простейшем виде самореференция выглядит так:
"Это предложение ложно". Если оно ложно, значит в нем говорится истина, но если оно истинно, значит оно ложно. Но ведь мы уже сказали, что оно не может быть ложным, потому что в этом случае оно было бы истинным, но в этом случае оно ложно, но...

В математике самореференция, если она приводит к парадоксу, означает, что что-то не так с предпосылками. В примере с "интересными" числами такой предпосылкой было утверждение, что принадлежность числа к "неинтересным" или "интересным" сама по себе может быть интересна. Второй пример чуть сложнее, но и там тоже все это есть — нельзя при описании числа использовать ссылку на само это описание числа. Получается порочный круг, деление на ноль, Марти Макфлай встретился сам с собой, а оба близнеца оказались старше друг друга.

Мы используем этот тип парадоксов, чтобы доказать существование невычислимых функций, то есть таких, для которых не существует хоть какого-то общего способа или алгоритма, их вычисляющего.
Вообще вычислить можно почти что угодно. Все те монстры от мира функций, о которых мы говорили в предыдущей статье (быстрорастущая иерархия) вычислимы, ведь их можно посчитать на каком-то вычислительном устройстве. Конечно, на обычном компьютере или тем более в уме сделать это невозможно. Важна лишь потенциальная возможность, лишь бы в вашем компьютере была неограниченная память и в вашем распоряжении имелось неограниченное время. (Заметьте, не бесконечность в прямом смысле, здесь и сейчас, а именно неограниченность!)

Чтобы наконец рассмотреть понятие вычислимости, надо как-то его формально определить. Для этого Алан Тьюринг придумал абстрактную машину, названную потом его именем — машину Тьюринга.

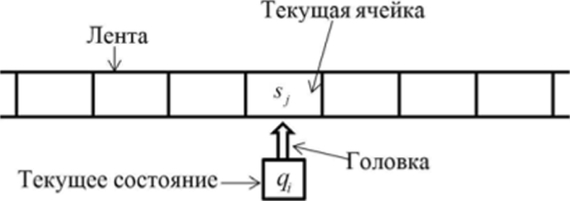
(картинка из интернета для наглядности)

Машина Тьюринга состоит из трех элементов — неограниченной в обе стороны ленты, разделенной на ячейки, считывающего устройства (головки), и набора правил, по которым машина, собственно, и работает.
В ячейках ленты изначально находятся какие-то символы (входные данные), а головка может находиться в одном из нескольких состояний. Правила описывают, что делать машине в случае, если головка находится в таком-то состоянии и находится напротив ячейки с таким-то символом. А может эта машина за один раз:

1. Записать в ячейку напротив головки некий символ (другой или такой же)

2. Сдвинуть головку на одну ячейку вправо или влево

3. Поменять состояние головки (на какое-то другое или оставить его тем же)

4. Остановить машину.

Вот пример правил для машины с двумя состояниями головки и двумя возможными символами в ячейке ленты:

1. Если головка находится в состоянии А, а в ячейке записан символ "0", записать в неё "1", сместить головку вправо и поменять её состояние на B.

2. Если головка находится в состоянии А, а в ячейке записан символ "1", сместить головку влево и оставить состояние А.

3. Если головка находится в состоянии B, а в ячейке записан символ "0", сместить головку влево и оставить состояние B.

4. Если головка находится в состоянии B, а в ячейке записан символ "1", записать в неё "0", сместить головку вправо и остановить машину.

Поиграться можно, например, здесь.

Сейчас мы не будем углубляться в эту тему, скажу лишь, что что на машине Тьюринга можно эмулировать любой алгоритм, который можно написать и на обычном языке программирования. Берите любой: Python, Java, C++ — эта грубая и уродливая машина Тьюринга справится с чем угодно. И вообще, в дальнейшем мы будем использовать термин "программа", а не "машина Тьюринга". (Но не забывайтесь, машины Тьюринга нам еще понадобятся).

Но есть одна задача, для которой силы машины Тьюринга не хватает — так называемая "проблема остановки". Решить проблему остановки — означает написать программу, которая узнает, остановится ли когда-нибудь данная конкретная программа или нет. (Чувствуете запах самореференции?)

Вроде бы очевидно, что проблема остановки разрешима: нужно лишь проверить, зацикливается ли программа в каком-то месте. Ну а если в правилах для этой машины вообще нет правила для её остановки, то очевидно, что она не остановится.

Но всё не так просто и вот пример. Возьмите какую-нибудь нерешенную до сих пор гипотезу для натуральных чисел, например, проблему Гольдбаха. (Её математики уже почти 300 лет решают!). Запустите программу, которая для каждого натурального числа проверяет, выполняется ли условие задачи. Если для очередного числа условие не выполняется, остановите программу. Математики за 300 лет не узнали, есть ли такое число, и у вас вряд ли выйдет.

На самом деле не существует такого алгоритма S, которому на вход подавалась бы запись любого другого алгоритма A, а на выходе он бы отвечал, останавливается ли A или нет.

Доказательство:

Пусть существует программа S, на вход которой подается запись любой программы A и входных данных к A, а на выходе она решает проблему остановки для программы A при этих входных данных: например — печатает одно из двух: "Программа останавливается" или "Программа не останавливается".

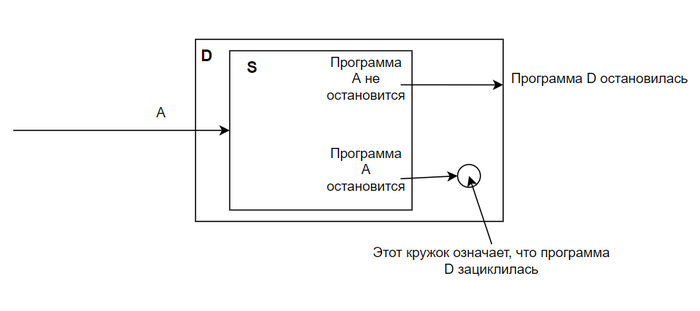
Напишем программу D, которая принимает на вход запись любой программы A и входных данных к A, выполняет внутри себя программу S, и, если S печатает "Программа останавливается", то D не останавливается (зацикливается), а если S печатает "Программа не останавливается", то D останавливается.

Подадим теперь на вход программы S запись программы D и любого входа к ней A. Если D останавливается, то S должна вывести, что D не останавливается, но если D не останавливается, то S должна вывести, что D останавливается, но если D останавливается, то S долж...

Мы получили парадокс, а значит, какое-то из наших предположений неверно. Если программа S существует, то программу D сделать очень просто. Значит, ошибочное предположение было в том, что существует программа S, которая решает проблему остановки.

Следовательно, проблема остановки неразрешима.

А причем здесь большие числа?

(ща все будет, не боись)

Возьмем все машины Тьюринга с произвольными правилами, числом состояний головки N и числом возможных символов M. Запустим их все на ленте, заполненной каким-то одним символом, и "посмотрим", какие из этих машин останавливаются, а какие нет. Из тех, что останавливаются, возьмем ту, которая останавливается за наибольшее число шагов. Обзовем эту машину Busy Beaver (рус. занятой бобр). (Аналогию с занятыми бобрами я считаю еще более запутывающей, поэтому объяснять ее не буду). Определим функцию BB(N, M), которая возвращает, собственно, число шагов до остановки машины Busy Beaver при числе состояний N и числе символов M. Эта функция, очевидно, невычислима, так как, чтобы ее вычислить, нужно решить проблему остановки. Более того, эта функция растет быстрее любой вычислимой функции!

Доказательство:

Пусть существует вычислимая функция f(N, M), которая растет так же или быстрее, чем BB(N, M). Но функцию f(N, M) можно записать в виде программы, а значит, и в виде машины Тьюринга для числа N_0 состояний и M_0 символов.

Возьмем теперь машину Тьюринга с N_1 > N_0 состояниями и M_1 > M_0 символами. Если эта машина не остановилась за f(N_1, M_1) шагов, то она уже не остановится, ведь мы предположили, что f(N_1, M_1) — это оценка сверху числа BB(N_1, M_1).

Но это значит, что, вычислив функцию f(N_1, M_1), мы, по сути, решим проблему остановки для любой машины Тьюринга с N_1 состояниями и M_1 символами. Следовательно, функция f(N, M) невычислима, и BB(N, M) растет быстрее любой вычислимой функции.

Вообще, что собственно этот ваш BB означает? Если говорить популярно и упрощенно, то BB(N, M) означает самое большое число, которое можно рассчитать с помощью программы, код которой "весит" не больше определенного количества байт. Помните парадокс Берри, с которого мы начинали — это тоже самое, только мы избавились от парадокса.

Как ни странно, BB(N, M) можно вычислить для небольших чисел, когда действительно можно понять, зацикливается программа или нет.

Часто используют другую функцию S(N) = BB(N, 2) — то есть используют машины Тьюринга с двумя символами на ленте, скажем "0" и "1". По состоянию на 2022 год известно, что

1. S(1) = 1

2. S(2) = 6

3. S(3) = 21

4. S(4) = 107. Что-то пока ничего необычного...

5. S(5) больше или равно 47 176 870. Некоторые машины с пятью состояниями демонстрируют слишком сложное поведение для человеческого понимания, поэтому оценка неточная.

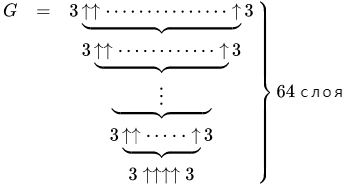
6. S(6) больше или равно вот этому монстру:

, что больше, чем 10↑↑15 (вспомните нотацию Кнута).

Про S(7) нам неизвестно ничего, кроме того, что оно больше S(6).

Умельцы сконструировали машину Тьюринга с 19 состояниями и 2 символами, которая останавливается больше, чем за число Грэма шагов. Скорее всего, S(19) гораздо больше числа Грэма.

Другие мастера доказали, что S(748) невозможно вычислить в системе аксиом Цермело-Френкеля. Скорее всего, настоящая граница гораздо меньше 748.

Вообще (это уже мое предположение), числами S(N) можно измерять "силу" математических теорий: чем "сильнее" теория, тем для большего N можно вычислить S(N). Чтобы вычислить любое S(N), нужна, как мне кажется, бесконечно сложная теория бесконечной силы.

Число Райо из той же оперы, только использует не "язык" машин Тьюринга, а язык теории множеств, и определяется, как "наибольшее число, представимое на языке теории множеств с использованием гугола символов или меньше, плюс 1".

Математики, естественно, не стали останавливаться на этом.

Предположим существование оракула — мистической машины с неизвестным устройством, которая может решать проблему остановки обычной машины Тьюринга. Противоречий здесь никаких нет, потому что оракула нельзя "спросить" с помощью обычной машины. Если же мы позволим некой машине "высшего порядка" обращаться к нему, этот оракул больше не сможет решить проблему остановки по тем же причинам, что и в случае с обычной машиной. Чтобы решить проблему остановки снова, предположим существование "высшего оракула" или "оракула второго порядка". Но и он не сможет решить проблему остановки для машин, которые к нему обращаются. Так же мы можем предположить существование оракулов энного порядка, ну и в конце концов "абсолютного оракула", который может решить проблему остановки для любого оракула конечного порядка. Но и он сам не сможет решить проблему остановки для машин, которые его вызывают. На самом деле можно образовать целую иерархию оракулов, очень похожую на иерархию быстрорастущих функций.

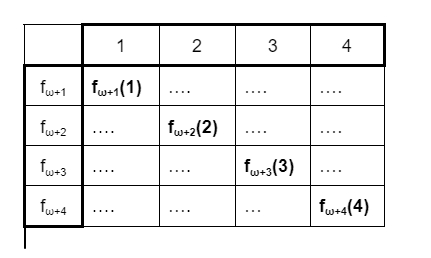
Для машин, использующих оракулы, мы можем определить своих Busy Beavers и свои функции BB_k(N, M), где k — порядок оракула. Каждая следующая функция BB_k(N, M) растет быстрее любой "сверхвычислимой" функции предыдущих порядков.

С помощью похожих конструкций математик Джонатан Бауэрс наконец определил самое большое именованное конечное число в гугологии — Utter Oblivion (рус. Высшее Забвение). Ничего конкретного оно не означает, просто Бауэрс хотел, чтобы его число было самым большим.

Существует ли оракул на самом деле — проблема скорее философская. Есть несколько вариантов для существования оракула в нашем физическом мире, и, как по мне, вряд ли хоть какой-то из них возможен:

1. "Машина Зенона" — может выполнить бесконечное количество шагов за конечное время.

2. "Действительный компьютер" — может вычислить иррациональное число с бесконечной точностью.

3. Квантовый "сверхкомпьютер" с бесконечномерными кубитами (если я правильно понял).

Есть и другие умозрительные конструкции, про них лучше почитайте на Википедии.

Пожалуй, с конечными числами можно на этом закончить, несмотря на то, что даже самое большое из них — ничто по сравнению с бесконечностью. Но о них в следующий раз.

Из этих аксиом можно вывести почти все вам известные факты о натуральных числах. Например:

1. От перемены мест слагаемых сумма не меняется;

2. От перемены мест множителей произведение не меняется;

3. Простых чисел бесконечно много;

4. Между n и 2n обязательно есть простое число;

И множество других теорем, более сложных в доказательстве.

Но некоторые факты нельзя доказать, используя только аксиомы Пеано. И такие факты часто используют функции, растущие также или быстрее, чем

Один из таким фактов — Теорема Гудстейна. (Разбор теоремы на Youtube, 4.5 часа)

Для начала возьмем любое натуральное число и запишем его, как сумму степеней двойки:

Это всегда можно сделать, на этом вообще основана двоичная система счисления. (Вспомните школьный курс информатики).

В числе 2^3 в показателе осталась тройка, и мы можем разложить её также.

Мы получили запись числа 9 в так называемой "наследственной нотации" (англ. "Hereditary base-n notation" по основанию 2.

Теперь механически меняем все двойки в этой записи на тройки и отнимаем в конце единицу.

Переписываем получившиеся число в наследственной нотации по основанию 3. Для этого представляем число в троичной системе счисления, все цифры в этом числе умножаем на соответствующие степени тройки. (Опять же, вспомните системы счисления!). То же повторяем для показателей степеней, пока в итоге не останется чисел, больших 3.

Меняем теперь в этом числе все тройки на четверки и отнимаем в конце единицу. Получившееся число переписываем в наследственной нотации по основанию 4, меняем все 4 на 5 и отнимаем единицу, и так далее, и так далее.

Теорема Гудстейна утверждает, что в конце этой последовательности получится ноль. Кажется абсолютно контринтуитивным, но это так. Последовательность поначалу стремительно растет, но в какой-то момент очередной член последовательности приходит к виду

в наследственной нотации по основанию B, после чего начинает уменьшаться.

Так вот, длина этой последовательности для числа n растет примерно как

что "слишком быстро" для системы аксиом Пеано.

Конечно, математики не ограничиваются системой аксиом Пеано. В системе аксиом Цермело-Френкеля (сейчас неважно, что это за система) теорему Гудстейна доказать можно.

Но ведь быстрорастущая иерархия не заканчивается! Вот примеры, которые я объяснять уже не буду:

И так далее, и тому подобное. Где-то в этом списке есть и еще одно известное число TREE(3), его масштаб строго не доказан, но оценивается, как

И, честно говоря, даже я так глубоко в это не погружался и не отвечу, что все эти греческие буквы означают. Да и это, вообще говоря, уже не имеет значения, так как ничего принципиально нового здесь нет — это всё также рекурсия и диагонализация, погруженные в другие слои рекурсии и диагонализации, погруженные в другие слои ре...

Тем не менее, у математиков нашелся способ строить еще большие числа, но о нём в следующей статье.

На этом графике функция y = x^3 растет быстрее, чем y = x, так как можно выбрать такое x0 (на рисунке оно обозначено), что, начиная с него, значения функции y = x^3 будут всегда больше, чем y = x. Хотя только по графику сказать такого нельзя — вдруг при некотором большом x1 функция y = x обгонит y = x^3? В нашем случае довольно очевидно, что это не так (мы сравниваем число с его кубом).

Теперь к теме.

Быстрорастущая иерархия — это серия функций, в которой каждая следующая растет быстрее предыдущей. Достигается это с помощью двух приемов — рекурсии и диагонализации.

Итак, определим первую функцию в нашей серии как

Эта функция просто прибавляет единицу к числу. Теперь каждую последующую функцию определим, как

То есть мы применяем предыдущую функцию к числу n подряд n раз. Это и есть рекурсия. Например,

Чтобы получить f_1(3), мы применили функцию f_0(n) к числу 3 подряд три раза. Получилось 6. Более того, верна формула

Эта функция уже растет быстрее f_0(n). Попробуем теперь тем же рекурсивным способом вычислить f_2(3).

Применив f_1(x) три раза подряд к числу 3, мы, по сути, удвоили его три раза подряд. Формула здесь такая:

Остановимся и сделаем промежуточные выводы.

Можно заметить, что в f_0(x) мы используем только сложение, в f_1(x) уже появляется умножение, а в f_2(x) — возведение в степень. Вообще говоря, все эти функции являются этаким аналогом гипероператоров (про них мы говорили в предыдущем посте). Напомню: каждый следующий гипероператор растет намного быстрее предыдущего, и уже масштабы тетрации — следующего гипероператора после возведения в степень, — выходят за рамки всего существующего в нашей вселенной.

Примерно оценить масштаб функций f_n(x) можно с помощью нотации Кнута — о ней мы тоже уже говорили:

Здесь знак тильды ("~") означает примерный масштаб. При k = 3 f_k(n) растет уже как тетрация, при k = 4 как пентация, и.т.д.

До сих пор мы не применяли второй прием — диагонализацию. Этот прием позволит нам определить функцию, которая растет быстрее всех тех, что мы уже определили.

Для этого построим вот такую табличку и выделим в ней элементы, стоящие на диагонали:

Если теперь определить функцию, которая выдает значения, стоящие на этой диагонали, то она будет расти быстрее всех, что мы уже определили. На самом деле эта функция, обозначим её как

будет расти быстрее n-ой функции из списка, начиная с числа n+1.

Вот эта греческая буква означает, грубо говоря, "бесконечность", выражая тот факт, что функция f_ω растет быстрее любой функции f_n, где n — любое "конечное" число.

Следующая функция f_[ω+1](n) определяется, как n раз повторенная функция f_ω.

Эта функция уже растет примерно как последовательность g(n) из предудущего поста. Более того,

, где G — число Грэма, то самое.

Например

, где

По сути мы повторили трюк при определении числа Грэма, когда вместо того, чтобы прибавлять стрелочки в нотации Кнута по одной, мы само количество стрелочек задавали теми огромными числами, которые при их использовании получаются.

картинка из второй части

Следующая функция в быстрорастущей иерархии определяется аналогично — повторением предыдущей:

Помните, что число Грэма - это g(64)? Что если взять не g(64), а g( g( 64))? А

? Ничего особенного, мы получим примерный масштаб чисел, которая выдает функция f_[ω+2].

Думаю, вы догадались, что будет дальше. Вот с этим чудовищем можно сравнить f_[ω+3](64):

И так далее, и тому подобное. Но и это еще не конец. Такую же диагонализацию можно применить снова:

И новая "диагональная" функция снова растет быстрее всех предыдущих. Обозначается она, как

Аналогично определяются функции f_[ω2 + 1], f_[ω2 + 2], f_[ω2 + 3], и.т.д, к которым тоже можно применить диагонализацию и получить

Точно так же определяются функции f_ω4, f_ω5, f_ω6, к которым тоже можно применить диагонализацию!

Забудьте про число Грэма. Его мы оставили дааалеко позади.

Чтобы перейти к f_[ω^3], нужно пройти через все предыдщие этапы (знак f опускаю): ω^2 + 1, ω^2 + 2, ω^2 + 3 ... диагонализовать в ω^2 + ω; потом ω^2+ω, ω^2 + ω2, ω^2 + ω3, ^2 + ω4 диагонализовать в ω^2 + ω^2 = (ω^2)*2; и наконец (ω^2)*2, (ω^2)*3, (ω^2)*4 диагонализовать в ω^3. Дальнейшие выкладки по получению ω^4, ω^5 и.т.д. опустим и сразу перейдем к их диагонализации.

Точно также строится последовательность ω^ω, ω^ω^ω, ω^ω^ω^ω и.т.д., которая диагонализуется в

В этом посте слишком много картинок, поэтому здесь будет ссылка на вторую часть о быстрорастущей иерархии.

Здесь число под фигурной скобкой означает количество повторений. Вроде бы понятно.

Соответсвенно, каждый следующий гипероператор определяется как итерированное применение предыдущего. Вот пример для умножения — ведь это повторенное несколько раз сложение!

Стоит заметить, что умножение, как гипероператор 2 порядка, уже действует намного эффективнее. Сравните, например, числа 10 + 20 и 10*20 — разница уже почти на порядок.

Следующий гипероператор — возведение в степень, определяется (как бы вы думали?), через повторенное умножение!

И здесь мы уже улетаем в стратосферу. Вспомните, что числа из первого поста мы определяли именно через степени, а они уже не вмещались в нашу Вселенную!

Но что насчет следующего гипероператора? В школе о нем не говорят, да и в универе вроде не проходят. Дело в том, что тетрация растет настолько быстро, что почти ни в одной из задач, не созданных специально, её нельзя применить!

Записывать тетрацию, как «башню степеней», несколько неудобно, поэтому стоит познакомиться с альтернативной формой записи гипероператоров — стрелочной нотацией Кнута. Возведение в степень в этой форме записывается вот так:

А тетрация — вот так:

Стоит заметить, что на этом этапе математика уже начинает потихоньку ломаться, и результат тетрации будет зависеть от того, как расставить скобки. Например:

Как видно в примере, если вычислять выражение сверху вниз, результат получится больше. Математики делают именно так.

Чтобы понять масштаб чисел, попробуем что-нибудь посчитать:

В этом числе уже содержится 65536 цифр!
Ну а в числе 2↑↑6 количество цифр будет равно 2↑↑5.

В числе 2↑↑7 количество цифр будет равно 2↑↑6, и.т.д.

(Примечание: Количество цифр в двоичной записи. В десятичной записи цифр будет примерно в 3 раза меньше, что не имеет особого значения на таких масштабах).

Уже 2↑↑6 нельзя записать в обычном десятичном виде, даже если мы бы могли записать цифру в каждом атоме вещества во вселенной. Даже если бы в каждом атоме во Вселенной содержалась целая мини-вселенная, мы бы не смогли записать и толику цифр этого числа на всех атомах мини-вселенной в каждом атоме нашей вселенной. Чтобы все-таки это сделать, уровень вложенности этих мини-вселенных должен быть равен примерно 250. Хотя, признаюсь честно, мог ошибиться. Разбор в комментариях приветсвую)

Повторюсь — это все про число 2↑↑6, а уже в числе 2↑↑7 количество цифр равно 2↑↑6, и.т.д.

(Картинка для стимуляции воображения™ )

А ведь это только тетрация — четвертый по счету гипероператор.

Пентация, гексация, и последующие гипероператоры в нотации Кнута записываются аналогично предыдущим — количество стрелок на 2 меньше порядка гипероператора.

Вот пентация:

И гексация:

Не забываем, что вычислять нужно справа налево!

Слишком много стрелочек писать долго, поэтому n-тацию сократим следующим образом:

Хоть как-то осознать масштаб пентации еще можно, так что приведу пример.

Вспомните тетрацию: количество цифр в числе 3↑↑7625597484987 равно числу 3↑↑(7625597484987 - 1). Дальше думайте сами, а я себя лучше пожалею.

Теперь мы готовы, чтобы поговорить о числе Грэма.

В свое время его записали в книгу рекордов Гиннесса, как «самое большое число, когда-либо участвовавшее в серьезном математическом доказательстве». Сейчас это уже не так, но об этом в следующей части.

Число Грэма — оценка числа измерений пространства (обозначим, как N), при котором начинает выполняться некоторое комбинаторное свойство N-мерного гиперкуба. Если вы когда-то пытались представить 4 измерения, и вас не получилось — даже не пытайтесь представить пространство с числом Грэма измерений. Не получится.

(воображение уже не поможет, задействуйте абстрактное мышление™)

Не получится и определить его напрямую через нотацию Кнута, но можно итеративно. (Вспомните, как мы в начале поста определили сложение). Поехали.

Первое число в последовательности — g(1), определим как

Уже g(1) находится вне досягаемости в принципе чего угодно. Следующее — g(2), уже нельзя определить через нотацию Кнута напрямую, ведь количество стрелочек уже равно g(1).

В числе g(3) уже g(2) стрелочек, в g(4) — g(3) стрелочек, и.т.д. Число Грэма — это 64 число в последовательности, то есть g(64).

(картинка из википедии)

Не имеет смысла писать, насколько это много.

Поэтому скажу только, что в терминах быстрорастущей иерархии последовательность g(n) примерно порядка

и это только самое начало. Но об этом в следующий раз. Ждите через пару недель.