Парадокс закона Архимеда
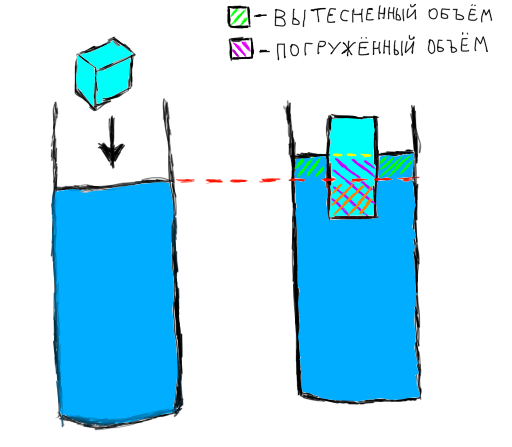
Существуют две разные формулировки закона Архимеда: "выталкивающая сила равна весу жидкости в объёме погружённой части тела" и "выталкивающая сила равна весу вытесненной телом жидкости". На первый взгляд кажется, что эти формулировки эквивалентны, ведь объём вытесненной жидкости равен погружённому объёму. Но на самом деле это абсолютно неверно. Чтобы понять почему, взглянем на рисунок.
В стакан с водой мы опускаем кубик льда. Красной пунктирной линией обозначен старый уровень воды, жёлтой — новый. Зелёным заштрихован вытесненный объём, фиолетовым — погружённый, а оранжевым — тот объём льда, который погружён ниже красной линии. Поскольку вода несжимаема, ясно, что зелёный объём равен оранжевому. Но как видно из рисунка, оранжевый объём является частью фиолетового. Фиолетовый объём намного больше оранжевого. А поскольку оранжевый равен зелёному, фиолетовый больше зелёного. Это означает, что погружённый объём больше вытесненного.
Нетрудно понять, что объём погружённой части всегда будет больше или равен вытесненному. Ведь вытесненный объём равен тому объёму тела, который погружён ниже старого уровня жидкости, а он, в свою очередь, является частью общего погружённого объёма. Значит, вытесненный объём будет равен погружённому только в том случае, когда вся погружённая часть тела находится ниже старого уровня жидкости.
Но если погружённый и вытесненный объёмы не равны, возникает вопрос: какая же формулировка закона Архимеда верна? Чтобы ответить на него, вспомним, как выводится закон Архимеда.
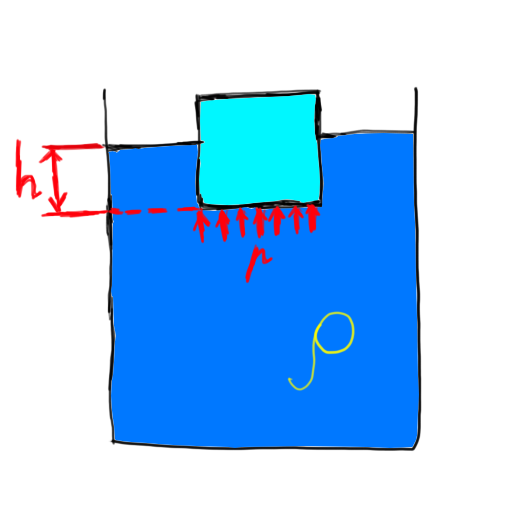
Вернёмся ко льду в воде. Пусть он погружён на глубину h. В любой точке на этой глубине давление равно ρgh, где ρ — плотность жидкости, g — ускорение свободного падения, h — глубина. По закону Паскаля давление передаётся без изменений во всех направлениях. Таким образом, это давление жидкость оказывает на нижнюю грань кубика. Пусть её площадь равна S. Тогда сила давления на нижнюю грань кубика равна ρghS = ρgV, где V — объём погружённой части кубика (V = hS). Эта сила и есть выталкивающая. Таким образом, получается, что выталкивающая сила равна весу жидкости в объёме погружённой части тела, а вовсе не весу вытесненной жидкости.
Из всего вышесказанного также следует, что водоизмещение корабля совсем не обязательно будет равно его массе (если под водоизмещением мы подразумеваем массу вытесненной воды). Поскольку корабль не тонет, сила тяжести, действующая на него, равна силе архимеда:
mg = ρgV (m — масса корабля, g — ускорение свободного падения, ρ — плотность воды, V — погружённый объём).
Разделив это уравнение на g, получим
m = ρV.
Обозначим объём вытесненной воды как Vвыт. Поскольку
Vвыт ≤ V,
то
ρVвыт ≤ ρV ⇔ ρVвыт ≤ m.
Но ρVвыт — это масса вытесненной воды, то есть, водоизмещение. Следовательно, водоизмещение меньше или равно массе корабля.
Ситуацию, когда водоизмещение меньше массы корабля, проще всего наблюдать, когда корабль плавает в тесном доке. Даже если масса воды в доке меньше массы корабля, он всё равно не будет касаться дна, несмотря на то, что не будет вытеснять воду с массой, равной своей.