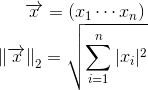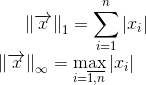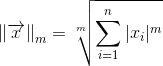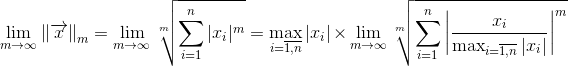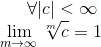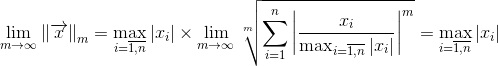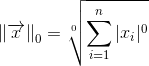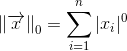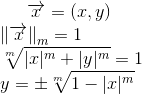Немного о нормах
Всем привет. В самый разгар новогодних каникул хотелось бы рассказать немного о нормах.
Различные нормы широко используются в самых разных разделах математики. Всем со школы знакома Евклидова норма:
Довольно часто используется первая и бесконечная нормы:
Сегодня я попытаюсь рассказать, почему они так нумеруются.
В общем виде норма счётномерного вектора определяется следующим образом:
При m = 1 получаем первую норму (сумму модулей компонент). При m = 2 получаем вторую норму (Евклидову).
При необходимости можно рассмотреть случай с 0 < m < 1.
Рассмотрим предельные случаи.
Первый случай: бесконечная норма. m -> inf.
Здесь все члены суммы меньше или равны единице. Так как:
То:
Что и приводит нас к бесконечной норме.
Второй случай называют также часто нормой Хэмминга. Он реализуется при m = 0. Формально запишем определение нормы:
Нам создаёт проблемы корень нулевой степени (означающий, фактически, возведение в пределе в бесконечную степень). Для сведения нулевой нормы к норме Хэмминга выкинем этот корень:
Учитывая, что 0^0=0, получаем норму Хэмминга.
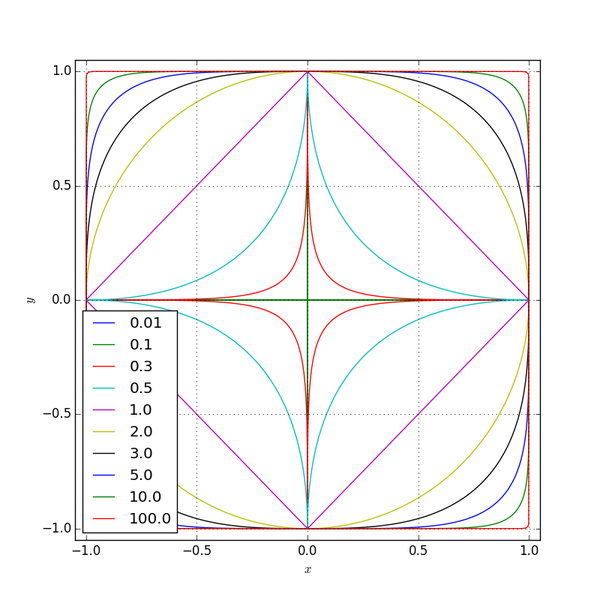
Может быть крайне интересно посмотреть на вид единичных окружностей в разных нормах. Решая аналитически следующее уравнение:
можно построить графики соответствующих окружностей:
В случае первой нормы окружность является ромбом. В случае второй (Евклидовой) нормы окружность имеет привычный нам вид. При увеличении m она всё больше и больше переходит в квадрат (окружность бесконечной нормы). При уменьшении m окружность стремится к кресту, характерному для нулевой нормы.
Благодарности:
Формулы были написаны при помощи онлайн редактора LaTeX.
График был построен с использованием библиотеки модулей matplotlib для языка Python.
Решение уравнения было выполнено с использованием языка C в среде Code::Blocks, работавшей в операционной системе Windows 7.
Длиннопост был выполнен с использованием встроенного редактора на сайте pikabu.ru.