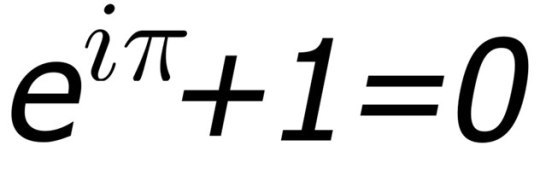Математические факты, в которые сложно поверить. Часть 1.⁠⁠

1. Про дни рождения

Если у нас в классе 23 человека то существует 50% шанс того, что среди них как минимум двое родились в один день. Если же вы соберёте 70 человек, то вероятность этого будет равна 99.9%.

Как же так? В году 365 дней и каждый из одноклассников мог родиться в любой из них. Но стоит понять, что мы тут не сравниваем одного ученика со всеми, для поиска пары мы сравниваем всех со всеми, т.е. число испытаний у нас значительно больше 23-х. Подробно этот "парадокс" разбирается в википедии: https://ru.wikipedia.org/wiki/Парадокс_дней_рождения

2. Колода карт

Вы когда-нибудь задумывались, как много комбинаций получается при перемешивании колоды карт? А что если я скажу, что если вы сейчас тщательно перемешаете карты, то создадите комбинацию, которая за всю историю человечества никому и никогда не выпадала? Те, кто в школе/универе не пропускал комбинаторику, знают что число этих комбинаций равно 52! (если речь про колоду с 52-я картами). Но насколько велико это число? Как с расстояниями в космосе наш мозг не способен осознать такие величины. В комментариях приводилось несколько попыток описать эти масштабы, но мне больше всего понравилось следующее:

«Если бы у каждой звезды в нашей галактике было бы триллион планет с триллионом людей на каждой из них. И у каждого человека было бы триллион колод карт, каждую из которых он бы как-то умудрился перемешивать со скоростью 1000 раз в секунду. И вся эта движуха началась бы с момента большого взрыва, то только к настоящему моменту стали бы появляться комбинации, которые уже встречались».

Из той же серии байка про зерна и шахматную доску и предложение сложить несколько раз лист бумаги (при 103 сгибе его толщина превысит внезапно размеры вселенной)

3. Тождество Эйлера

А теперь давайте поймём почему математики всего мира бьются в конвульсиях и оргазмируют при виде этого тождества. Все очень просто - здесь собраны ключевые математические константы и математические операции. При этом, что больше всего поражает - показана связь между мнимой единицей (квадратный корень из -1) и вещественным числами. По-большому счету условность, принятая математиками, оказалась вполне осязаемой величиной.

4. Парадокс маляра

Тут уже позабористей штука. В русскоязычной литературе парадокс называется "парадоксом маляра". Он гласит то, что фигуру с бесконечной площадью поверхности можно окрасить конечным числом краски. В англоязычной литературе это уже горн Гавриила (что и нарисовано на каритнке). Все подобные парадоксы объясняются сходящимися рядами. Когда у нас есть бесконечная последовательность, которая в сумме даёт конечно число, e.g.: 2 = 1 + 1/2 + 1/4 + 1/8 ... Или другими словами слой краски будет с каждым разом всё тоньше и тоньше, вот и вся загадка.

5. Захомутать Землю

Если обернуть верёвкой Землю по экватору - сколько потребуется добавить верёвки, что бы поднять верёвку на один метр над поверхностью всей Земли? 10 000 км? 1 км? Ответ: 6.3 метра. В виду того, что Земля такая большая интуиция нас обманывает. Нам кажется, что увеличение радиуса сильно зависит от длины окружности, но это не так. Стоит описать задачу через формулы - всё становится очевидным, в википедии даже отдельная статья есть с доказательством: https://en.wikipedia.org/wiki/String_girdling_Earth.

Наверняка найдутся люди, которым все эти факты покажутся очевидными. Рад за вас, значит вы обладаете хорошей математической интуицией. :) На этом закончим первую часть. Если зайдёт, продолжим дальше с менее баянистыми фактами.