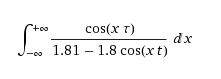Просьба к лиге математиков
Может есть на Пикабу люди способные решить данный интеграл? Мозги уже кипят. Коммент для минусов внутри
раскрыть ветку (10)
раскрыть ветку (3)
раскрыть ветку (2)
неужели вот эти 0.9944 делают погоду? нельзя округлить до единицы? тогда домножаешь на (1+cos(xt)) и сводишь к квадрату синуса. я уже конечно года два такое не решал, но стало интересно
если ты делаешь замену, то нужно заменять и предел интегрирования, а предел интегрирования синуса и косинуса на бесконечности неопределён. если я не ошибаюсь.
раскрыть ветку (5)
Ошибаешься, нельзя интегрировать cos(Tx) по cos(tx), есть у меня такое чувство что автор где-то налажал и t выражается через T, т.к. задача явно не по матану судя по изначальной формулировке, так же, судя по тому, что я не нашел похожего у Градштейна-Рыжика, то я склоняюсь к тому, чтобы брать его численно, разложением в ряд.
раскрыть ветку (4)
Они не выражаются. Задача по Статистической радиотехнике. В справочнике я тоже ничего не нашел, именно поэтому Пикабу последняя надежда)
раскрыть ветку (2)
Если делать замену получишь следующее еще не дойдя до косинуса:
cos(Tx)/(1.81 - 1.8cos(tx)) dx = 1/t cos(Tx)/(1.81 - 1.8cos(tx)) d(tx) - это поплава
Работало бы, если:
cos(tx)/(1.81 - 1.8cos(tx)) dx = 1/t cos(tx)/(1.81 - 1.8cos(tx)) d(tx) = ... - ну и дальше по списку.
раскрыть ветку (1)
А, вот вы о чём. Возможно там на самом деле одинаковые "т" в скобках или иначе я вообще хз как это решать)