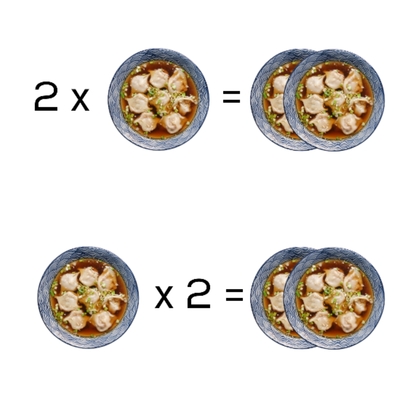Я бы сказал, что требуя именно такого порядка вычисления, а не произвольного, учитель хочет сфокусировать внимание на понимании размерностей, что в дальнейшем КРАЙНЕ важно. Двойку ставить действительно слишком, ответы численно верные - но вот как минимум убедиться в понимании учеником идеи надо. А то будут потом метры на градусы делить - а ответ получать в человеках.
раскрыть ветку (1)
Нам в начальной школе говорили только про то, что от перемены множителей произведение не меняется. И я считаю логично детям не забивать голову тем, что им понадобится ещё очень не скоро. Можно упомянуть, что в старших классах будут задачи/уравнения, для которых важно где что находится, но не сейчас. Потому что конкретно для таких задач разницы действительно нет
показать ответы
Это задачи, а не примеры, не надо путать. В комментарии всё правильно сказано. А вот двойка за работу, конечно жёстко.
раскрыть ветку (1)
Ну, допустим, она права. Тогда в чем принципиальная разница в решении, если ответ будет один и тот же?
Возьмём одну тарелку с 8-ю пельменями. Сколько пельменей будет в 2-х тарелках? Очевидно, что 16. Так какая разница, где стоит множитель, а где тарелка с пельменями в решении задачи, если по итогу у нас будет 16 пельменей на две тарелки?
показать ответы
Так-то понимание логики действий важнее арифметики. А просто угадать правильный ответ - не имеет смысла.
раскрыть ветку (1)
ну двойку за это ставить конечно глупо, но вообще объяснение дельное, оно про логику, а не про математику
раскрыть ветку (1)
а можно просто сварить пельмени, положить по восемь в разные тарелки, потом ссыпать в одну и загибая пальцы пересчитать, ответ тоже будет верный
раскрыть ветку (1)
раскрыть ветку (1)
Вы всё ещё уходите от прямого ответа. Я и считал количество пельменей(!) в двух тарелках. А не сами тарелки. Тарелки тут особой роли не играют, я просто не нашел фотки пельменей без посуды
показать ответы