Айсберг больших чисел. Часть 3.1. Дно айсберга
В предыдущих частях мы поговорили о некоторых очень больших числах, объяснение сути которых занимает не более одной страницы и пообещали рассказать о быстрорастущей иерархии. Прочитайте сначала их, иначе в этом посте ничего не поймете!
Пару дисклеймеров:
Функции быстрорастущей иерархии не имеют никакого отношения к реальности. Это игра разума некоторых математиков и попытка понять, насколько далеко может зайти абстракция. Числа здесь будут настолько большие, что я даже не буду пытаться подобрать к ним разные "невообразимые" эпитеты.
Этот пост — самый сложный для понимания из серии (хоть впереди еще два). Воображение вам уже не понадобится, зато нужна будет немалая доля абстрактного мышления и математическая интуиция. 7-8 класса школьной математикии всё ещё достаточно. Ну и да, формул будет много.
Значок "^" будет означать степень, звездочка "*" — умножение, а нижнее подчеркивание "_" — нижний индекс.
Прежде чем перейти непосредственно к быстрорастущей иерархии, нам нужно понять, как сравнивать функции между собой.
По (нестрогому) определению, функция g(x) растет быстрее функции f(x), если значения функции g(x) становятся больше значений f(x) начиная с некоторого числа x0. Вот пример:
На этом графике функция y = x^3 растет быстрее, чем y = x, так как можно выбрать такое x0 (на рисунке оно обозначено), что, начиная с него, значения функции y = x^3 будут всегда больше, чем y = x. Хотя только по графику сказать такого нельзя — вдруг при некотором большом x1 функция y = x обгонит y = x^3? В нашем случае довольно очевидно, что это не так (мы сравниваем число с его кубом).
Теперь к теме.
Быстрорастущая иерархия — это серия функций, в которой каждая следующая растет быстрее предыдущей. Достигается это с помощью двух приемов — рекурсии и диагонализации.
Итак, определим первую функцию в нашей серии как
Эта функция просто прибавляет единицу к числу. Теперь каждую последующую функцию определим, как
То есть мы применяем предыдущую функцию к числу n подряд n раз. Это и есть рекурсия. Например,
Чтобы получить f_1(3), мы применили функцию f_0(n) к числу 3 подряд три раза. Получилось 6. Более того, верна формула
Эта функция уже растет быстрее f_0(n). Попробуем теперь тем же рекурсивным способом вычислить f_2(3).
Применив f_1(x) три раза подряд к числу 3, мы, по сути, удвоили его три раза подряд. Формула здесь такая:
Остановимся и сделаем промежуточные выводы.
Можно заметить, что в f_0(x) мы используем только сложение, в f_1(x) уже появляется умножение, а в f_2(x) — возведение в степень. Вообще говоря, все эти функции являются этаким аналогом гипероператоров (про них мы говорили в предыдущем посте). Напомню: каждый следующий гипероператор растет намного быстрее предыдущего, и уже масштабы тетрации — следующего гипероператора после возведения в степень, — выходят за рамки всего существующего в нашей вселенной.
Примерно оценить масштаб функций f_n(x) можно с помощью нотации Кнута — о ней мы тоже уже говорили:
Здесь знак тильды ("~") означает примерный масштаб. При k = 3 f_k(n) растет уже как тетрация, при k = 4 как пентация, и.т.д.
До сих пор мы не применяли второй прием — диагонализацию. Этот прием позволит нам определить функцию, которая растет быстрее всех тех, что мы уже определили.
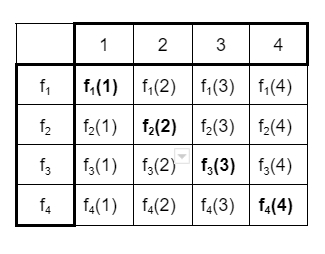
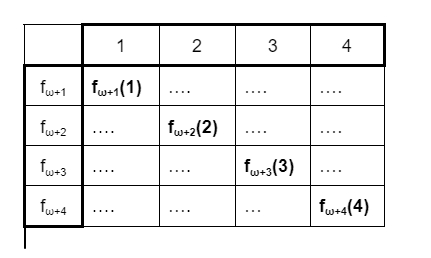
Для этого построим вот такую табличку и выделим в ней элементы, стоящие на диагонали:
Если теперь определить функцию, которая выдает значения, стоящие на этой диагонали, то она будет расти быстрее всех, что мы уже определили. На самом деле эта функция, обозначим её как
будет расти быстрее n-ой функции из списка, начиная с числа n+1.
Вот эта греческая буква означает, грубо говоря, "бесконечность", выражая тот факт, что функция f_ω растет быстрее любой функции f_n, где n — любое "конечное" число.
Следующая функция f_[ω+1](n) определяется, как n раз повторенная функция f_ω.
Эта функция уже растет примерно как последовательность g(n) из предудущего поста. Более того,
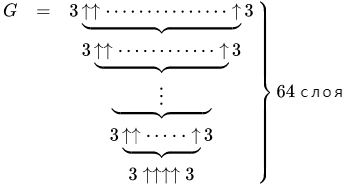
, где G — число Грэма, то самое.
Например
, где
По сути мы повторили трюк при определении числа Грэма, когда вместо того, чтобы прибавлять стрелочки в нотации Кнута по одной, мы само количество стрелочек задавали теми огромными числами, которые при их использовании получаются.
картинка из второй части
Следующая функция в быстрорастущей иерархии определяется аналогично — повторением предыдущей:
Помните, что число Грэма - это g(64)? Что если взять не g(64), а g( g( 64))? А
? Ничего особенного, мы получим примерный масштаб чисел, которая выдает функция f_[ω+2].
Думаю, вы догадались, что будет дальше. Вот с этим чудовищем можно сравнить f_[ω+3](64):
И так далее, и тому подобное. Но и это еще не конец. Такую же диагонализацию можно применить снова:
И новая "диагональная" функция снова растет быстрее всех предыдущих. Обозначается она, как
Аналогично определяются функции f_[ω2 + 1], f_[ω2 + 2], f_[ω2 + 3], и.т.д, к которым тоже можно применить диагонализацию и получить
Точно так же определяются функции f_ω4, f_ω5, f_ω6, к которым тоже можно применить диагонализацию!
Забудьте про число Грэма. Его мы оставили дааалеко позади.
Чтобы перейти к f_[ω^3], нужно пройти через все предыдщие этапы (знак f опускаю): ω^2 + 1, ω^2 + 2, ω^2 + 3 ... диагонализовать в ω^2 + ω; потом ω^2+ω, ω^2 + ω2, ω^2 + ω3, ^2 + ω4 диагонализовать в ω^2 + ω^2 = (ω^2)*2; и наконец (ω^2)*2, (ω^2)*3, (ω^2)*4 диагонализовать в ω^3. Дальнейшие выкладки по получению ω^4, ω^5 и.т.д. опустим и сразу перейдем к их диагонализации.
Точно также строится последовательность ω^ω, ω^ω^ω, ω^ω^ω^ω и.т.д., которая диагонализуется в
В этом посте слишком много картинок, поэтому здесь будет ссылка на вторую часть о быстрорастущей иерархии.



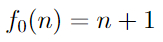
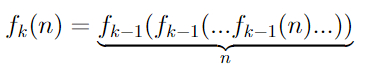


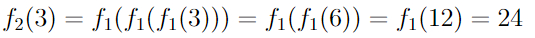
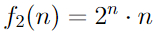
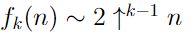
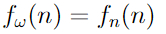
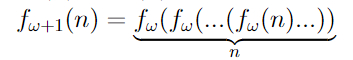
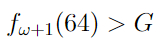
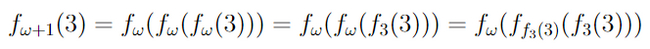
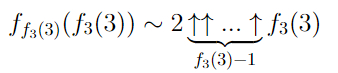

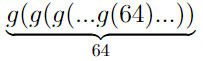
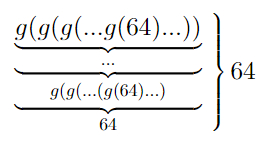
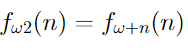
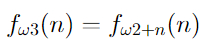
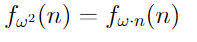
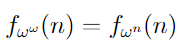
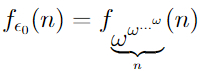
Наука | Научпоп
9.4K постов83K подписчиков
Правила сообщества
Основные условия публикации
- Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
- Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
- Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
- Видеоматериалы должны иметь описание.
- Названия должны отражать суть исследования.
- Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
- Посты-ответы также должны самостоятельно (без привязки к оригинальному посту) удовлетворять всем вышеперечисленным условиям.
Не принимаются к публикации
- Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
- Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
- Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
Наказывается баном
- Оскорбления, выраженные лично пользователю или категории пользователей.
- Попытки использовать сообщество для рекламы.
- Фальсификация фактов.
- Многократные попытки публикации материалов, не удовлетворяющих правилам.
- Троллинг, флейм.
- Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает и общество Пикабу.