Числа Люка
Данный пост не о хайповом не так давно люке в лесу, не о Люке Скайуокере и даже не о Люке Скайуокере в лесу.
Данный пост о последовательности чисел, которые называются "Числа Люка", и о их связи с так называемым Золотым сечением.
Многие наверняка уже слышали о числах Фибоначчи и их связи с Золотым сечением (если нет, это легко гуглится, или вот неплохая статья: тык).
Числа Фибоначчи, как известно, выглядят следующим образом:
Эдуард Люк подумал: а что если начать последовательность не с 1 и 1, а с 1 и 2. Однако если так сделать, то получится та же самая последовательность, но только без первой единицы. Тогда он решил поменять местами числа и начать последовательность не с 1 и 2, а с 2 и 1. Остальное все также: следующее число равно сумме двух предыдущих.
Таким образом последовательность чисел Люка выглядит так:
А теперь про связь с Золотым сечением.
Как известно, Золотое сечение Ф = 1.618033988749...
Всё, что мы будем делать, это возводить это число Ф в степень и округлять до ближайшего целого. И вот, что из этого получится:
Округленные числа совпадают с числами Люка. Таким образом мы из числа Ф получили последовательность чисел Люка. И у данных чисел связь с Золотым сечением выглядит даже сильнее, чем у тех же хайповых известных числах Фибоначчи.
Кто-то может сказать: "Всё это, конечно, здорово, последовательность получается. Но получается она посредством довольно грубого округления". На это можно ответить, что люди связывают математику с порой излишней точностью. Как будто если мы запишем миллион чисел после запятой, это будет только точнее отображать какое-то число. Но данный пример доказывает, что и при округлении можно получать замечательные результаты.


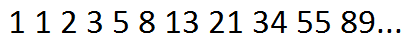
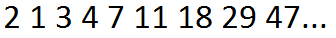
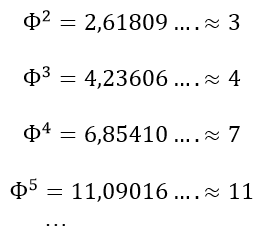
Лига математиков
946 постов2.5K подписчиков