Метод критического пути (Critical Path Method, CPM) является одной из ключевых технологий управления проектами второй половины XX века, оказавшей фундаментальное влияние на развитие современной дисциплины проектного управления. Его появление не было случайностью: метод стал прямым ответом на усложнение индустриальных процессов, рост масштабов инженерных и строительных проектов, необходимость минимизации затрат и повышения эффективности. В отличие от более ранних инструментов, таких как диаграммы Ганта, метод CPM позволил перейти от статического планирования к динамическому анализу взаимосвязей между задачами, выявлению наиболее уязвимых мест проекта и оптимизации его графика.
Исторические предпосылки возникновения CPM уходят в середину XX века. В этот период мировая экономика находилась на подъёме: восстановление после Второй мировой войны требовало строительства заводов, электростанций, транспортной инфраструктуры, жилья. Параллельно развивалась химическая и нефтехимическая промышленность, где каждая остановка технологической линии означала колоссальные убытки. Руководители компаний всё яснее осознавали, что традиционные подходы к планированию, основанные на интуиции и опыте отдельных специалистов, перестают справляться с возрастающей сложностью проектов. Одновременно развивалась вычислительная техника: компьютеры начали использоваться для инженерных расчётов, что создавало предпосылки для автоматизации планирования.
В этих условиях компании DuPont и Remington Rand в 1956–1957 годах разработали метод критического пути. Первоначальной целью было сокращение сроков ремонтов химических заводов, которые обходились компании в миллионы долларов. Каждый простой оборудования приводил к потерям, и руководство искало способ предсказать, какие именно операции являются наиболее «узкими местами» в графике ремонтных работ. Так родилась идея построения сетевого графика, где все задачи проекта представлены в виде узлов и связей, а вычисление длительности определённых последовательностей позволило выявить критический путь — то есть ту цепочку работ, которая определяет минимальную продолжительность всего проекта.
Сетевой график изображается в виде схемы:
вершины (узлы) — события (начало или окончание задач),
дуги (стрелки) — работы, которые необходимо выполнить.
Сетевой график впервые дал управленцам возможность формально рассчитывать сроки завершения проекта, прогнозировать его продолжительность и определять, какие задачи требуют особого внимания.
Пример проекта: подготовка научной конференции
Чтобы показать, как работает метод критического пути, рассмотрим небольшой проект — подготовку и проведение научной конференции.
Определяем задачи
Первый шаг состоит в том, чтобы зафиксировать список всех действий, необходимых для выполнения проекта.
В нашем проекте действия выглядят следующим образом:
A: Определение темы и программы
B: Приглашение спикеров
C: Поиск и аренда помещения
D: Подготовка рекламных материалов
E: Регистрация участников
F: Подготовка оборудования
G: Проведение конференции
Устанавливаем зависимости
B и D зависят от A (нужно сначала определить тему).
E зависит от завершения B и D.
F зависит от C (площадка нужна для настройки техники).
G зависит от E и F.
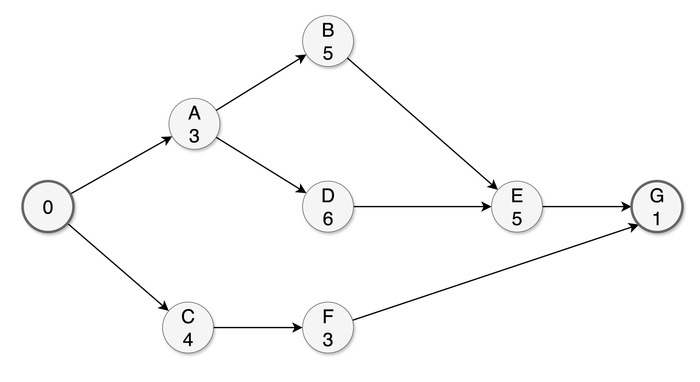
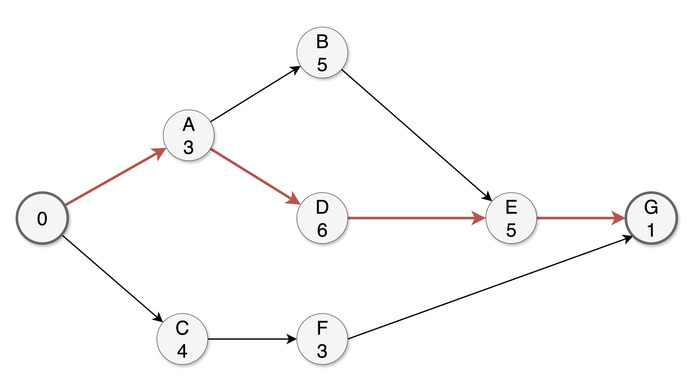
Таким образом, сетевой график проекта имеет вид:
Оцениваем их продолжительность
Для оценки продолжительности задач применяются разные методы:
Экспертная оценка — специалисты, участвующие в проекте, дают прогнозы на основе своего опыта.
Аналогия — используется информация о похожих проектах в прошлом, что позволяет сделать более реалистичные выводы.
Параметрическая оценка — длительность рассчитывается через количественные зависимости (например, «на подготовку одного слайда уходит 30 минут, всего 20 слайдов → 10 часов»).
В нашем проекте оценки выглядят так:
A: Определение темы и программы (3 дня)
B: Приглашение спикеров (5 дней)
C: Аренда помещения (4 дня)
D: Подготовка рекламных материалов (6 дней)
E: Регистрация участников (5 дней)
F: Подготовка оборудования (3 дня)
G: Проведение конференции (1 день)
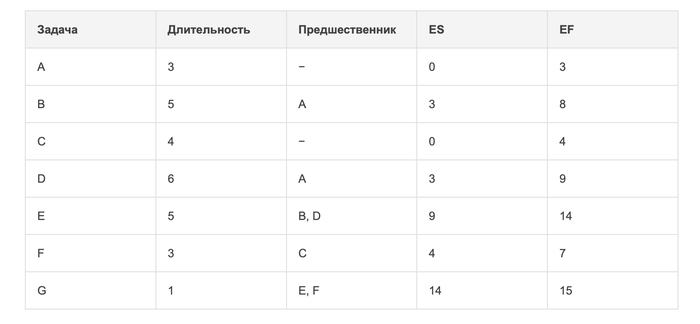
Выполняем прямой ход
Метод прямого хода (forward pass) используется для того, чтобы определить самые ранние возможные сроки начала и окончания задач. Мы начинаем с «нуля» и двигаемся слева направо по сетевой диаграмме. Для каждой работы считаем:
При этом, если у какого-либо действие 2 и более предшественника, то начинать его мы можем только после завершения самого длительного из них. Таким образом мы узнаём, как быстро можно завершить проект, если всё будет идти без задержек.
A: 0–3
B: 3–8
C: 0–4
D: 3–9
E: 9–14 (после B и D)
F: 4–7 (после C)
G: 14–15 (после E и F)
Минимальная длительность проекта составляет 15 дней.
Выполняем обратный ход
Метод обратного хода (backward pass) применяется для того, чтобы определить самые поздние допустимые сроки начала и окончания задач, при которых проект всё равно завершится вовремя. Мы двигаемся справа налево, начиная с даты окончания проекта. Для каждой задачи считаем:
Эти расчёты позволяют понять, у каких задач есть «резерв времени» (float), а какие критически важны и не могут задерживаться.
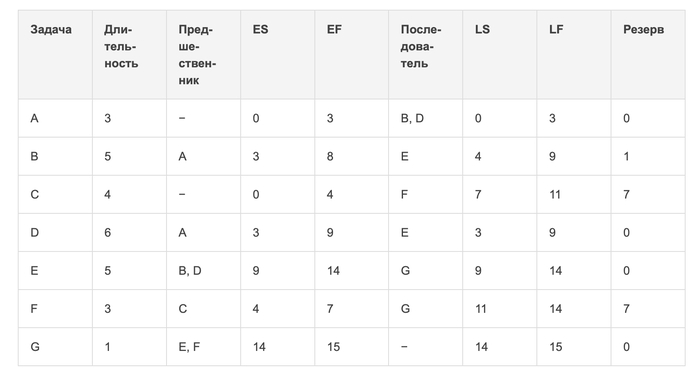
Применим метод, дополнив таблицу прямого прохода. Резерв времени считается по формуле Резерв = LS − ES = LF − EF
Определяем резервы и критический путь
Обратный ход показывает, что задачи A, D, E и G не имеют резерва времени и образуют критический путь. Эти задачи нельзя задерживать: любая просрочка приведёт к срыву конференции. Задача B имеет небольшой резерв в 1 день, а задачи C и F обладают значительным запасом в 7 дней.
Итоговая схема критического пути имеет вид:
Требуемые управленческие решения: держать под особым контролем A, D, E, G; при необходимости перераспределять ресурсы с задач C и F (крупные резервы) и частично с B (малый резерв).
Практика показывает, что одного знания методологии недостаточно: критический путь, диаграммы и сетевые модели остаются лишь схемами на бумаге, если их не встроить в реальные процессы компании. На практике возникает множество нюансов — от распределения ресурсов и приоритизации задач до регулярного пересмотра планов при изменении внешних условий. Именно здесь проявляется ценность профессионального внедрения проектного управления: специалисты помогают адаптировать методы, такие как CPM, под конкретную организацию, учесть особенности её команды и культуры, наладить регулярные управленческие циклы. Такой подход позволяет превратить теорию в рабочий инструмент, который действительно сокращает сроки, снижает риски и обеспечивает предсказуемость проектов. Именно такие задачи мы решаем, сопровождая компании при внедрении систем проектного управления.
Недостатки метода CPM
Несмотря на очевидные достоинства и широкую применимость, метод критического пути имеет и ряд существенных ограничений. Одним из них является жёсткость модели. CPM предполагает, что все задачи имеют фиксированные длительности и зависимости. На практике же многие проекты подвержены изменениям: поставки задерживаются, заказчик вносит новые требования, ресурсы становятся недоступными. В таких условиях график быстро устаревает, и поддерживать его актуальность становится затруднительно.
Другой проблемой является сложность использования CPM для очень больших проектов. Когда сеть насчитывает тысячи операций, диаграммы становятся чрезмерно громоздкими и трудными для восприятия. Хотя современные программы позволяют рассчитывать критический путь автоматически, интерпретация полученной модели всё равно требует значительных усилий.
Следует отметить и то, что классический CPM не учитывает ресурсов. Метод показывает только длительности и взаимосвязи задач, но не отвечает на вопрос, достаточно ли у организации рабочей силы, оборудования или материалов для параллельного выполнения запланированных операций. В реальной жизни это может привести (и обязательно приводит!) к нереалистичным планам, где несколько критических задач требуют одного и того же ресурса одновременно.
Метод также зависит от точности исходных данных. Если оценки длительности задач сделаны неверно, то и расчёт критического пути теряет практическую ценность. В отличие от метода PERT, который оперирует вероятностными оценками и учитывает оптимистичные и пессимистичные сценарии, CPM работает только с одним фиксированным числом. Это снижает его применимость в условиях высокой неопределённости.
Элияху Голдратт, автор Теории ограничений (ТОС), в своих работах неоднократно указывал на фундаментальные слабости метода критического пути. По его мнению, CPM опирается на нереалистичное допущение о фиксированности сроков выполнения задач, игнорируя поведение исполнителей и особенности организационной среды. Голдратт отмечал, что при составлении графика каждая задача получает избыточный «запас времени» на случай непредвиденных задержек. Однако этот запас не только не страхует проект, но зачастую приводит к так называемому «синдрому студента» (откладывание работы до последнего момента) и эффекту Паркинсона (растягивание работы на всё отпущенное время). В результате фактическая длительность операций становится больше, чем могла бы быть, а общий график проекта сдвигается.
Кроме того, Голдратт подчеркивал, что метод CPM не учитывает конкуренцию за ресурсы. Даже при корректно рассчитанном критическом пути реальные проекты сталкиваются с тем, что один и тот же специалист или оборудование требуются для нескольких задач одновременно. Классическая CPM-модель этого не отражает, что делает расписание «идеальным на бумаге», но малопригодным на практике. В ответ на эти недостатки Голдратт предложил альтернативу — метод критической цепи (Critical Chain Project Management, CCPM), в котором внимание смещается с абстрактных зависимостей между задачами на реальные ограничения системы и ресурсы. Ключевая идея CCPM — убрать излишние резервы из отдельных задач, сосредоточив буфер времени на уровне всего проекта, и тем самым минимизировать потери, вызванные человеческим фактором и ресурсными конфликтами.
Практика научной организация труда. Без марафонов желаний и сторис «успешного успеха».
В Telegram-канале — только рабочие инструменты и кейсы из живого бизнеса.