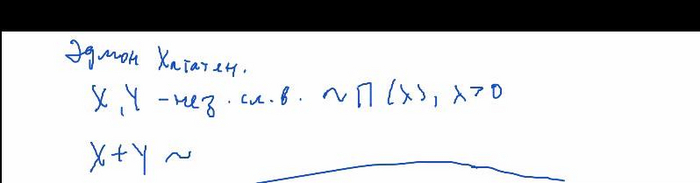Мозг против теории вероятностей
Однажды ко мне после лекции подошла девушка. Она спросила: «А вы точно борец с мракобесием?» А я ей ответил: «Нет, на самом деле я экстрасенс. Загадайте число от 1 до 20». Девушка загадала число, а я ей говорю: «Вы загадали 8!» Моя собеседница очень удивилась: «Вы что, правда экстрасенс? Как вы угадали?» Я сказал, что настоящие ясновидящие не раскрывают секретов. Но с вами я поделюсь своей тайной: всё дело в том, что это была примерно двадцатая девушка, которая подходила ко мне с подобным вопросом после лекции. Правда, числа предыдущих слушательниц мне не удавалось угадать. И вот наконец «чудо» произошло!
Этот пост – про то, как наш мозг нас обманывает. Начну с простой задачки: представьте, что вы кидаете три шестигранных кубика. Вопрос: что вероятнее – что выпавшие числа в сумме составят 3 или 4? Иными словами, что легче получить – три единицы или две единицы и двойку? Несмотря на то, что люди играли с кубиками с незапамятных времён, ответ на такую задачку удалось найти лишь в XIII веке. Итак, вероятность выпадения четвёрки выше. Почему? Дело в том, что сумме, равной четырём, удовлетворяют три «элементарных события»: двойка может выпасть на первом кубике, на втором или на третьем (при условии, что на двух других единицы). А сумму, равную трём, можно получить только одним способом. То есть вероятность выпадения суммы, равной четырём, в три раза выше. Вроде всё просто! Но решение нашлось относительно недавно.
Всё дело в том, что теория вероятностей ужасно контринтуитивна. Люди часто принимают закономерности за случайные события, а случайные события – за закономерности. И сегодня мы разберём, почему это серьёзная проблема – и как она способствует появлению веры в разные странные вещи – в магию, экстрасенсорику, гадания, общение с духом прабабушки и прочие «чудеса».
«Мой мозг предсказал будущее!»
Расскажу историю про человека по имени Рой Салливан. Этот американец работал инспектором по охране национального парка в Вирджинии. Однажды его ударила молния. Потом молния ударила Салливана ещё раз. И ещё. И снова. И опять. Всего, согласно Книге рекордов Гиннесса, молния поражала несчастного рейнджера семь раз – но он остался в живых (в итоге Рой в возрасте 71 года, по версии следствия, покончил с собой из-за неразделённой любви). Кстати, жену Салливана, которая была младше супруга на 30 лет, тоже ударяла молния – и она выжила.
Удар молнии – не самое частое событие. Может показаться, что история Роя – это что-то невероятное и из ряда вон выходящее. Но на самом деле нельзя забывать, что Салливан работал рейнджером в Вирджинии. В этом штате порядка сорока дней в году – штормовые, то есть вероятность попадания в человека молнии в такое время повышается. Кроме того, Салливан работал на природе – ещё одна дополнительная угроза удара молнией. Но это всё мелочи на фоне самого главного. На планете живут миллиарды людей, и подобная история могла произойти с любым из нас. Случись она не с Роем, а с Ромой, мы бы сейчас обсуждали другого человека. Причём не обязательно должна была случиться история с молнией. Может быть, на Рому пять раз напала бы акула или он попал бы в десять автоаварий. Было бы странно, если бы ни с кем никогда не происходили подобные «чудеса».
Вообще чудо – это маловероятное событие, которое иногда с кем-то происходит – и отнюдь не по воле богов или высших сил. Если определить «чудо» как событие, вероятность которого, скажем, 1 к миллиарду в течении одного дня для одного человека, то ежедневно на планете происходит в среднем 8 чудес. Иногда это называют «Законом действительно больших чисел» (не путать с просто «законом больших чисел» из теории вероятностей): на достаточно большой выборке будут случаться крайне маловероятные события. Всё это усугубляется тем, что именно маловероятные события привлекают наш интерес. Например, иногда люди говорят, что им снятся вещие сны. «Мой мозг предсказал будущее, мой сон сбылся!» – рассказывают они. На самом деле сны людям снятся регулярно, но не все они сбываются. Про несбывшиеся сны мы забываем, а вот про один-единственный сбывшийся помним ещё двадцать лет и всем рассказываем. И снова наша жизнь наполняется «чудесами».
Наш мозг обманывает нас и более изощрёнными способами. Вот попробуйте решить ещё одну задачку: где-то на свете живёт девушка Линда. Ей 31 год, она за словом в карман не лезет и очень сообразительна. Она училась на факультете философии. Студенткой много размышляла о дискриминации и социальной несправедливости, участвовала в демонстрациях против распространения ядерного оружия.[ЕШ1]
Вопрос: что более вероятно?
1. Линда – кассир в банке;
2. Линда – кассир в банке и активная феминистка.
Это задачка на «ошибку конъюнкции», которую сформулировали лауреат Нобелевской премии по экономике Даниэль Канеман и психолог Амос Тверски. Правильный ответ на неё – 1, потому что вероятность совместных событий (Линда и кассир, и феминистка) всегда ниже, чем вероятность одного отдельного события (Линда – просто кассир). Канеман и Тверски заметили, что респонденты чаще всего дают на поставленную задачку неправильный ответ. Да и вообще ошибка конъюнкции, которую также называют проблемой Линды, свойственна большинству людей. Но особенно свойственна она тем, кто верит в разные теории заговора и паранормальные явления.
«От гомеопатии никто особо не умирает»
А теперь поговорим о парадоксе Симпсона – явлении в статистике, которое показывает неправомерность обобщений по нерепрезентативным выборкам. Звучит не очень понятно, поэтому объясню на примере: представьте, что вы читаете научную работу об эффективности гомеопатии. Авторы статьи пригласили для исследования 500 добровольцев, страдающих от опасной болезни. 250 из них лечились гомеопатией, вторая половина – нормальными лекарствами с доказанной эффективностью. В итоге выяснилось, что те пациенты, которые лечились сахарными шариками, выздоравливали чаще! Как такое могло произойти с точки зрения теории вероятностей?
Дело в том, что из 500 человек 300 страдали от лёгкой формы болезни, а остальные – от тяжёлой. Из 300 «лёгких» 200 лечились гомеопатией, а 100 – нормальными лекарствами. За неделю из 100 правильно лечившихся выздоровело 90 пациентов, а из 200 любителей шариков выздоровело лишь 150 (75%). А вот «тяжёлых» чаще лечили нормальными лекарствами: из 200 пациентов 150 принимали таблетки, 50 – гомеопатию. Из 150 лечившихся правильно за неделю выздоровела треть пациентов. А из 50 любителей гомеопатии выздоровело пять человек – всего 10%!
При этом, когда мы «смешиваем» тяжёлых и лёгких пациентов, выясняется, что гомеопатия помогла 155 людям, а лекарства – лишь 140. В общем, возникает парадокс Симпсона – когда при соединении разных массивов данных тенденция исчезает или меняется на противоположную. Этот же парадокс возникает, когда говорят: «От гомеопатии никто особо не умирает, а вот от обычной медицины только так пациенты гибнут». Но гомеопатией обычно не лечат переломы черепа, рак и гнойный перитонит – ей чаще всего лечат простуду. Не стоит манипулировать данными и сравнивать пациентов с насморком, которые и так поправятся через неделю, и пациентов с онкологией.
Кстати, вот недавний пример парадокса Симпсона: в Великобритании в какой-то момент смертность среди привитых от коронавируса стала выше, чем среди непривитых… Граждане забили тревогу: мол, смотрите, прививки убивают людей! Но на самом деле тогда в стране поголовно прививали стариков, инвалидов, пациентов с диабетом и раком. При этом не все здоровые и молодые британцы были привиты. Но антипрививочники, конечно, закрыли на этот факт глаза – и кричали про вред вакцин. Хотя исследователи, которые в той же Великобритании сравнивали привитых и непривитых из одной возрастной группы, выяснили: иммунизация снижает риск смерти.
Некоторые сторонники лженаучных идей иногда специально пользуются тем, что люди плохо ладят с теорией вероятностей. В той же Великобритании живёт парапсихолог Руперт Шелдрейк, автор книги «7 экспериментов, которые изменят мир». Руперт создал целый «научный метод» для доказательства экстрасенсорных способностей. Но секрет метода заключается в том, что Шелдрейк специально вносил в экспериментальные протоколы ошибки, которых наука пытается избежать. Это ошибки наподобие парадокса Симпсона — разные трюки при обработке данных, которые дают невероятные результаты.
Вот один из экспериментов, который описал парапсихолог. В нём участвовал человек с фантомной рукой (то есть человек, который лишился конечности, но по-прежнему её чувствовал). Доброволец должен был «положить» свою руку на одно из двух мест. При этом приглашённый экстрасенс пытался почувствовать, где же эта рука находится. Шелдрейк пишет: сначала маги не очень угадывали, где именно находится конечность, но со временем количество правильных ответов начало расти. «Значит, экстрасенсы чувствуют ауру тела!» -- пришёл к выводу мужчина. Можете сами повторить такой эксперимент и опровергнуть проклятую материалистическую науку! При это Шелдрейк описывает два важных условия, чтобы эксперимент с работал. Во-первых, «экстрасенсам» каждый раз надо сообщать, угадали они или нет. А, во-вторых, нельзя доверять управление фантомной рукой генератору случайных чисел, добровольцы должны сами решать, когда и как им руку двигать.
В чём тут фокус? Когда люди пытаются имитировать случайность, у них, как правило, не очень получается. Психолог Питер Брюгер обнаружил эффект «избегания повторений»: имитируя случайные броски кубика, человек будет стараться не называть шестёрку после шестёрки, пятёрку после пятёрки и так далее, хотя на самом деле вероятность выпадения того или иного значения от предыдущего броска не зависит. Причём этот эффект особенно сильно выражен у верующих в паранормальное, в меньшей степени у агностиков и в ещё меньшей у скептиков.
Поэтому и в эксперименте Шелдрейка человек с фантомной конечностью не будет двигать ей случайно, даже если захочет, а будет следовать неким собственным представлениям о вероятных паттернах. Если экстрасенсу каждый раз сообщать, прав он или ошибся, вскоре он начнёт «предсказывать» поведение добровольца, угадывать эти паттерны, делать похожие не случайные выборы. Вот и весь секрет. Шелдрейк сумел воспроизвести в реальном мире известную шутку математиков: «Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая!»
«Так, бабушка велела передать тебе: не надо ссориться из-за денег!»
Во многих компьютерных играх, где есть элементы случайности, разработчики специально придумывают «кармические кубики». Например, в «Baldur’s Gate III» игрокам постоянно надо подбрасывать двадцатигранные кубики – выпавшее число влияет на исход беседы, применение заклинания, изучение местности и так далее. Разработчики сделали так, что, если в предыдущий раз у пользователя выпало низкое значение на кубике, в следующий раз шанс успеха повысится (и наоборот) – таким образом у игроков не будет череды одних везений или сплошных неудач. Парадоксально, но подобная «неслучайность» лишь усиливает иллюзию случайности, подгоняя её под наши ожидания. Впрочем, в «Baldur’s Gate III» кармические кубики можно отключить – и тогда числа будут выпадать в соответствии с нормальной статистикой. Кстати, игра очень крутая – рекомендую.
Однажды я очень напугал свою бывшую девушку. Мы играли в такую игру: созванивались по ночам, она воображала какую-нибудь геометрическую фигуру – треугольник, квадрат или круг – а я угадывал, что моя девушка загадала. Я угадывал намного лучше, чем 1/3, предположительно потому, что мы оба избегали «случайных» повторений. Но моя бывшая девушка испугалась мистики и попросила прервать эксперимент.
Нашим плохим знанием теории вероятностей пользуются медиумы и фокусники. Так, в 2020 году вышла статья «Разговариваем с мёртвыми в школьном классе». Её авторы позвали в школу фокусника. Тот пришёл в класс и сделал вид, будто умеет говорить с покойниками. Фокусник называл имя умершего, а по реакции школьников понимал, кому из них мертвец приходится родственником. В итоге 65% подростков поверили, что к ним приходил настоящий медиум. Кстати, «медиумы» так и работают – по возрасту клиентов догадываются (иногда – со второй или третьей попытки), кто у них умер – мама, супруг или ребёнок. А потом говорят: «Так, бабушка велела передать тебе: не надо ссориться из-за денег! А ещё она тебя очень любит даже с того света». И люди такие: «Вау, как он догадался, что мы прямо сейчас делим наследство? Настоящий маг!» Но на самом деле после смерти родственников люди часто ругаются из-за финансов.
При этом после «сеансов» клиенты забывают об ошибках гадалок и медиумов. А вот если экстрасенс что-то угадал – это запоминается. В обычной жизни всё то же самое: мы обращаем внимания на «чудеса» и совпадения и совершенно не помним какие-нибудь несбывшиеся сны.
Приведу ещё один статистический трюк из арсенала «экстрасенсов». Представьте, что вы хотите разбогатеть. Вы можете взять базу людей, которые делают ставки на спорт – и разослать им бесплатные советы, на кого лучше поставить в ближайшем матче или лошадином забеге. Рекомендации вы можете взять из пула случайных исходов. Кому-то ваши советы «помогут» -- дайте этим счастливчикам ещё одни рекомендации на новый матч. Часть любителей ставок ваши советы снова выручат – тогда предложите им очередную консультацию, но уже за деньги. Или за долю от выигрыша. Есть вероятность, что люди согласятся, ведь они сами видели ваши «невероятные способности» на практике. Но на самом деле заниматься такими вещами я не советую – всё-таки деньги стоит зарабатывать честным трудом.
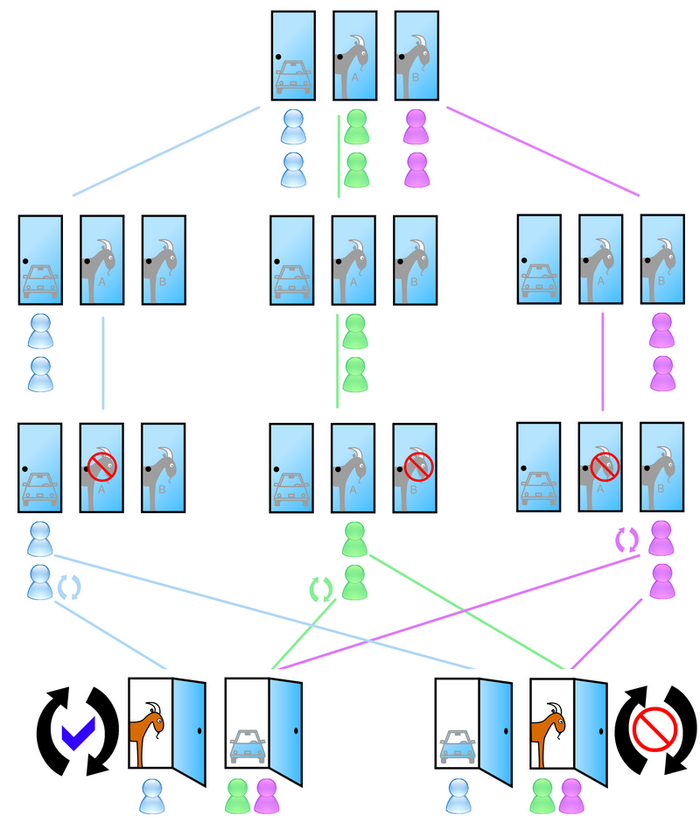
Ещё одна задачка: представьте, что вы попали на Страшный суд. Перед вами – три двери: за одной Рай, за двумя другими — бездна Ада. Когда вы выбрали (но не открыли!) дверь, Архангел, который знает правильный ответ, открывает одну из оставшихся дверей — и это обязательно дверь в Ад. После этого вам дают шанс сменить первоначальный выбор. Вы знаете, что Архангел всегда ведёт себя одинаково и честно. Если что, вы хотите попасть в Рай. Вопрос: что выгоднее — сменить выбор, оставить его прежним, или же разницы нет?
Чаще всего респонденты отвечают, что выбор неважен: шансы угадать нужную дверь в любом случае 50/50. Но оказывается, что, если изменить свой выбор, ваши шансы попасть в Рай повысятся в два раза! Как так? Дело в том, что вероятность отгадать дверь с первого раза — 33%. Поэтому, если не менять выбор, то шанс останется один к трём. Но, если поменять выбор, то шанс вырастает до 66%. Ведь с первого раза вы могли выбрать одну из двух неправильных дверей (шанс 2 к 3), и в обоих случаях попадёте в Рай — вторую неправильную дверь убрал Архангел. И только если вы изначально выбрали Рай, вы проиграете (шанс 1 к 3).
Возможно, у вас внутри всё восстаёт — как может измениться шанс, если я уже сделал выбор? — но объяснение станет гораздо нагляднее, если представить не три, а 1000 дверей. Тогда после вашего случайного выбора наш Архангел любезно убирает не одну, а 998 неправильных дверей. Изначально ваши шансы выбрать Рай были всего 1/1000. А после, если сменить дверь — в 999 случаях та дверь, которую НЕ выбрал Архангел, и ведёт в Рай.
Эта задача всегда вызывает огромный когнитивный диссонанс. Наверняка сейчас в комментариях появятся люди, которые скажут, что всё это чушь, вероятность составляет 1 к 2 и не меняется. Да, теория вероятности – это, повторюсь, очень контринтуитивная штука. А задачка про Гавриила – это вариант известного парадокса Монти Холла, только в оригинале речь шла не о Рае и Аде, а о машине и козах. Можете проверить, что ответ, данный выше, верен экспериментально. Мы с другом в свое время проверяли.
Мораль сегодняшнего поста проста: прежде чем считать что-то чудом, подумайте, не обманывает ли вас мозг. Теория вероятностей уж очень легко сбивает с толку. А если вас заинтересовала тема когнитивных искажений – советую пройти тематический курс, после которого, я уверен, вы больше никому не дадите себя обмануть. Жаль, что такому редко учат в школах.
P.S. Сегодня я предложил вам решить несколько задачек. Напоследок загадаю ещё одну, а ответы на неё пишите в комментариях. Итак, двум заключённым выдали по две монетки и рассадили в две разные башни. Каждый заключённый должен подкинуть свою монетку и угадать, что выпало на монетке товарища по несчастью. Тюремщики обещают, что, если хотя бы один заключённый даст правильный ответ, то обоих мужчин отпустят. В противном случае их обоих казнят. Коммуникация после броска невозможна, повлиять на бросок нельзя, но можно договориться о чём-то до начала испытания. Внимание, вопрос: существует ли способ, с помощью которого заключённые гарантированно выйдут на свободу?
Ответ на пост «Русское лото мошенничество на новый год»3
Результаты новогоднего розыгрыша: https://www.stoloto.ru/ruslotto/archive/1526
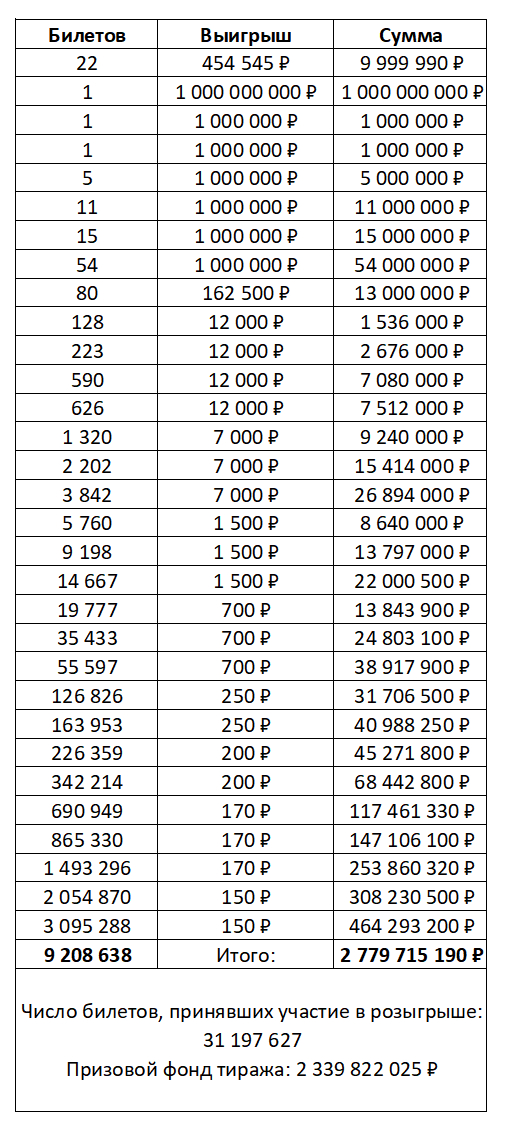
Давайте проанализируем эти данные — загоняем все в Excel и считаем
На сайте указано что призовой фонд тиража 2 339 822 025 ₽, а простое перемножение даёт сумму 2 779 715 190 ₽ — куда делись еще 439 893 165 ₽ ???
А теперь про вероятности: продано 31 197 627 билетов, из-них билетов с выигрышем 9 208 638, т.е. шансы 29,5% что вы ничего не проиграете и как минимум отобьете свою ставку.
Уберём мелкие выигрыши, оставим только билеты от 1500 р., т.е. с 10-кратным выигрышем — таких получается 38 746 штук.
(38746/31197627)*100 = 0,125%
Итого — вероятность выиграть что-то существенное всего 0,125%
Вероятность выиграть миллиард — 1 к 31,2 миллиону.
Но в любом случае эти вероятности значительно-значительно больше чем нам пытаются показать математики, когда считают комбинаторику — они рассматривают «сферическую лотерею в вакууме» получая совершенно нереальные цифры, но в новогоднем розыгрыше условия изменяются.
P.S. Можно сравнить с рулеткой в казино — ближайший пример получения 10-кратного выигрыша, это ставка на 2 числа с выплатой в 17:1. Вероятность выигрыша — 5.3%
Думайте сами, решайте сами — получается что подобный выигрыш в казино примерно в 40 раз более вероятен, чем в лотерею.
P.P.S. Азартные игры — зло.
P.P.P.S. Я лично знаю человека, который выиграл миллион в Русское лото. Они больше полугода получали эти деньги, заплатили с них налоги. Потом вкинули в покупку квартиры. Но для этого покупали билеты и играли каждую неделю чуть ли не с 1990-х годов.
Как ожидать неожиданное (2)
Продолжаем знакомиться с книгой Кита Йейтса.
Многие думают: «Совпадения не случайны». Это неудивительно, потому что большинство из нас, сознательно или нет, но считают, что являются центром Вселенной. Cмотрят на вещи со своей колокольни, объявляя удачу – судьбой. Даже там, где нет явной связи, ищутся и находятся знаки и смысл, например, в случае заболеваемости лейкемией в районах, прилегающих к линиям электропередач. Почему? Наверное, когда-то поспешные обобщения спасали нам жизнь. Если кто-то шумит в кустах – то это может быть хищник. Может и не быть, только лучше всё-таки дёрнуть подальше оттуда.
Смысл находим и потому, что не совсем хорошо представляем себе картину случайности. Считаете, эти птицы гнездуются в хаотичном порядке?
Нет, конечно. Им и в голову не придёт в голову усесться совсем рядом с соседом. А должны бы, если бы садились в случайном порядке.
Ну а если случайная картина напоминает что-то, то мы считаем часто, это не может быть случаем. Этот психический феномен называется апофенией. Некоторые проводят время жизни в поиске тайных сообщений, проигрывая популярные треки задом наперёд, ищут потусторонние сообщения в шуме из динамика радиоприёмника и жалуются на Джоббса, который, по их мнению, недостаточно тщательно перемешивал треки на Айподе. Пришлось тому переделывать алгоритм, чтобы не попадалось несколько треков одного и того же исполнителя подряд (хотя по канонам случайности это вполне возможно).
На самом деле, если захочешь увидеть какое-то совпадение – непременно найдёшь. Учёные, не найдя искомой корреляции в наборе данных, частенько занимаются p-hacking или подгонкой результата. Я рассказывал об этом здесь. Ищут какие-то другие корреляции. И находят их. А то, что они являются полной экзотикой и не воспроизводятся – не волнует. Главное, что можно статейку тиснуть.
В Британии, начиная с 1966 года, было организовано Бюро Предсказаний, куда можно позвонить и рассказать о приближающемся несчастье. В 1967 году некто Алан Хенчер сообщил о скором падении самолёта в горах со смертью 123 или 124 человек. На следующий день мир облетела весть о катастрофе пассажирского лайнера, попавшего в грозу над Кипром. 124 смерти. Бинго! Или нет? Начнём с того, что Кипр горами назвать трудно. Далее, ещё два человека умерло через пару дней в больнице. И закончим тем, что это был лишь один из сотен звонков, поступивших в Бюро от Хенчера. Совпадение? Вполне может быть.
С по-настоящему большими числами всяко бывает. Бывает, выигрывают в лотерею два раза подряд. Бывает, выпадают одни и те же числа два тиража подряд, как в болгарской «6 из 42» в сентябре 2009 года. При этом если в первом из них шесть номеров не угадал никто, то во втором – аж восемнадцать человек. Бывает, чо. Вписать уже выпадавшие номера в билет для следующего тиража – вполне известная стратегия. А вероятность повтора комбинации за более, чем полувековую историю болгарской лотереи составляет ни много, ни мало – 94%. Несмотря на это, болгарский министр спорта запустил расследование, которое не нашло нарушений. Что не удивляет. Не должно удивлять.
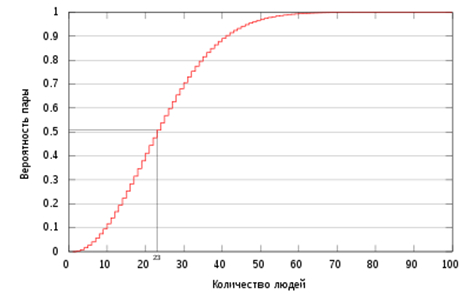
Как не должны удивлять повторяющиеся дни рождения в классе, начиная с 23 человек. Да, начиная с этого размера, вероятность того, что у кого-то с кем-то совпадёт, превысит 50%. Объясняется это значительным превышением числа возможных пар (253) таких совпадений над числом одноклассников.
У группы в полсотни человек она составит 97%. А какова она будет у четырехста? 99,99999999...? Нет, конечно. Все 100%. В году-то не бывает больше 366 дней. «Элементарно, это же принцип Дирихле», – скажет математик. «Здравый смысл!» – ответит обыватель. Когда мест в автобусе меньше, чем пассажиров, кому-то придётся стоять.
Как видим, события, которое, казалось бы, имеют весьма малые шансы случиться, происходят вокруг нас постоянно. Здесь ключевые слова: «казалось бы».
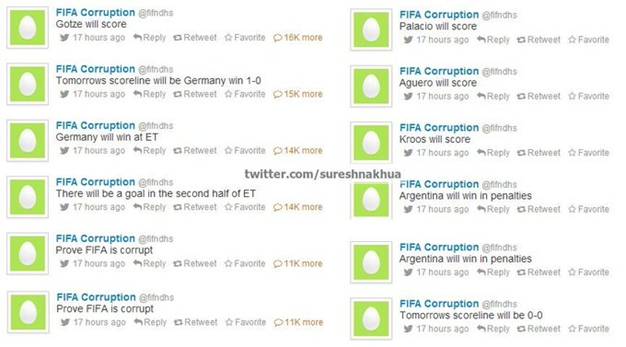
Принципом Дирихле пользуются некоторые манипуляторы, пытаясь создать иллюзию своей всеведущести. Они делают прогнозы, закрывающие все возможные варианты с тем, чтобы стереть всё несбывшееся после события. Так сделал некто fifNdhs в Твиттере в попытке «вскрыть» коррупцию в ФИФА.
Нечто похожее может произойти без манипуляций. Мы можем восхищаться устойчивостью старых зданий, простоявших столетия без видимых повреждений. Но при этом забываем, что всё неустойчивое уже давным-давно развалилось. Можем пасть жертвой рекламы какого-нибудь лекарства, ссылающегося на публикации о его успешном применении. Но забываем, что неуспешные применения вообще не публикуются. Это искажение называют парадоксом выжившего. Совет автора читателю: будьте подобны Шерлоку Холмсу, который делал выводы не только из очевидного, но и из отсутствующих свидетельств. Обращать внимание, когда собаки не лают в ночи.
Мы плохо справляемся с неопределённостью. Нам трудно заставить себя заполнить лотерейный билет так, чтобы какие-нибудь два числа шли друг за другом, хотя примерно половина тиражей содержит такие пары. Хотите создать по-настоящему случайную последовательность? Не выдумывайте ничего, а просто бросьте жребий. Лучше получится. Опытные игроки в камень-ножницы-бумагу безошибочно определяют любую стратегию и начинают бить тебя, как только отгадают её. Не проиграть им можно, лишь переключившись на чистый случай в своём выборе. Так и всюду: если мы на самом деле хотим избежать эксплуатации своей предсказуемости, то некоторую часть своего процесса принятия решения можно попытаться отдать на волю случая.
Некоторую, но не всю! В мире достаточно идиотов, принимающих все решения по броску монеты. Более разумной является смешанная стратегия, которую используют, например, индейцы на востоке Канады. Они бросают жребий, чтобы определить, куда пойти охотиться следующий раз. Случай может помочь нам и при аналитическом параличе, когда мы не можем решиться выбрать из множества альтернатив. Например, выбрать блюдо в меню ресторана. Поговорку «лучшее – враг хорошего» не просто так придумали. Порой, важнее сэкономить время и быстро определиться, чем его упустить в погоне за сомнительной выгодой.
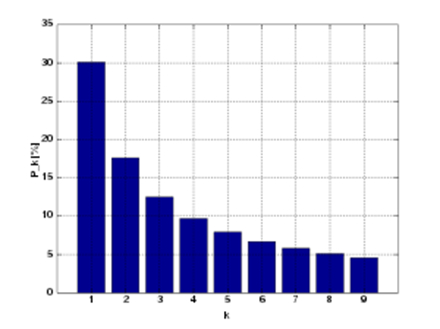
Наше неумение понимать неопределённость можно использовать для изобличения манипуляций. Откройте свою адресную книгу, и если она достаточно велика, можете убедиться, что первой цифрой в номерах домов чаще бывает единица, за ней идёт двойка и т.д. Девятка попадается реже всех. Хоть первым подобный факт заметил американский астроном в девятнадцатом веке (он заметил, что первые страницы математических сборников таблиц всегда наиболее истрёпаны), закон получил имя Фрэнка Бенфорда, который обнаружил подобное распределение в списках бассейнов рек, значениях теплоёмкости и прочих таблицах, включая номера домов.
Казалось бы, просто забавный факт, но нет. Не забываем, что случайные данные тоже подделывают, и не всегда в благих целях. Так некто Уэйн Джеймс Нельсон обналичил как минимум 23 фальшивых чека на сумму до двух миллионов долларов. Жулик знал, что всё, что не превышает стотысячную отметку, практически не проверяется. Но его подвела жадность: слишком многие из его сумм начинались на девятку.
Можно вспомнить в этой связи более общий закон Ципфа, согласно которому частота появления какого-то слова из текста обратно пропорциональна его порядковому номеру в списке «популярности». Наиболее популярное в английских текстах слово „the“ попадается гораздо чаще второго по популярности „of“ и ещё гораздо чаще остальных слов.
Подобным образом разбросаны и другие феномены, например, сила толчков землетрясений в регионе. 4 февраля 1974 года после предупреждения центра землетрясений одной из провинций на северо-востоке Китая власти начали массовые эвакуации. И не зря: в 19:46 случился толчок магнитудой в 7,5 баллов. Сотни тысяч жизней оказались спасены. Китай с гордостью заявил на весь мир об успехах своих сейсмологов. Вот только успехи эти оказались ограничены. Пару лет спустя в соседней провинции случилось ещё одно землетрясение силой в 7,6 баллов. 242 тысячи погибших. Никто не смог предсказать. На что же опирались предсказатели в 1974 году? На правило из старой рукописи, гласившее: «избыток дождя осенью непременно приведёт к землетрясению зимой». Если учесть, что 4 февраля – последний день зимы по китайскому календарю, а также пятибалльный форшок утром того же дня, то нетрудно понять логику китайского сейсмолога, забившего тревогу. Ему повезло. Но всё же он не был так уж неправ в своих ожиданиях. Он мог рассчитывать на сильное землетрясение в регионе в определённый промежуток времени согласно закону Гутенберга-Рихтера. Мы по-прежнему не можем заранее знать, когда это случится, но можем оценить вероятность такого события в определённый промежуток времени. И заранее инвестировать в строительство сейсмоустойчивых зданий, например.
Неочевидность вывода может поджидать нас в, казалось бы, простых случаях. К примеру, при известном заблуждении прокурора, при котором какая-нибудь улика интерпретируется против обвиняемого на том основании, что она является естественным результатом его возможных действий. Но на самом деле она может быть результатом и действий других лиц. Пусть даже эти лица с меньшей вероятностью способны создать её, но круг их может быть так широк, что в целом такой вариант может стать более вероятным, чем тот, что предлагает прокурор. Актуальной иллюстрацией может служить недавняя пандемия коронавируса, когда все массово тестировались. Если тест оказывался позитивным, то это не значило автоматически, что тестируемый инфицирован. Ведь при невысоком уровне распространения вируса в целом и повальном тестировании гораздо выше была вероятность ложнопозитивного теста. Здесь мы входим в мир условной вероятности и формулы Байеса, по которой вероятность можно уточнить на основе новых данных.
Отсюда мораль: при выводе о возможной причине явления нужно обязательно учитывать все возможные сценарии и их вероятности. Иначе можно легко пасть жертвой предвзятости подтверждения. Необходимо собирать новые данные, крупицу за крупицей. И кто знает, может, наступит момент, когда придётся изменить своё мнение. Это нормально. Так Байес сам открыл свою формулу, практикуясь на бильярдном столе и считая шары, попавшие в один или другой угол.
Пожалуй, логичнее можно было бы называть книгу «Занимательная теория вероятности». Слишком велико желание автора набросать побольше иллюстраций из этой науки, приправив соусом из баек о мошенниках. И всё же, до сей поры какая-никакая, но связь повествования с предвидением имелась. В случае с теорией игр, о которой автор рассказывает в очередной главе, я её не увидел.
Вероятность
Вероятность иногда выделывает странные штуки.
Когда мы проходили тервер, в аудитории находилось 12 человек, включая нашего препода Михаила Петровича Гордина (низкий ему поклон).
Михаил Петрович сказал: "Нас здесь ровно двенадцать, так что по теории вероятностей я предсказываю, что как минимум у троих совпадёт месяц рождения. Давайте, назовите месяц своего рождения!"
Как уже понятно, все присутствовавшие родились в разные месяцы.
"Ну и группа у вас!", - заметил Михаил Петрович. - "Первый раз с такой сталкиваюсь!"
Тут я кое-что вспомнил.
"Вы знаете, у нас в группе у всех и имена разные!"
Да. В группе из двадцати одного человека не было совпадающих имён!
PS: А ещё однажды, исследуя гиперболоиды, и взяв коэффициенты "с потолка", Михаил Петрович получил две плоскости.
UPD: Просто имена. Без фамилий. Вспомнил всех.
Денис Алевтина Ольга Юлия Наталья Анна Эльвира Елена Роман Илья Владимир Вадим Николай Сергей Александр Андрей Игорь Олег Станислав Михаил Ромас Александр
Почему серьёзные дяди не играют в Монополию?
Монополия, ровно как и Миллионер, и все подобные им настольные игры, исход которых зависит от суммы результата выброшенных игральных костей - это игры, победу в которых легко предсказать.
Почему?
На этот вопрос ответит кривая Гаусса и закон равномерного распределения - потому что.
Для доказательства предсказуемости исхода, я не поленился 20 лет подряд играть в Монополию и 100 раз подбросить пару игральных костей, а потом 200… 400… 1000 раз. Шутка!
Рубрика э-э-эксперименты
На самом деле достаточно сотню раз подбросить кубики, чтобы убедиться в истинности равномерного распределения, а именно, что кривая Гаусса работает.
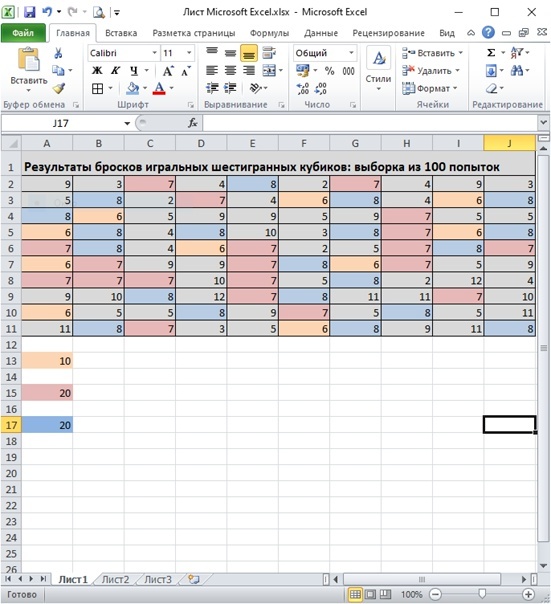
В данной таблице я записывал результаты получаемые, каждый раз после броска двух кубиков. Как видно числа 6, 7, 8 (результаты суммы) забирают себе 50% от всех результатов.
Предлагаю немного разобраться почему же так вышло. Возьмите листочек бумаги и ручку - будет интересно! А если не взяли, то я все равно приложу скриншот моих измышлений в виде еще одной таблички.
Итак.
Допустим, что у нас есть два игральных кубика с шестью гранями каждый. Если рассматривать каждый из кубиков индивидуально, то вероятность выпадения любой из шести граней равняется 16,(6)%, все поровну и при должной выборке мы выясним, что так и есть.
Но, вот, что получается, если мы добавляем второй игральный кубик… давайте запишем на листочке все возможные комбинации сумм пары чисел от 1 до 6 (иначе говоря, какие грани нужно сложить на кубике), чтобы получилось нужное число… 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Оп-оп-оп, а что это у нас такое? А это у нас уже знакомая нам фигура, чем-то очень напоминающая кривую Гаусса… ой, это же и есть она!
Так устроена вероятность, что вы неизбежно большее количество раз за всю игру выбросите числа 6, 7 и 8 просто из-за того, что их представление использует суммы максимального количества граней кубика. Это значит, что они будут попадаться вам чаще всего с вероятностью не менее, а то и более чем 50%. Исходя из этого, не хитрым способом можно предсказать выигрышную стратегию любой игры опирающейся на результат суммы броска N-го количества игральных костей, но нас, в рамках данной статьи интересует Монополия и иже с ней.
Разрабатываем стратегию
Игровое поле Монополии - это квадрат 11 на 11 (иногда больше, иногда меньше), где угловая клетка является общей для двух прилегающих к ней граней.
Если мы применим к этим данным известное нам извыше, то можем с уверенностью сказать, что с большей долей вероятности наша фишка попадет на клетки №6, 7 и 8. В следующий этап броска кубика мы вероятнее всего попадем на клетки №13, 14, 15. Далее клетки №20, 21, 22 и №27, 28, 29, после этого №34, 35, 36, и, наконец №40, 1, 2 - первый круг окончен!
Заметьте, что уже на первом круге вы дважды оказались в зоне клеток 20-30, а чем дальше зайдет игра, тем чаще вы там будете оказываться. С высокой долей вероятности можно предположить точное расположение вашей фишки и фишек соперника, зная очередь в которую был выброшен кубик.
Смею предположить и проверял, что едва ли не единственной стратегией позволяющей выиграть в Монополию является выкуп улиц расположенных в диапазоне клеток 20-30, после чего можно медленно наслаждаться поражением соперника(ов) по игре, исполнить предначертанное названием игры, став монополистом, и выкупить все улицы и соперника, окончательно его обанкротив.
ВСЁ! ВСЕМ СЧАСТЛИВОГО НОВОГО 2024 ГОДА И ХОРОШИХ ВЫХОДНЫХ!
Ложный вывод монте карло
Ложный вывод монте карло
Исход случайного события не зависит никак от прошлых попыток.
А что если?)
Вот находят археологи древний артефакт, с надписью и начинают описывать. Это была вещь для такого-то обряда, использовали его так. Но на деле, это какая-нибудь антистресс игрушка или модная безделушка с (Шелковый Путь)АлиЭкспресса. А письмена что написаны. Это описание, состав и предназначение, инструкция по применению. И адрес типа такого, но на древнем языке?)