Квантовые вычисления без ошибок: новый шаг к надежным логическим операциям
Автор: Денис Аветисян
От автора: Заранее извиняюсь, что не получилось привести формулы целиком - Пикабу не умеет отображать формулы в LaTeX формате, а ссылку на полный обзор в моём блоге запрещают модераторы.
Исследователи продемонстрировали эффективный способ реализации универсальных квантовых операций, устойчивых к ошибкам, в перспективных кодах поверхностного типа с улучшенной скоростью передачи данных.
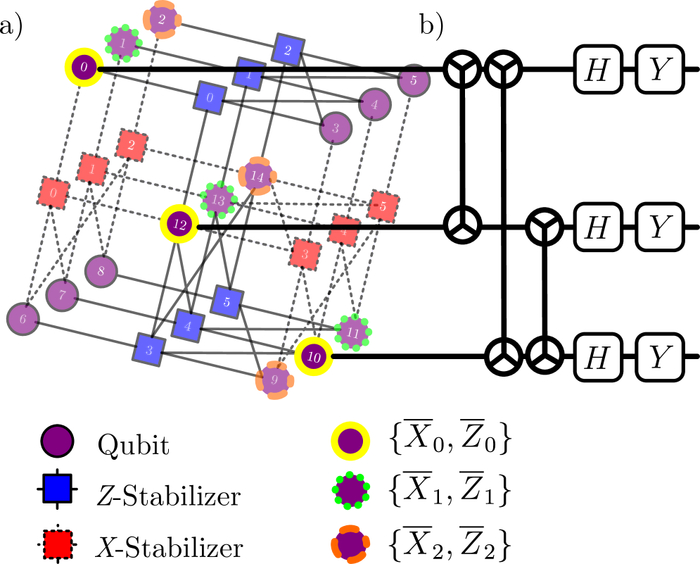
Код поверхностной коррекции ошибок, основанный на графе Таннера для конфигурации ⟦15,3,3⟧, демонстрирует взаимосвязанные копии кодов с d=2 и реализует логический гейт H посредством кругового обмена, включающего все-к-все взаимодействия Y и поперечные гейты H и YY на кубитах, поддерживающих логический оператор, что позволяет реализовать устойчивую к ошибкам логическую схему.
Предложена конструкция высокопроизводительных логических вентилей для кодов с лифтовой связностью, обеспечивающая управляемый расход ресурсов и приближающая возможность создания масштабируемых квантовых компьютеров.
Несмотря на перспективность кодов с низкой плотностью проверки чётности (qLDPC) для создания отказоустойчивой квантовой памяти, их вычислительная сложность остаётся существенным препятствием. В работе, озаглавленной 'Addressable fault-tolerant universal quantum gate operations for high-rate lift-connected surface codes', представлен подход к реализации универсальных отказоустойчивых квантовых операций на недавно разработанных кодах с лифтовой связностью (LCS). Показано, что предложенные схемы логических вентилей, основанные на флаговых кубитах, достигают псевдопорогов в диапазоне 4.8· 10⁻3-1.2· 10⁻2 для шума на уровне схемы. Сможет ли этот подход обеспечить практичную реализацию отказоустойчивой квантовой логики в кодах qLDPC с высокой скоростью передачи данных и открыть путь к созданию масштабируемых квантовых компьютеров?
Хрупкость квантовых вычислений: путь к надежности
Квантовые вычисления обещают экспоненциальное ускорение решения сложных задач, однако фундаментальная природа кубитов делает их крайне чувствительными к возмущениям и склонными к ошибкам. Создание отказоустойчивого квантового компьютера требует преодоления декогеренции и несовершенства квантовых вентилей. Традиционные методы коррекции ошибок в квантовых системах влекут за собой значительные вычислительные издержки, существенно ограничивая масштабируемость. В связи с этим, разработка инновационных подходов к квантовой коррекции ошибок является ключевым фактором для реализации практических квантовых компьютеров, способных решать задачи, недоступные классическим вычислительным машинам, и открывает перспективы для революционных изменений в различных областях науки и техники, от материаловедения до фармацевтики и искусственного интеллекта. Эффективные стратегии коррекции ошибок, минимизирующие накладные расходы и позволяющие сохранять квантовую информацию в течение длительного времени, представляют собой центральную задачу современной квантовой информатики.
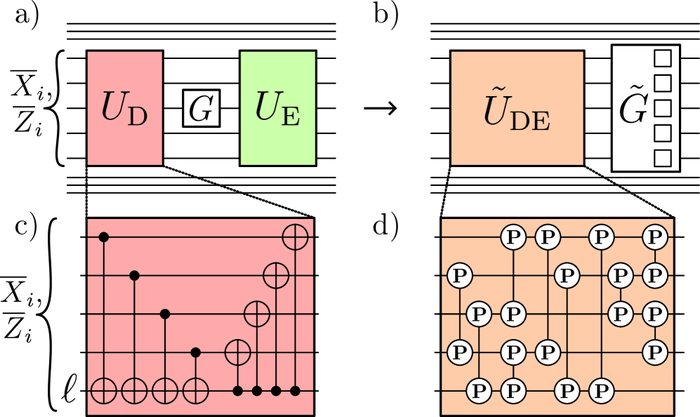
В конструкции круговых ворот используется декодирующая схема, отображающая логические кубиты на физические, за которой следует применение ворот и обратное кодирование, при этом критическим узлом является возможность распространения ошибок через эту схему. Для обхода этого ограничения ворота переносятся в конец схемы кодирования, что приводит к адаптированной схеме и преобразованным воротам, которые становятся трансверсальными для однокубитных клиффорд-ворот. Эффективной реализацией декодирующей схемы является использование вентилей CNOT, отображающих логические операторы на один физический кубит, а перенос однокубитных клиффорд-ворот через схему перекодирования приводит к схеме, состоящей из вентилей Pauli-controlled-Pauli, применяемых ко всем парам кубитов.
Квантовая Защита: Коды и Трансверсальная Реализация
Квантовые коды коррекции ошибок обеспечивают избыточное кодирование квантовой информации, позволяя обнаруживать и исправлять неизбежные ошибки, возникающие в процессе вычислений. Особое внимание уделяется топологическим поверхностным кодам, в частности, кодам, связанным подъемными путями, благодаря их внутренней устойчивости к локальным возмущениям. Трансверсальная реализация предоставляет возможность применять клиффорд-вентили к закодированным кубитам без распространения ошибок, значительно упрощая процесс коррекции. Тем не менее, реализация не-клиффорд-вентилей, необходимых для осуществления универсальных квантовых вычислений, по-прежнему представляет собой сложную задачу, требующую дальнейших исследований и инновационных подходов к управлению квантовыми состояниями и минимизации ошибок в квантовых схемах.
Целевые логические Клиффордовские гейты для кодов ind=3d=3LCS реализуются посредством все-к-все операций YCY для гейта H-overline, ZCZ для гейта S-overline и операций CX для внутриблочного гейта CiXj-overline, что демонстрирует специфическую структуру операций, необходимую для реализации этих гейтов в данной кодовой структуре.
За пределами поперечности: Флаг-кубиты и не-поперечные гейты
Реализация универсальных квантовых вычислений посредством не-поперечных схем представляет собой перспективный подход, однако сопряжена с задачами контроля распространения ошибок. Для решения этой проблемы разрабатываются конструкции, основанные на измерениях флага и использовании флаг-кубитов, позволяющие аккуратно управлять распространением ошибок в квантовой системе. Каскадное соединение (конкатенация) становится ключевым инструментом для обеспечения устойчивости к ошибкам даже в не-поперечных схемах, открывая путь к надежным квантовым вычислениям. В рамках этой схемы особую роль играют PCP (Pauli-Controlled-Pauli) гейты, являющиеся фундаментальными строительными блоками для реализации сложных логических операций, необходимых для эффективной коррекции ошибок и надежной работы квантового компьютера.
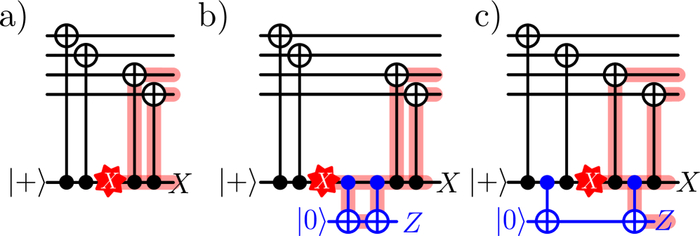
В ходе исследования было показано, что введение дополнительного флагового кубита позволяет выявлять коррелированные ошибки, возникающие при Pauli-XX-измерении, путем коммутации одной операции через вторую CXCX, что приводит к регистрации ошибки только на флаговом кубите и позволяет избежать ее распространения на кубиты данных.
Квантовая устойчивость: взгляд сквозь схему
Формализация устойчивости к ошибкам в квантовых вычислениях осуществляется посредством рассмотрения результатов детектирования как ограничений, накладываемых квантовой схемой. Расширение этого подхода, включающее пространственно-временные коды и модели детекторов, позволяет глубже понять механизмы распространения и коррекции ошибок. Мощным инструментом для представления этих сложных схем служат паутинные диаграммы Паули – тензорные сети, визуализирующие взаимосвязи между кубитами и операторами ошибок. Развитие алгоритмической и гаджетной устойчивости к ошибкам предлагает инновационные стратегии для повышения надежности квантовых вычислений, позволяя создавать более устойчивые к помехам схемы и алгоритмы, способные эффективно исправлять ошибки, возникающие в процессе работы с n-кубитными системами.
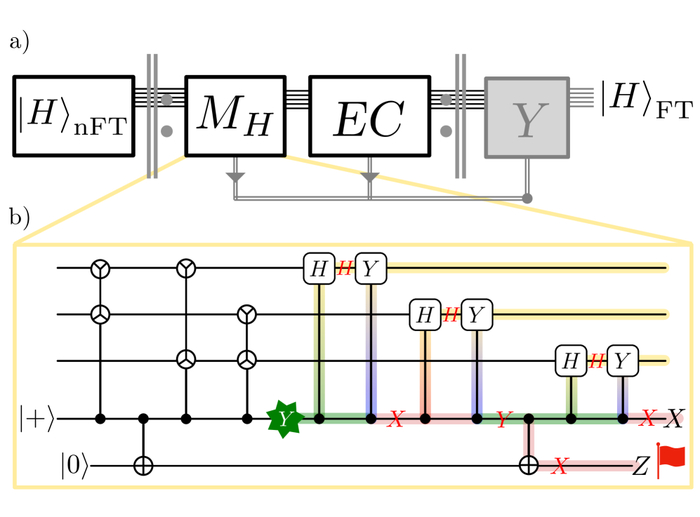
Разработана схема устойчивого к ошибкам приготовления магического состояния, использующая логические блоки для выполнения протокола как в детерминированном режиме, так и по принципу повторения до успеха, при этом для устойчивого приготовления одного магического состояния требуется повторение измерения логического оператора Адамара и коррекции квантовых ошибок до получения однозначно интерпретируемого результата, а в случае обнаружения ошибки применяется логический оператор YY-flip, при этом измерение целевого логического оператора Адамара на трех физических кубитах данных, поддерживающих логические операторы X̄ᵢ, Z̄ᵢ, использует вспомогательный кубит для обнаружения опасных ошибок, которые могут проявиться как логические XX или ZZ на кубитах данных, не изменяя состояние измерительного кубита.
Предел Шума и За Его Границами: Определение Надежности Квантовых Кодов
Для оценки эффективности кодов квантовой коррекции ошибок ключевым показателем является так называемый псевдопороговый уровень (10⁻3 для алгоритмической отказоустойчивости и 10⁻4 для отказоустойчивости, основанной на гаджетах), определяющий уровень шума, при котором механизмы исправления ошибок начинают эффективно функционировать. В данной работе исследуются коды qLDPC, представляющие собой перспективные решения для создания высокоскоростных кодов с уменьшенными требованиями к количеству кубитов. Стабилизаторы, являющиеся фундаментальными компонентами при определении и реализации этих кодов, тесно связаны с логическими операторами, определяющими пространство ошибок и обеспечивающими проверку корректности процесса коррекции. Достижение указанных псевдопороговых значений демонстрирует значительный прогресс в создании жизнеспособных систем отказоустойчивых квантовых вычислений.
Предложенный отказоустойчивый протокол коррекции ошибок позволяет однозначно идентифицировать до 𝒪(p) ошибок посредством измерения генераторов стабилизаторов с флагами, при этом последующее измерение без флагов обеспечивает шумостойкий раунд стабилизационных измерений, а при отсутствии ошибок или наличии некорректируемых ошибок дальнейшие действия не требуются.
Исследование демонстрирует, что достижение универсальных, отказоустойчивых квантовых вычислений в кодах поверхности требует не просто разработки алгоритмов, но и глубокого понимания взаимосвязей между ресурсами и производительностью логических вентилей. Авторы статьи предлагают конструкцию высокопроизводительных логических вентилей с управляемыми накладными расходами, что является ключевым шагом к практической реализации квантовых вычислений. В этом контексте уместно вспомнить слова Вернера Гейзенберга: «Самое важное — не то, что мы знаем, а то, что мы еще не знаем». Это отражает суть квантовых вычислений – постоянное исследование границ возможного и выход за рамки классического понимания, подобно взлому системы ради понимания её устройства.
Что дальше?
Представленная работа, хотя и демонстрирует конструкцию логических вентилей с управляемыми накладными расходами в кодах с поверхностным соединением, лишь приоткрывает дверь в лабиринт. Истинная проверка не в элегантности реализации, а в её устойчивости к непредсказуемому шуму реальности. Стремление к “псевдопороговой” ошибкоустойчивости – это не финишная прямая, а скорее указатель на необходимость постоянного пересмотра самих принципов кодирования.
Очевидно, что узким местом остается масштабируемость. Увеличение размера кодированного пространства неизбежно выявляет скрытые зависимости и нелинейности, требующие новых математических инструментов для анализа и оптимизации. Следующим шагом видится не просто уменьшение накладных расходов, а разработка принципиально иных архитектур, способных к самовосстановлению и адаптации к меняющимся условиям. В конечном счете, вопрос не в том, как построить идеальный код, а в том, как заставить несовершенную систему работать.
Впрочем, не стоит забывать, что хаос – не враг, а зеркало архитектуры, отражающее скрытые связи. Попытки полностью подавить шум обречены на провал. Гораздо перспективнее научиться использовать его как ресурс, превращая случайные флуктуации в инструмент для вычислений. И тогда, возможно, квантовый компьютер перестанет быть мечтой о совершенстве и станет отражением самой реальности – несовершенной, непредсказуемой, но удивительно красивой.
Оригинал статьи: https://arxiv.org/pdf/2511.10191.pdf
Связаться с автором: linkedin.com/in/avetisyan