Математика: почему математические формулы работают в реальном мире?
Мы привыкли считать математику просто счётом, но она умеет предсказывать движение планет и поведение атомов. Удивительно: мозг, который эволюционировал для охоты и сбора ягод, придумал язык, которым «говорит» сама Вселенная. Почему это вообще возможно — открытый вопрос, который волнует и физиков, и философов, и психологов.
Физик Юджин Вигнер назвал это «непостижимой эффективностью» математики. Мы не просто описываем природу — мы угадываем её на шаг вперёд, и угадываем с точностью до десятого знака. При этом никто не может объяснить, почему человеческие символы так точно ложатся на реальность. Математика скорее как фонарь: она не только показывает путь, но и сама создаёт то, что мы называем реальностью.
Как древние мыслители искали истину и почему это важно для нас сегодня
Древние греки впервые задали вопрос: «Как узнать, что мир вокруг нас настоящий?» Их ответы разошлись так сильно, что спор продолжается до сих пор.
Гераклит сравнивал жизнь с рекой: вы не войдёте в одну и ту же воду дважды — всё меняется каждую секунду. Эпикур, наоборот, верил глазам и рукам: если камень твёрдый, значит, он и есть твёрдый. Платон пошёл дальше всех: он сказал, что деревья, дома и даже звёзды — это лишь тени на стене пещеры, а настоящий мир скрыт от глаз и доступен только уму. Поэтому он считал математику важнее наблюдений: не нужно считать видимые звёзды, нужно думать о идеальных кругах, по которым они «должны» двигаться.
Аристотель вернул людей на землю. Он показал, что мы сами выдумываем слово «треугольность», после того как увидели десятки разных треугольников. Знание растёт из жизни, а не из небес. Его идеи прожили тысячу лет, пока в XVII веке Рене Декарт не поднял новый вопрос: «А не обманывают ли нас чувства?» Его ответ был хитрым: пока я мыслю, я точно существую. А раз я ограничен, значит, есть и совершенное существо — Бог. А Бог, по Декарту, не станет нас обманывать, значит, мир всё-таки реален.
Практический вывод: когда вы сомневаетесь, правда ли то, что видите, — проверьте. Спросите себя: «Откуда я это знаю? Видел сам? Проверил? Или просто услышал?» Древние учили: истина либо в постоянном изменении, либо в чувствах, либо в разуме. Современный человек добавляет: истина ещё и в повторной проверке.
Как мозг узнаёт мир: три истории о том, откуда берутся идеи
Декарт: мир — часы, мысль — математика
Рене Декарт сказал: «То, что можно измерить (длина, форма, движение), — реально. Цвет и запах — всего лишь ощущения». Он представлял природу огромным механизмом, который работает по математическим законам. Опыты он ставил, но считал, что главное — логические расчёты, а не пробирки.
Гоббс: всё из плоти, даже мысль
Томас Гоббс пошёл дальше: «Вне нас — только движущаяся материя». Ощущения возникают, когда тела давят на органы чувств. Мозг складывает образы, как кубики: образ яблока → образ дерева. Слово «треугольник» — это ярлык на коробке с памятью обо всех увиденных треугольниках. Математика, по Гоббсу, — единственный надёжный способ упорядочить эти образы и получить истину. Такая жёсткая идея шокировала даже математиков: «Получается, без формул не понять ни Бога, ни душу?»
Как мыслят философы: от Локка до Беркли
Локк считал, что человек познаёт мир тремя путями.
Первый — прямая интуиция: «я мыслю, значит, я существую».
Второй — рассуждение: шаг за шагом соединяем идеи и видим, согласуются ли они (как в геометрии).
Третий — чувства: глаз, ухо, кожа подсказывают, что вне нас есть вещи.
Когда математика спорила с Богом: как философы проверяли, что реально
Беркли: «Ваши формулы не лучше молитв»
Философ Джордж Беркли в 1734 году устроил математикам разнос. Он спросил: «Вы говорите о мгновенных скоростях, но что это такое? Это ни число, ни ноль. Получается, вы верите в призраков величин». Его главная мысль была простой: если математики критикуют религию за невидимые вещи, пусть сначала объяснят, во что сами верят. Беркли считал, что весь мир — это лишь картинки в сознании Бога и людей. Стол существует, пока его кто-то видит.
Юм: «А я сомневаюсь даже в себе»
Шотландец Дэвид Юм пошёл дальше. Он сказал: «Мы не знаем ни материи, ни разума. Есть только ощущения: тёплая чашка, звук дождя, запах хлеба». Всё остальное — удобные ярлыки. Пространство и время тоже не вещи, а способ, как мы складываем воспоминания. Закон «солнце всходит» — просто привычка: вчера встало, позавчера встало, но гарантии, что завтра встанет, нет. Даже «я» — это не душа, а цепочка ощущений, как бусины на нитке.
Как Кант спасал разум от Юма и почему он «придумал» евклидову геометрию
Юм сказал: «Мы ничего не можем знать наверняка – ни Бога, ни причин, ни самого мира».
Кант ответил: «Нет, разум всё-таки способен к истине, и я покажу, где он её берёт».
Что Кант считал настоящим знанием
- Аналитические фразы («все тела протяженны») ничего нового не сообщают – это просто раскрытие слов.
Как философы объясняли, откуда мы знаем о мире
Кант: разум расставляет мебель, а чувства приносят гостей
Иммануил Кант считал, что законы Ньютона и геометрия Евклида встроены в наш разум. Мы будто бы родились с готовыми полками: пространство, время, причина. Внешний мир приносит только «сырой материал» – цвета, звуки, запахи. Разум сразу раскладывает этот хлам по полочкам, и получается научная картина. Сам мир «в себе» мы никогда не увидим: можем знать лишь то, как он укладывается в наш встроенный шкаф. Когда появляются новые науки, человечество не открывает новые законы, а просто открывает новые ящики своего интеллекта.
Милль: все знание – как кулинарный опыт
Джон Стюарт Милль спорил: полок нет, есть только повар-кулинар – наш опыт. Мы пробуем яблоко, потом второе, замечаем, что 2+2=4, и делаем обобщение. Даже аксиомы геометрии – это «рецепты», выученные на опыте: нам просто так часто встречались прямые линии, что мы решили: они всегда пересекаются в одной точке. Внешний мир для Милля – это «поваренная книга», которая продолжит работать, даже если все повара исчезнут. Мы не видим саму книгу, но постоянно пробуем блюда и составляем меню. Наши рецепты никогда не бывают точными, но ими можно пользоваться: мосты не падают, самолёты летают.
Почему наши глаза нас обманывают
Мы привыкли доверять глазам, но зрение постоянно врёт. Это не просто любопытный факт — понимание обманов чувств помогает не наделать ошибок в жизни и научиться проверять свои впечатления.
Глаза рисуют неверную картину
Возьмите две одинаковые линии. Добавьте к одной стрелки наружу, к другой — внутрь. Первая кажется длиннее: это иллюзия Мюллера-Лайера. Такие «фокусы» показывают, что мозг «додумывает» глубину и объём там, где их нет. Та же приём используют художники: на плоском холсте они рисуют уходящие вдаль рельсы и ящики меньшего размера, и мы видим трёдную сцену. Картина Рафаэля «Афинская школа» работает именно благодаря этому обману.
Почему Луна у горизонта кажется гигантской
...
Как мозг обманывает нас каждый день
Наши глаза, уши, кожа и язык не показывают мир таким, какой он есть. Они подают «сжатую картинку», удобную для жизни, но далёкую от физической правды.
Цвет, твёрдость, тепло — это не свойства вещей, а наши выдумки
- Белый предмет просто отражает весь свет, а коричневый — лишь часть его.
- Свеча в ярком помещении кажется тусклой, в тёмном — яркой: яркость мы ощущаем «по контрасту».
Почему наши «очевидные» догадки часто врут
Наш мозг любит отвечать «по-простому», но природа считает по-другому. Ниже — пять бытовых ловушек, в которых интуиция обязательно сдаст экзамен.
1. Одинаковый забор — разный урожай
Допустим, вы огораживаете грядку прямоугольной формы 40 м верёвкой. Кажется, что площадь всегда будет одинаковой, но это не так. Самый большой урожай получится, если сделать участок квадратным: 10 × 10 м дадут 100 м², а 15 × 5 м — уже только 75 м². Помните: при фиксированном периметре квадрат — чемпион по площади.
Интуиция часто обманывает нас. Представьте: яблоко падает с дерева, и вы стреляете в него. Казалось бы, надо прицелиться ниже — ведь яблоко падает. Но нет: пуля и яблоко падают вниз с одинаковой скоростью, так что стреляйте прямо в цель.
Ещё пример: на теннисный турнир пришли 136 человек. Сколько нужно матчей, чтобы выявить победителя? Интуиция молчит, но ответ прост: 135 матчей. Каждый проигравший выбывает, значит, все, кроме чемпиона, должны проиграть хотя бы раз.
Почему мы ошибаемся? Интуиция — это не волшебство, а быстрый, но грубый опыт. Глаз и мозг подсказывают, что видят, но чувства могут лгать. Настоящая проверка — расчёт или эксперимент.
Как бороться с обманами чувств? Математикой. Она показывает явления, которые глаз не замечает: радиоволны, электричество, магнитные поля. Мы не чувствуем их, но пользуемся каждый день — включаем свет, звоним по телефону.
Первые шаги математики сделали ещё египтяне и вавилоняне за 3000 лет до нашей эры: считали налоги, мерили поля, строили пирамиды. Их правила были похожи на рецепты: работают, но не объясняют, почему. Это была «алхимия» математики — полезная, но ещё не наука.
Как греки придумали, что мир устроен по математическим законам
Греки первыми решили, что природа работает как точный механизм, а не как сборник чудес. Они поверили: если думать логически, можно разгадать, по каким правилам устроены вещи. Почему именно так случилось — историки не знают: документов не осталось. Одна из версий проста: вавилоняне давали разные ответы на одни и те же задачи (например, о площади круга), и греки захотели выяснить, кто прав.
Первым «доказательством» считают работы Фалеса из Милета (около 600 года до н. э.). Он будто бы логически вывел несколько геометрических теорем. Подлинных записей нет, но сам факт важен: люди начали искать не просто ответ, а убедительное объяснение.
Настоящий прорыв сделали пифагорейцы — религиозное братство, для которого число стало и богом, и строительным кирпичом мира. Они заметили: резиновый мяч и Луна разные по веществу, но оба круглые, а значит, у них одна и та же «круглая» математика. Вывод: внешний облик обманчив, а вот числовые соотношения — вечны.
Чтобы убедиться, они взяли музыку. Оказалось: если струны сделать длиной 2 к 1, звук становится ровно на октаву выше; если 3 к 2 — на квинту. Гармония оказалась арифметикой. Планеты тоже «поют»: чем дальше от Земли, тем «выше» их звук, и все эти «голоса» вместе образуют «музыку сфер». Мы её не слышим, потому что привыкли к ней с рождения.
Как древние греки догадались, что мир устроен по математическим законам
За три столетия до нашей эры греки сделали два выдающихся открытия. Во-первых, они поняли: природа работает по математическим правилам. Во-вторых, выяснили: чтобы понять устройство мира, нужно изучать числа и их соотношения. Эти идеи показались тогда странными, но позже стали основой всей науки.
Пифагорейцы первыми заметили: музыка, ремесла и даже поведение людей подчиняются числовым законам. Они не смогли доказать это на деле, но задали правильное направление мысли.
Как математика стала языком природы
Когда в V веке пала Греция, Европа на тысячу лет погрузилась в Средневековье. Церковь учила: жизнь — это подготовка к раю, поэтому изучать природу было почти грехом. Тем не менее несколько смельчаков — Роберт Гроссетест, Роджер Бэкон и другие — продолжали считать, что мир устроен разумно и математика может объяснить его устройство. Их идеи поддержали индийские и арабские учёные, принесшие в Европу новые математические знания.
К 1500 году ситуация изменилась. Европейцы вновь открыли для себя греческие труды и захотели понять устройство мира. Но возникла проблема: христианство утверждало, что всем управляет Бог, а не математические законы. Выход нашли просто — решили, что Бог создал мир по математическому плану. Получилось: изучать природу стало не грехом, а богоугодным делом. Каждое открытие воспринималось как проявление божественной мудрости.
К XVII веку интерес к реальной природе стал сильнее книжной учёности. Появились новые инструменты — телескоп и микроскоп, компас и карты. Теория Коперника перевернула представления о Вселенной. Всё это привело к научной революции, где математика стала главным ключом к пониманию мира.
Математика позволяет описывать то, что мы не видим и не чувствуем. Она работает так: сначала вводятся простые понятия — точка, линия, число. Затем человеческий разум создаёт более сложные идеи: отрицательные числа, функции, бесконечные ряды, многомерные пространства. Эти абстракции помогают находить законы, управляющие реальным миром.
Что такое математика и как она устроена
Математика — это не просто счёт и формулы. Это особый язык, который люди придумали, чтобы описывать мир. В нём есть три главные «фишки».
Первая — математика любит выдумывать странные вещи. Отрицательные числа, производные, комплексные числа — всё это сначала кажется бессмыслицей. Но если выдумка оказывается полезной (например, отрицательные числа нужны, чтобы считать долги), её начинают использовать. Сначала скептически, потом привыкают.
Вторая — математика живёт не в реальном мире, а в мире идей. Когда геометр рисует треугольник, он думает не о карандашной линии, а о «идеальном» треугольнике — таком, которого никто никогда не видел, но который объединяет всё, что угодно: треугольные куски пиццы, крыши, стрелки. То же с числами. Если купить 3 пары туфель по 20 долларов, мы не перемножаем «туфли» на «деньги». Мы выдергиваем из ситуации числа 3 и 20, перемножаем их, получаем 60 и возвращаемся к деньгам. Числа живут отдельно от туфель.
Третья — математика строится как дом. Сначала кладут «кирпичи-аксиомы» — правила, которые кажутся очевидными (например, «через две точки можно провести только одну прямую»). Потом из этих кирпичей выводят всё остальное. Некоторые слова (точка, прямая) специально не объясняют: если определять всё, придётся определять бесконечно. Аксиомы придумывают так, чтобы удобно было описывать реальность. Для отрицательных чисел нужны другие аксиомы, чем для обычных, иначе система развалится.
Как математика помогает нам понять мир
Математика работает не только с цифрами, но и с физическими знаниями. Например, законы Ньютона записаны на математическом языке. Это позволяет делать точные выводы о том, как устроен мир.
Главное преимущество математики - использование дедуктивного рассуждения. Это когда из верных посылок получаются верные выводы. Например: все люди смертны, Сократ - человек, значит Сократ смертен. Такой вывод всегда верен.
Другие способы рассуждения не дают гарантии. Если ты видел тысячу красных яблок, это не значит, что все яблоки красные. Это индуктивное рассуждение. Или если брат-близнец закончил колледж, это не значит, что и Джон закончит. Это рассуждение по аналогии.
Математика требует строгих доказательств. Даже если ты измерил сто треугольников и у всех сумма углов 180 градусов, это еще не теорема. Нужно логически доказать, что это верно для всех треугольников.
Как математика объяснила небо
Древние греки первыми заметили: за хаотичным бегом звёзд скрыт порядок, похожий на работу разума. Они решили, что небо ведёт себя не как капризное божество, а как огромный механизм, который можно описать числами.
До греков египтяне и вавилоняне знали лишь календарные приёмы: когда сеять, когда ждать разлива. Никто не искал общей картины. Греки же начали спрашивать «почему» и «как устроено всё сразу».
Первым шагом стал Милет: богатый торговый город, где люди имели досуг и свободу думать. Здесь Фалес, Анаксимандр и Анаксимен впервые объясняли мир без сказок. Они ошибались в деталях — считали звёзды ближе Солнца и не отличали планеты — но важно другое: они показали, что Вселенная подвластна человеческому разуму.
Следующий рывок сделал Пифагор. Он объединил числа и небо в одну картину, где математика становится языком космоса. Это стало фундаментом, на котором позже выстроят Коперник и Кеплер.
Как греки поняли, что Земля круглая и почему планеты ведут себя странно
За два с половиной тысячелетия до спутников и телескопов древние мудрецы поняли: наша планета — шар. Это открытие стало первым шагом к настоящей науке о небе.
Главное открытие: Земля — шар
Пифагор и его ученики в VI веке до нашей эры впервые сказали: «Земля похожа на идеальный мяч». Для них сфера была самой красивой формой, а красота, по их мнению, всегда рядом с истиной. Подтверждением служили простые наблюдения: корабли исчезают за горизонтом кормой в последнюю очередь, а во время затмений на Луне видна круглая тень Земли.
Как древние мудрецы поняли, что Земля крутится
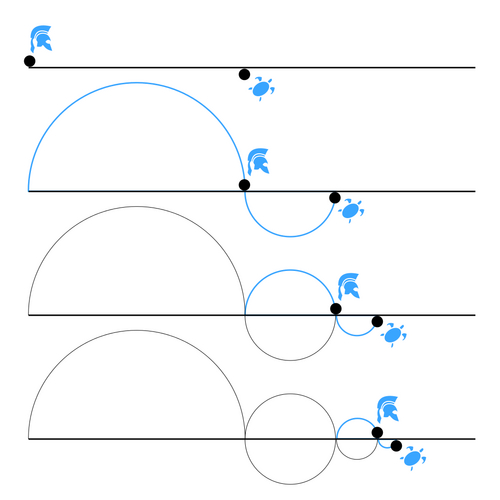
За два столетия до нашей эры люди уже догадывались, что видимое вращение звёзд — это обман. Мысль была простой: проще крутиться маленькому шару Земли, чем огромному небу. Первым это предположил пифагореец Гикет, а затем ученик Платона Гераклит объяснил, почему Солнце, Венера и Меркурий постоянно держатся вместе: малые планеты вращаются вокруг Солнца, а Солнце — вокруг Земли. Это объясняло, почему яркость планет меняется. Гераклит придумал «эпицикл» — окружность, катящуюся по другой окружности; эта идея прослужит астрономам полторы тысячи лет.
Позже, в египетской Александрии, греки получили доступ к древним вавилонским и египетским звёздным записям. При дворе Птолемеев построили «Музей» — первый государственный научный центр, снабдили учёных точными угломерами и деньгами на библиотеку. Там работали Эратосфен, Гиппарх, Птолемей и другие; их расчёты оставались лучшими до эпохи Галилея.
Самым смелым был Аристарх с острова Самос. Он решил измерить, насколько Солнце больше Луны и как далеко они находятся. Тригонометрии ещё не было, поэтому он использовал только геометрию Евклида и подборку угловых измерений. Аристарх понял, что Луна светится отражённым светом и рассчитал, что Солнце в 6–7 раз дальше Луны и примерно в 300 раз больше её по диаметру (настоящее значение ~400). Затем он выдвинул главную идею: Земля и другие планеты вращаются вокруг Солнца. Современники не приняли эту гипотезу, но она стала первым шагом к тому, чтобы человечество перестало считать себя центром мира.
Как древние учёные впервые измеряли небо и Землю
Древние греки впервые попытались узнать, насколько далеко находятся Солнце и Луна, и какие у них размеры. Аристарх Самосский использовал простую геометрию и получил примерные цифры. По современным меркам они были неточными, но главное - он показал, что такие вычисления возможны. Кроме того, Аристарх первым предположил, что Земля вращается вокруг Солнца, а не наоборот. Его идея показалась слишком смелой для современников и не получила поддержки.
Вскоре после Аристарха Эратосфен из Кирены придумал, как измерить Землю. Он заметил, что в Сиене (современный Асуан) в полдень солнце стоит прямо над головой и не оставляет тени, а в Александрии в это же время тень есть. Измерив угол тени и зная расстояние между городами, он вычислил, что длина окружности Земли составляет 250 000 стадий. Хотя его расчёты содержали ошибки, он впервые показал, что размеры нашей планеты можно вычислить.
Эти открытия стали важным шагом в развитии астрономии. Учёные научились задавать вопросы "как далеко?" и "какой размер?" и находить ответы с помощью математики. Вскоре появились более точные теории движения небесных тел. Вершиной древнегреческой астрономии стали труды Гиппарха и Птолемея, которые собрали и систематизировали все знания о небе, накопленные за предыдущие века.
Как древние «собирали» небо из кругов и почему Земля казалась центром мира
Гиппарх: «набор кругов» вместо кристального небосвода
Старый рисунок Евдокса — Земля в центре, всё вращается вокруг неё большими прозрачными сферами — не проходил проверку наблюдениями. Гиппарх заменил сферы на цепочки обычных колёс.
Представьте велосипед: маленькое колесо (планета) крутится на ободе большого колеса, а большое колесо катится вокруг Земли. Подобрав размеры и скорости, он повторил видимый путь Луны, Солнца и пяти планет с точностью до нескольких часов.
Иногда приходилось ставить три-четыре «велосипеда» друг на друге, а центр самого большого колеса сдвигать в сторону от Земли. Так появились два приёма: эпицикл (колесо на колесе) и эксцентрик (колесо с офсетным центром).
Птолемей строил небесную механику как точный конструктор: всё должно было вращаться ровными кругами.
Сначала он взял чужое и подправил. За Солнцем он усадил центр орбиты рядом с Землёй, а не на саму Землю: так проще и точнее. Луну он оставил в старой схеме «колесо на колесе», но добавил хитрое третье движение, чтобы она в нужный момент «подъезжала» к нам. Это спасало положение по долготе, но требовало, чтобы Луна раз в месяц сильно приближалась и удалялась; на глаз этого не замечали, и Птолемей закрыл глаза тоже.
Расстояния он считал по-простому: сравнил расчёт с собственными наблюдениями и выдал 30 радиусов Земли до Луны. До Солнца промахнулся в десять раз, но 1400 лет никто не проверял.
Звёзды он пересчитал, разбил на «блеск-разряды» от 1 до 6 и решил, что всё дальше – значит крупнее.
Главный трюк – планеты. Чтобы объяснить их «замедления» и «движения назад», Птолемей придумал эквант – воображаемую точку, относительно которой вращение остаётся ровным. Земля не в центре, и не в центре центра – но зато цифры сходятся. Для Меркурия пришлось добавить ещё одно маленькое колесо. Внутренние планеты (Меркурий, Венера) крутятся за год, внешние – по-своему, но тоже по таблице.
Как мы пришли к выводу, что Земля вращается вокруг Солнца
Почему это важно для психологии
Мы привыкли доверять своим глазам: солнце "встаёт" и "садится", а земля кажется неподвижной. Однако именно математика заставила человечество признать: наш опыт обманывает нас. Это открытие стало первым крупным случаем, когда человек предпочёл абстрактные расчёты собственным ощущениям.
За 1400 лет до Коперника Птолемей создал сложную систему вращающихся сфер, которая объясняла движение планет с точностью до минут. Он прекрасно понимал: это всего лишь удобная математическая модель, а не картина реального мира. Но христианский мир принял его расчёты за истину в последней инстанции.
Как Коперник упростил небо и почему это взбесило всех
К середине XVI века астрономия задыхалась от собственной громоздкости. Чтобы объяснить, почему планеты «бегают» по небу, учёные наслоили друг на друга 77 кругов – каждый новый «эпицикл» чинил дырку в прежней схеме. Картина работала, но напоминала часы с лишними шестерёнками: точно, но невозможно запомнить.
Коперник решил, что природа не может быть такой перегруженной. Он перелистал древних греков и наткнулся на забытую идею Аристарха: а что, если Земля сама кружится вокруг Солнца? Это сразу убрало лишние детали: вместо 77 колёс осталось 34. Представьте, что вы объясняете дорогу: вместо «иди до большого дуба, потом налево к пруду, потом обратно к дубу и снова к пруду» вы просто говорите: «Иди по прямой до дома».
Простота была не только математической. Коперник верил, что Бог – не хаотичный мастер, а экономный архитектор: «лишние причины» Ему не нужны. Поэтому он оставил планетам их привычные круги (других форм тогда не знали), но посадил Солнце в центр, а Землю – на орбиту вместе с другими планетами.
Идея работала, но пугала. Лютер клеймил Коперника «спятившим астрологом», Кальвин требовал: «Разве Иисус остановил Солнце, а не Землю?» Люди чувствовали, что новая схема уменьшает их значение: человек больше не сидит в центре мироздания, а мчится на вращающемся шаре чёрти где.
Когда Коперник сказал, что Земля вращается вокруг Солнца, католическая церковь назвала это «самой грязной ересью». Учёный спокойно ответил: «Библия учит, как попасть в небо, а не как оно движется». Его система упростила расчёты, но всё ещё плохо совпадала с небом.
Пятьдесят лет спустя появился Иоганн Кеплер — бедный, хилый, вечно преследуемый немец. Он верил, что Бог создал мир по простому и красивому математическому плану, и решил найти этот план в наблюдениях Тихо Браге. Годами перебирал круги, треугольники и кубы, пока не понял: теория должна подстраиваться под факты, а не наоборот. Именно это упорство помогло ему довести идею Коперника до совершенства.
Как Кеплер нашёл простые законы для сложных планет
Кеплер хотел красивой Вселенной. Он придумал, что расстояния между шестью планетами можно описать пятью правильными фигурами: куб, тетраэдр и другие. Красиво, но не сходилось с наблюдениями. Ученый не стал упрямиться: если факты против красоты — значит, красота неправильная.
Тогда он взял точные записи Тихо Браге и стал искать, что же на самом деле задаёт форму и скорость орбит. В итоге открыл три простых закона.
Первый закон: планета летит не по кругу, а по эллипсу. Солнце сидит в одном из двух «фокусов» этого эллипса. Представьте овал стола для бильярда: если раскатить шар так, чтобы он всё время касался бортика, одна из «горячих точек» будет Солнцем.
Второй закон: планета не едет равномерно. Когда она ближе к Солнцу, бежит быстрее; дальше — медленнее. Проведите воображаемую линию от Солнца до планеты. За один и тот же промежуток времени эта линия «вычерчивает» одинаковые «куски пирога» площади. Значит, зимой мы обгоняем Солнце чуть быстрее, чем летом.
Как Коперник и Кеплер перевернули мир
Сегодня мы спокойно учим, что Земля вращается вокруг Солнца. Но пять столетий назад эта идея казалась безумием.
Люди были уверены: Земля стоит в центре, а вокруг неё вращаются Солнце и звёзды. Церковь поддерживала эту модель, потому что она делала человека венцом творения. Небо находилось «наверху», ад — «внизу», всё было на своих местах.
Как появилась идея, что Земля вращается вокруг Солнца
Сегодня каждый школьник знает: Земля движется вокруг Солнца. Но 500 лет назад это звучало как безумие. Тогда все были уверены, что Земля стоит на месте, а Солнце вращается вокруг неё. Как же учёным удалось убедить людей в обратном?
Николай Коперник предложил гелиоцентрическую систему без видимых на то причин. У него не было новых наблюдений, не было предшественников, не было даже точных приборов. Его идея появилась «с потолка» и противоречила здравому смыслу.
Как телескоп разрушил старую картину мира
Галилей услышал о новом голландском «зрении на расстоянии» и за несколько недель сам сделал стеклянную трубу, увеличивающую в 30 раз. Венецианским сенаторам он показал, как за два часа до входа в порт можно разглядеть флаги кораблей. Но учёного интересовало не море, а небо.
Он первым направил трубу вверх. На Луне увидел горы и воронки, а не гладкий кристаллический шар. На Солнце нашёл тёмные пятна. Вокруг Юпитера обнаружил четыре «блуждающие звезды» — спутники, похожие на нашу Луну. Венера, как и предсказывал Коперник, меняла фазы: то тонкий серп, то полный круг. Млечный Путь распался на тысячи отдельных звёзд. Всё это говорило: Земля не центр, небесные тела не идеальны, в космосе много таких же миров.
Церковь почувствовала угрозу. В 1616 году учение Коперника объявили еретическим. Галилей, рискуя, написал книгу-разговор «Диалог о двух системах мира», где тихо, но убедительно показал преимущество солнечной системы. Папа Урбан VIII разрешил печатать, но потом испугался: аргументы слишком ясны. Учёного вызвали в Рим, заставили под присягой отречься от «ереси» и до 1822 год запретили книгу.
Современникам было трудно поверить: вся жизнь подсказывала, что Солнце ходит вокруг Земли. Сегодня мы знаем: обе картины можно построить на одних данных, но солнечная система проще считать. Главный урок: наука выбирает не «правду», а удобное объяснение, которое легче проверять и применять.
Если интересно про загадку эффективности математики в естественных науках смотрите пост
А здесь стихи и песня по этой теме.
Оригинальный текст книги Мориса Клайна (или перевод) можно изучить, если взять ее в городской библиотеке, купить или скачать откуда-нибудь
Пересказ изготовлен разными нейросетями из сканов страниц книги.