Я рассматриваю симметрию не как эстетическое свойство «красивых таблиц», а как встроенный механизм дисциплины: она задаёт, какие перенумерации полярностей допустимы, какие выражения считаются эквивалентными, как строится каноническая форма и где возникает вычислительное ускорение за счёт факторизации по орбитам.
1) Универсальная янтра и два слоя структуры: кадр и операция
Я фиксирую конечное множество полярностей P и бинарную операцию *: P x P -> P, которая задаёт закон отношений. Для конечного P операция полностью задаётся таблицей T[x][y] = x * y. Это и есть универсальная янтра в строгом смысле: полное задание бинарного закона.
Ключевой момент: в моём каноне нужно различать два слоя.
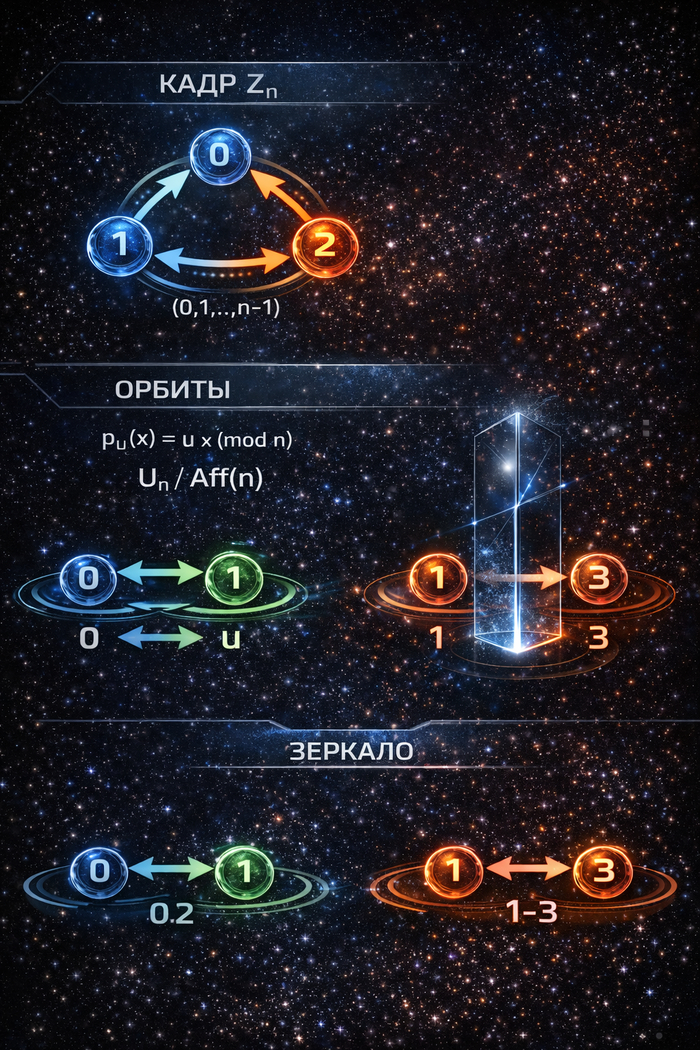
Кадр (носитель индексов). Обычно я отождествляю полярности с циклом P ≅ Z_n = {0,1,...,n-1}. Это не «сама операция», а способ организовать метки так, чтобы симметрийный каркас стал явным.
Операция (собственно янтра). Это таблица T. Она может совпадать с каноническим «плюсовым» каркасом (сложение mod n), а может быть более жёсткой (например, L4-таблица K/A/P с выделенным SUN, NEG и т.д.). Именно операция определяет реальные взаимодействия; кадр задаёт пространство перенумераций.
Если не различать эти слои, то симметрия превращается в словесную путаницу: начинают путать «перенумерацию кадра» и «автоморфизм закона».
2) Что я называю симметрией янтры
Симметрия в моей постановке — это конкретная перестановка меток, которая сохраняет закон отношений. Пусть p: P -> P — биекция. Тогда p является автоморфизмом операции, если выполнено:
p( T[x][y] ) = T[ p(x) ][ p(y) ] для всех x,y in P.
Это определение не зависит от интерпретаций и «рисунков»: оно проверяется по таблице в лоб.
Отдельно я фиксирую более широкий класс перенумераций — кадровую калибровку, которая не обязана сохранять конкретную таблицу T, но сохраняет структуру кадра Z_n. Именно здесь появляется каркас Z_n/U_n и его аффинное расширение.
3) Каркас Z_n / U_n и аффинная группа как источник дисциплины
Как только P ≅ Z_n, появляется естественная группа преобразований индексов.
U_n — множество обратимых элементов по mod n: U_n = { u : gcd(u,n)=1 }.
Автоморфизмы кадра с фиксированным нулём: x -> u*x (mod n).
Аффинные перенумерации (допускают сдвиг кадра): x -> u*x + t (mod n), где u in U_n, t in Z_n.
Эти преобразования не всегда являются автоморфизмами конкретной таблицы T, но они задают физически осмысленный малый класс кандидатов для поиска эквивалентностей и построения канона. Это принципиально: вместо перебора S_n я работаю внутри U_n или Aff(n).
4) Симметрия как факторизация вычислений: орбиты вместо полного перебора
Если проверка (валидатор) инвариантна относительно некоторой группы G, то вместо перебора P^k достаточно перебора представителей орбит:
Это не риторика про «ускорение», а конкретная процедура:
В многополярной процедуре именно проверки k=3 (тройные ограничения, мосты между операциями, замыкания) являются центрально дорогими. Поэтому орбитная факторизация превращается в основной инструмент “дешёвого ядра”.
5) Зеркало, фикс-точки и M-паритет: от симметрии к «вихрю»
Особая роль принадлежит зеркальному преобразованию m(x) = (-x) mod n.
Оно раскладывает наблюдаемые и интенсивности на два канала:
На L4 (n=4) зеркало имеет две фикс-точки, и это приводит к жёсткому ограничению: M-нечётная часть обязана зануляться на фикс-разностях и живёт только на соседних переходах. Именно здесь симметрия перестаёт быть «про переименование» и становится частью вычислимой ориентации, то есть тем, что я называю вихревым механизмом.
В трёх главах дальше я сделаю один ход: строго разведу (а) симметрии кадра и (б) автоморфизмы таблицы, затем покажу, как симметрия развивается от L2 к L4, и в конце выведу практический протокол: как из сырой таблицы/наблюдаемых получить U_n, Aff(n), орбиты, канон и тем самым дисциплинировать вычисления и остановку.
Глава 1. Симметрии как объект: кадр, операция и два уровня эквивалентности
1. Два разных смысла «симметрии», которые нельзя смешивать
Я фиксирую два уровня, которые внешне выглядят одинаково (оба — «перестановки меток»), но математически различаются принципиально.
1.1. Симметрия кадра (геометрия индексов)
Пусть P ≅ Z_n. Тогда я имею группу преобразований индексов кадра. Минимальный каркас:
U_n = { u : gcd(u,n)=1 },
действие: x -> u*x (mod n).
Расширение с кадровым сдвигом:
Это симметрия не «таблицы операции», а индексного пространства. Она отвечает на вопрос: какие перенумерации я считаю допустимыми как калибровку кадра.
1.2. Симметрия операции (автоморфизм таблицы)
Пусть задана операция *: P x P -> P и таблица T[x][y] = x*y. Тогда симметрия операции — это биекция p: P -> P, такая что:
p(T[x][y]) = T[p(x)][p(y)] для всех x,y.
Я обозначаю группу всех таких p как Aut(T).
Aff(n) задаётся структурой кадра и существует до того, как я выберу конкретную T.
Aut(T) вычисляется по таблице и может быть тривиальной даже при богатом Aff(n).
Это различие является основой дисциплины: иначе легко «доказывать» что угодно, переименовывая кадры, не фиксируя, что именно сохраняется.
2. Канонизация: зачем мне нужно различать U_n и сдвиги t
Я ввожу два класса перенумераций именно потому, что они имеют разные статусы:
Это различие немедленно проявляется как запрет «скрытого join» в рассуждении:
Если я допускаю t, я обязан явно вести кадр. Если я фиксирую ноль/якорь (например, выделенный элемент вроде SUN или ZERO), то я запрещаю t и оставляю только U_n (или стабилизатор).
Таким образом, разделение u/t — не удобство, а часть логики остановки: непроявленный сдвиг кадра должен считаться ошибкой.
3. Симметрия как факторизация перебора: орбиты и представители
Я фиксирую общий механизм:
Пусть есть выражение/проверка k-местного вида: V(x1,...,xk).
Если для всех p in G выполняется инвариантность: V(p(x1),...,p(xk)) = V(x1,...,xk), то проверку достаточно проводить по представителям орбит:
Это даёт вычислительную экономию, но важнее — даёт канон, потому что каждый класс эквивалентных конфигураций имеет представитель.
В многополярной архитектуре наиболее дорогой слой почти всегда k=3 (тройные тождества, мосты, замыкание). Поэтому симметрийная факторизация концентрируется именно там.
4. Две основные симметрийные структуры: вращение и зеркало
Поскольку P ≅ Z_n, на кадре существуют два концепта, которые затем «встраиваются» в операцию и наблюдаемые.
4.1. Вращения (циклические сдвиги)
Если кадр допускает калибровку, эти преобразования допустимы как изоморфизмы кадра. Но если выделен якорь (нулевой элемент, SUN и т.п.), то они обычно запрещаются.
4.2. Зеркало
Оно порождает разложение на два канала (even/odd). Это принципиально для L4, потому что число фикс-точек зеркала зависит от n и меняет структуру возможных инвариантов.
5. Минимальные примеры: что случается с симметриями на L2/L3/L4 (в виде тезисов)
Я фиксирую свойства, которые я затем строго разворачиваю в следующих главах.
L2 (n=2): зеркало вырождается (m(x)=x), поэтому ориентационный (odd) канал невозможен; симметрия кадра почти полностью сводится к переименованию двух меток и исчезает при фиксации якоря.
L3 (n=3): появляется нетривиальная инверсия x -> -x, есть одна фикс-точка (0) и обменная пара (1↔2); возникает минимальная ориентация.
L4 (n=4): зеркало имеет две фикс-точки (0 и 2) и обменную пару (1↔3); возникает жёсткая локализация odd-канала на соседних переходах, а even-структура распадается на три класса разностей.
Эти тезисы не про «картинки», а про структуру групп и фикс-точек зеркала, то есть про неизбежную арифметику Z_n.
Итог главы 1 (как строгая опорная рамка)
Есть два уровня симметрии: Aff(n) как симметрия кадра и Aut(T) как симметрия операции.
Разделение u и t — это дисциплина кадра и запрет скрытого смешения рамок.
Симметрия даёт не только классификацию, но и вычислительную схему: орбиты Z_n^k / G вместо полного перебора.
На кадре ключевые преобразования — сдвиг и зеркало; роль зеркала определяется числом фикс-точек, а это меняется на L2/L3/L4.
Глава 2. Развитие симметрий по уровням L2 → L3 → L4: группы, фикс-точки и канонические классы
1. Общая схема: что именно «развивается» при переходе L2→L3→L4
Я рассматриваю развитие симметрий не как наращивание словаря, а как изменение трёх строго определённых объектов:
Носитель кадра: P ≅ Z_n с n=2,3,4.
Группа кадра: U_n и её аффинное расширение Aff(n)=U_n⋉Z_n.
Зеркало и его фикс-точки: m(x)=-x (mod n).
В этой рамке «закономерность» означает конкретные формулы для:
2. L2: симметрия вырождается в переименование и не несёт ориентации
2.1. Кадр и группы
U_2 = {1} (единственная единица по mod 2).
Aff(2) = U_2 ⋉ Z_2 имеет размер |Aff(2)| = 2.
То есть кадр допускает только тождественное умножение и возможный сдвиг t (который в Z_2 совпадает с обменом двух меток).
2.2. Зеркало
m(x) = -x (mod 2) даёт: m(0)=0, m(1)=1.
Зеркало совпадает с тождеством, то есть вырождено.
нет различия «вперёд/назад»,
нет ненулевого M-нечётного (ориентационного) канала,
любые “вихревые” эффекты на L2 могут быть только внешней интерпретацией, но не структурным фактом кадра.
2.3. Орбиты разностей
Разности delta=(y-x) mod 2 имеют два класса: 0 и 1. Это и есть вся симметрийная классификация связи/наблюдаемых на L2.
3. L3: минимальная невыражденная ориентация появляется как следствие U_3
3.1. Кадр и группы
U_3 = {1,2} (две единицы по mod 3), размер |U_3|=2.
Aff(3) имеет размер: |Aff(3)| = |U_3| * |Z_3| = 2*3 = 6.
Важно: это уже не «почти тривиально», а полноценный симметрийный каркас, дающий факторизацию.
3.2. Зеркало и фикс-точки
Здесь есть ровно одна фикс-точка: {0}, и одна обменная пара {1,2}.
Это первый уровень, где ориентация появляется неизбежно: существует преобразование x -> -x, которое не тождественно.
3.3. Орбиты разностей и канонические классы
delta=0,
delta=1,
delta=2=-1 (mod 3).
Под действием зеркала delta -> -delta получаю:
Следовательно, есть два even-класса: {0} и {1,2}, и один odd-канал, который меняет знак на паре {1,2}.
Эта структура и есть минимальный «вихрь» L3: ориентация существует, но не имеет внутренних фикс-разностей кроме нуля, поэтому она ещё не локализована так жёстко, как на L4.
4. L4: качественный скачок — две фикс-точки зеркала и новый класс «противоположности»
4.1. Кадр и группы
U_4 = {1,3} (две единицы по mod 4), размер |U_4|=2.
Aff(4) имеет размер: |Aff(4)| = |U_4| * |Z_4| = 2*4 = 8.
Формально размеры U_n на L3 и L4 одинаковы (оба раза 2), но геометрия фикс-точек зеркала различна, и именно она меняет классификацию.
4.2. Зеркало и фикс-точки
m(0)=0,
m(2)=2,
m(1)=3,
m(3)=1.
Фикс-точки: {0,2} — их две.
Это принципиальный факт: на L4 появляется «ось» (две неподвижные точки), которая делит кадр на фиксированную часть и обменную пару.
4.3. Орбиты разностей и канонические классы
Разности: delta in {0,1,2,3}.
Отсюда канонические классы:
{0} (самосвязь),
{2} (противоположность),
{1,3} (соседство).
И это уже не то же самое, что на L3: появляется отдельный класс delta=2, который не смешивается ни с 0, ни с ±1.
4.4. Жёсткая локализация odd-канала
Для odd-компоненты выполняется антисимметрия: k_odd(-delta) = -k_odd(delta).
Но на фикс-разностях delta=-delta (то есть на 0 и 2) это даёт: k_odd(delta)=0.
Следовательно, на L4 odd-канал может жить только на delta=1 и delta=3, и обязательно с противоположными знаками.
Это и есть строгая причина того, что «вихрь L4» вычислительно дешёв: он параметризуется одной степенью свободы и не размазывается по всему кадру.
5. Закономерность в одном выражении: фикс-точки зеркала задают архитектуру симметрий
Я могу сформулировать ключевую закономерность так:
На Z_n зеркало m(x)=-x имеет столько фикс-точек, сколько решений у уравнения 2x=0 (mod n).
Для n=2 решений 2 (оба элемента), но зеркало тривиально и не создаёт ориентации.
Для n=3 решений 1 (только 0), и появляется минимальная ориентация.
Для n=4 решений 2 (0 и 2), и ориентация становится локализованной: odd зануляется на фикс-классах и живёт только на соседях.
Эта арифметика является внутренней причиной различий L2/L3/L4: симметрия «развивается» как следствие уравнения 2x=0 на кадре, а не как произвольное расширение таблицы.
Итог главы 2
L2: кадр почти не несёт симметрий, зеркало вырождено, ориентационного канала нет; остаются только два класса разностей {0} и {1}.
L3: появляется нетривиальная инверсия и одна фикс-точка зеркала; возникают два even-класса {0} и {1,2} и минимальный odd-канал на паре {1,2}.
L4: появляется второй фиксированный класс {2} и обменная пара {1,3}; odd-канал вынужденно зануляется на {0,2} и живёт только на {1,3}.
Эта структура заранее задаёт канонизацию, факторизацию перебора и разделение “фона” и “вихря” в любых наблюдаемых и интенсивностях, построенных на L3/L4.
Глава 3. Протокол симметрий: как из янтры и сырья получить U_n/Aff(n), автоморфизмы, канон и ускорение
1. Цель: симметрия как рабочий механизм, а не как рассуждение “про группы”
Эта глава фиксирует итоговую процедуру: я превращаю симметрию в исполнимый протокол, который делает три вещи одновременно:
Достаёт каркас симметрий из определения кадра Z_n (U_n, Aff(n), зеркало, фикс-точки).
Сканирует реальную янтру (таблицу операции) и находит Aut(T) внутри осмысленного малого класса.
Строит каноническую форму для таблиц и наблюдаемых и тем самым факторизует перебор.
Я не перехожу к “перебору S_n”, потому что это ломает сам смысл дисциплины: симметрия здесь — это способ не терять контроль кадра и не платить квадратичной/кубической сложностью там, где структура уже дала редукцию.
2. Протокол для таблицы операции: SYM_SCAN_RAW_V1 в жёсткой математической форме
2.1. Вход
Дана таблица операции T: Z_n x Z_n -> Z_n, то есть T[x][y] — значение x*y.
2.2. Класс кандидатов перенумераций
Я фиксирую класс перенумераций (в зависимости от дисциплины кадра):
режим U_n (фиксирован ноль/якорь): p_u(x)=u*x (mod n),
режим Aff(n) (допускаю калибровку кадра): p_{u,t}(x)=u*x+t (mod n).
Это принципиально: я перехожу от гигантского S_n к малому Aff(n).
2.3. Тест автоморфизма (строгое условие)
Для каждого кандидата p проверяется: p( T[x][y] ) = T[ p(x) ][ p(y) ] для всех x,y.
Кандидаты, прошедшие тест, образуют группу автоморфизмов таблицы: Aut_G(T) = { p in G : p(T)=T }, где G — выбранный класс (U_n или Aff(n)).
если Aut_G(T) тривиальна, это не «плохо», это означает жёсткость таблицы при заданных якорях;
если Aut_G(T) нетривиальна, это сразу даёт факторизацию: все эквивалентные состояния/тройки можно сводить к представителям орбит.
2.4. Каноническая форма таблицы
Я определяю действие p на таблицу как перенумерацию индексов и значений: (T^p)[i][j] = p( T[ p^{-1}(i) ][ p^{-1}(j) ] ).
Тогда канон: Canon(T) = min_{p in G} flatten(T^p) в лексикографическом порядке на списке длины n^2.
Это и есть строгая “канонизация по симметриям”: один представитель на орбиту.
3. Протокол для наблюдаемых/рядов: инвариантность и M-паритет
3.1. Вход
Дана наблюдаемая на кадре:
O: Z_n -> R (вектор),
или O: Z_n x Z_n -> R (матрица),
или O: Z_n^k -> R (k-местная метрика, чаще k=3).
3.2. Проверка инвариантности/ковариантности
инвариантность: O(p(x)) ≈ O(x) (или аналогично для многомерных O),
антиинвариантность (sign-режим): O(p(x)) ≈ -O(x),
где ≈ — равенство с допуском.
множество симметрий, сохраняющих канал,
множество симметрий, меняющих знак.
3.3. Зеркало и разложение even/odd
Задаю зеркало: m(x) = -x (mod n).
Ключевая закономерность: если x — фикс-точка зеркала (m(x)=x), то для M-нечётного канала обязательно O(x) ≈ 0.
На L4 это даёт жёсткие нули на фиксированных классах и тем самым фиксирует, где вихрь может жить, а где не имеет права проявляться.
4. Симметрия как ускорение: орбиты Z_n^k/G и оценка сжатия
Я фиксирую центральную инженерную лемму:
Лемма 4 (орбитная факторизация). Если валидатор/метрика V инвариантен относительно G, то вместо перебора всех Z_n^k достаточно перебора представителей орбит Z_n^k / G.
Именно k=3 является критическим уровнем стоимости. Поэтому я получаю ускорение в дорогих проверках не за счёт эвристик, а за счёт уменьшения количества случаев.
Практические следствия для L3/L4 в симметрийном режиме Aff(n):
L3: вместо 3^3 = 27 троек я перебираю лишь представителей орбит (это число мало и стабильно).
L4: вместо 4^3 = 64 троек я перебираю ещё меньше представителей, а odd-канал дополнительно локализован.
Смысл здесь не только в скорости: орбиты дают канон, а канон даёт дисциплину и воспроизводимость.
5. Итоговая «трёхслойная» классификация симметрий янтры
Вся симметрийная логика, если её записать кратко и окончательно, распадается на три слоя:
Кадровая симметрия (структура индексов): Z_n задаёт U_n, Aff(n) и зеркало m(x)=-x.
Операционная симметрия (автоморфизмы таблицы): Aut(T) определяется строгим равенством p(T[x][y])=T[p(x)][p(y)].
Симметрия наблюдаемых (каналы и паритет): инвариантность/антиинвариантность по G и M-паритет по зеркалу.
Это и есть механизм, который «угадывает симметрии» непосредственно из определения кадра и затем дисциплинирует вычисления по реальной таблице и сырью.
Итоги
Симметрия универсальной янтры — это не просто красивое оформление и не просто способ рассказать историю. Это рабочий инструмент, который выполняет четыре конкретные задачи:
Определяет, что считать эквивалентным. Через математические операции U_n/Aff(n) симметрия задаёт чёткие правила: какие варианты считаются «одинаковыми» с точки зрения структуры.
Создаёт единый стандарт представления. Она указывает, как должна выглядеть «правильная» (каноническая) форма таблицы и наблюдаемых величин — это позволяет всем работать с одним и тем же шаблоном.
Ускоряет вычисления. Вместо того чтобы проверять все возможные варианты (полный перебор), симметрия позволяет работать с группами эквивалентных случаев — так называемыми «орбитами». Это экономит время и ресурсы.
Вводит строгие ограничения. Симметрия запрещает скрытые изменения (сдвиги t), если в системе есть фиксированные точки отсчёта («якоря»). Это делает работу предсказуемой и контролируемой.
Зачем это нужно? Допустим, мы хотим построить вычисления по принципам LLM, но с учётом особенностей вихревых структур L3/L4. В этом случае симметрия даёт нам то, чего не может обеспечить обычная статистическая модель:
право на остановку — чёткие критерии, когда можно завершить расчёт;
протокол — пошаговую инструкцию, как проводить вычисления;
канон — единый формат представления результатов;
локализацию конфликтов — возможность находить и исправлять ошибки в конкретных местах, а не во всей системе.
При этом вся работа выполняется с гораздо меньшими вычислительными затратами.
Как повторить
Текст статьи подготовлен с использованием ChatGPT. Однако он опирается на архив проекта, в котором зафиксированы структура многополярности (единый граф), протокол запуска и контрольные процедуры (гейты), обеспечивающие воспроизводимость и логическую дисциплину.
Скачайте архив MP_YANTRA_CORE_iter064.zip, загрузите его в первое сообщение чата ChatGPT и напишите:
«Следуй инструкциям в файле DOCS/00_NEW_CHAT_PROTOCOL.md из загруженного архива».
Дальше задавайте любые вопросы по многополярности (в пределах двухполярности L2, трехполярности L3, четырехполярности L4).
Я отвечаю на все вопросы! На любой вопрос получите разумный ответ. Даже если Вам показалось, что это бред — просто задайте вопрос! Ответ будет четкий и по существу!