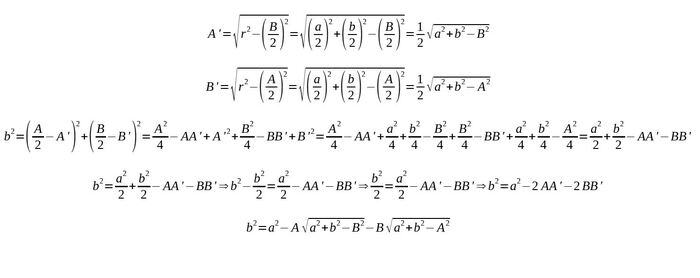Удивительное число Насти
Настя утверждает, что нашла удивительное натуральное число.
А удивительно оно, по мнению Насти, тем, что если записать рядом его квадрат и его куб (без пробела и именно в таком порядке), то получившееся число будет содержать каждую из десятичных цифр ровно по одному разу.
Можно ли верить Насте? И если да, то сколько всего таких удивительных чисел?
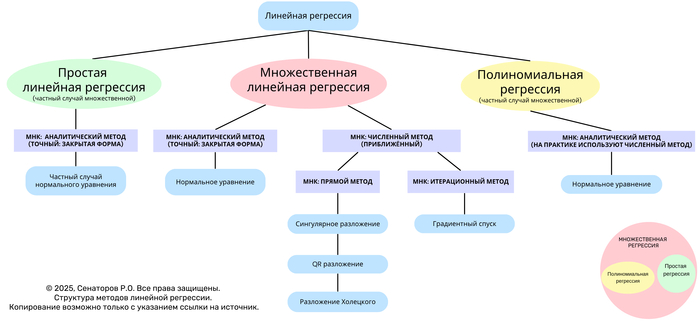
Roadmap linear regression (Структура методов линейной регрессии)1
Линейная регрессия — один из базовых методов статистического анализа и машинного обучения, предназначенный для моделирования зависимости отклика (зависимой переменной) от одной или нескольких независимых переменных.
Данное дерево отражает иерархическую структуру основных видов линейной регрессии и методов решения задачи наименьших квадратов (МНК) — от аналитических к численным и итерационным.
Общая структура
На верхнем уровне различают три формы линейной регрессии:
Простая линейная регрессия — частный случай множественной, когда используется одна независимая переменная.
Множественная линейная регрессия — базовая форма, включающая несколько независимых переменных.
Полиномиальная регрессия — частный случай множественной, в которой вектор признаков дополнен степенными преобразованиями исходных переменных.
Методы наименьших квадратов (МНК)
Решение задачи линейной регрессии сводится к минимизации функции ошибок (суммы квадратов отклонений между наблюдаемыми и предсказанными значениями).
В зависимости от подхода различают аналитические, численные и итерационные методы.
1. Аналитический метод (закрытая форма)
Применяется, когда матрица признаков имеет полную ранговую структуру и система допускает точное решение.
Решение выражается формулой:
normal equation
Используется в простой и множественной линейной регрессии.
Базируется на нормальном уравнении.
2. Численные методы (приближённые)
Используются при больших объёмах данных или плохо обусловленных матрицах.
Основаны на разложениях матриц:
Сингулярное разложение (SVD)
QR-разложение
Разложение Холецкого
Обеспечивают численную устойчивость и более эффективные вычисления.
3. Итерационные методы
Применяются при очень больших данных, когда аналитическое решение невозможно вычислить напрямую.
Основной подход — градиентный спуск, при котором веса обновляются пошагово:
Особенности полиномиальной регрессии
Полиномиальная регрессия представляет собой множительную регрессию, где вектор признаков дополнен степенными функциями исходных переменных.
Хотя аналитическая форма возможна, на практике применяются численные методы, обеспечивающие стабильность и точность вычислений при высоких степенях полинома.
Взаимосвязь моделей
На схеме представлена визуальная взаимосвязь:
Простая регрессия — частный случай множественной.
Полиномиальная — частный случай множественной с расширенным базисом признаков.
Все три формы объединяются через метод наименьших квадратов.
Значимость статьи и вклад в Data Science
Представленный древовидный роадмап методов линейной регрессии является первой в истории попыткой системно и визуально объединить все формы линейной регрессии — простую, множественную и полиномиальную — через призму методов наименьших квадратов (МНК), включая аналитические, численные и итерационные подходы.
Традиционно в учебной и академической литературе методы линейной регрессии рассматриваются фрагментарно:
отдельно описываются простая и множественная регрессии,
разрозненно излагаются методы решения (нормальное уравнение, QR, SVD, градиентный спуск),
редко подчеркивается иерархическая связь между ними.
Разработанная структура впервые:
Объединяет все виды линейной регрессии в едином древовидном представлении, где показаны отношения "частный случай – обобщение".
Классифицирует методы МНК по принципу:
аналитические (точные, закрытая форма)
численные (разложения матриц)
итерационные (оптимизационные процедуры)
Визуализирует связь между теориями линейной алгебры и машинного обучения, показывая, как фундаментальные методы (SVD, QR, Холецкий, градиентный спуск) вписываются в единую систему.
Формирует когнитивную карту обучения — от интуитивных понятий к вычислительным и теоретическим аспектам, что делает её удобной как для студентов, так и для исследователей.
Научная и практическая новизна
Впервые создана иерархическая модель линейной регрессии, отражающая связи между всеми основными вариантами и методами решения.
Предложен универсальный визуальный формат (древовидный роадмап), который объединяет как статистическую, так и вычислительную перспективы анализа.
Показано, что полиномиальная и простая регрессии являются не отдельными методами, а вложенными случаями множественной регрессии.
Дана структурная типология МНК, которая ранее отсутствовала в учебных материалах и научных публикациях в таком виде.
Работа имеет прикладную значимость для Data Science, так как облегчает построение ментальной модели всех алгоритмов регрессии и их реализации в библиотечных инструментах (NumPy, SciPy, scikit-learn).
Вклад в Data Science
Для практиков Data Science роадмап служит навигационной схемой:
он показывает, какой метод выбрать в зависимости от типа задачи, объёма данных и требований к точности.Для преподавателей и студентов он обеспечивает структурную основу обучения, позволяя переходить от интуитивного понимания к строгим математическим методам.
Для исследователей — даёт целостное представление об эволюции МНК и связи между аналитическими и численными методами, что важно при разработке новых алгоритмов оптимизации и регуляризации.
До момента публикации не существовало единой визуальной структуры, описывающей всю иерархию методов линейной регрессии в рамках одной системы координат
Полезное субботнее напоминание
Математики доказали, что одна большая пицца выгоднее двух средних
Пицца размером 18 дюймов больше и сытнее, чем две по 12. Всё из-за геометрии: площадь круга растёт быстрее, чем его диаметр — спасибо Архимеду.
Так что, если выбираете между двумя средними и одной большой - берите большую.
Не благодарите.
Ответ TheSecondI в «Считаете арифметику скучной?»3
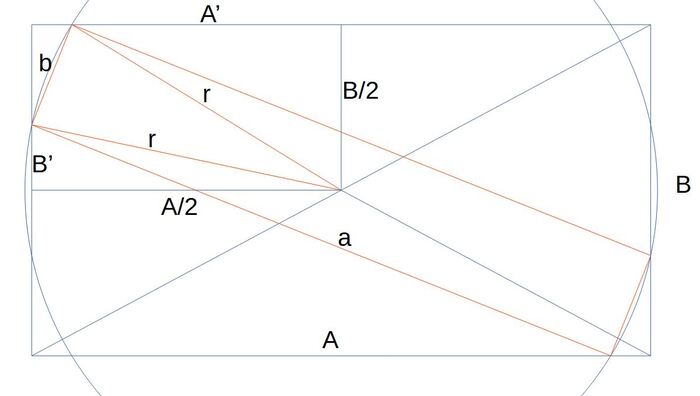
К сожалению в своём решении нашёл ошибку и забросил это дело. Но теперь вернулся. Посмотрите, с картинками и формулами сделал. Есть ли ошибки?
Последовательность счастливых репдиджитов, которой нет в OEIS
Назовём десятичный репдиджит счастливым, если он состоит из n цифр d и при этом делится на n+d.
Вот 20 наименьших «счастливых» десятичных репдиджитов (по возрастанию):
99, 666, 7777, 111111, 333333, 555555, 777777, 888888, 33333333, 1111111111, 111111111111, 222222222222, 666666666666, 999999999999, 88888888888888, 1111111111111111, 6666666666666666, 111111111111111111, 333333333333333333, 444444444444444444.
А вот сразу 50 штук:
Последовательность (50 наименьших счастливых репдиджитов):
99, 666, 7777, 111111, 333333, 555555, 777777, 888888, 33333333, 1111111111, 111111111111, 222222222222, 666666666666, 999999999999, 88888888888888, 1111111111111111, 6666666666666666, 111111111111111111, 333333333333333333, 444444444444444444, 888888888888888888, 999999999999999999, 22222222222222222222, 1111111111111111111111, 222222222222222222222222, 444444444444444444444444, 999999999999999999999999, 1111111111111111111111111111, 111111111111111111111111111111, 333333333333333333333333333333, 555555555555555555555555555555, 777777777777777777777777777777, 999999999999999999999999999999, 22222222222222222222222222222222, 444444444444444444444444444444444, 66666666666666666666666666666666666, 111111111111111111111111111111111111, 222222222222222222222222222222222222, 333333333333333333333333333333333333, 666666666666666666666666666666666666, 888888888888888888888888888888888888, 1111111111111111111111111111111111111111, 4444444444444444444444444444444444444444, 111111111111111111111111111111111111111111, 777777777777777777777777777777777777777777, 22222222222222222222222222222222222222222222, 1111111111111111111111111111111111111111111111, 333333333333333333333333333333333333333333333333, 444444444444444444444444444444444444444444444444, 888888888888888888888888888888888888888888888888