Аритмомахия (пункт 4, вещественные числа)
Рациональные числа (ℚ) научили нас искусству деления целого: 3 яблока на 4 друзей (¾), ½ метра ткани, решение уравнения 2x = 1 (x = ½). Но мир не сводится к отношениям целого.
Как измерить диагональ единичного квадрата? Как описать длину окружности диаметром 1? Как выразить мгновенную скорость или непрерывный рост?
Рациональные числа бессильны перед лицом непрерывности, так как их дискретность оставляет бездонные пропасти между точками. √2 нельзя записать дробью, π и e выпадают из сетки p/q, а уравнение x²=2 не имеет корней в ℚ.
Добро пожаловать в мир непрерывного бытия вещественных чисел (ℝ).
Примечание: ℕ, ℤ, ℚ, ℝ и ℂ— стандартные символы Юникода (exempli gratia, ℕ = U+2115), предназначенные специально для множества натуральных, целых, рациональных, вещественных и комплексных чисел соответственно. Использование данных символов исключает двусмысленность, вроде "...пусть N — натуральное число, тогда N ∈ N", что только запутает читателя.
Древний мир столкнулся с загадкой непрерывности через геометрию. Пифагорейцы (V в. до н.э.), открыв иррациональность √2, пытались скрыть это:
Гиппас из Метапонта был изгнан за доказательство, что диагональ квадрата несоизмерима со стороной
— Ямвлих, "О пифагорейской жизни".
Это было связано с тем, что пифагорейцы обожествляли целые числа и их отношения. Их доктрина гласила:
Всё сущее есть число,
подразумевая, что любую величину (длину, площадь, гармонию) можно выразить дробью p/q. Открытие, разрушившее эту веру, возникло при изучении диагонали квадрата со стороной 1. оказалось, что никакая дробь не укладывается точно ни в диагональ, ни в сторону. Гиппас предположил, что 2=pq2=qp (дробь несократима). Тогда:
p² = 2q²
Отсюда:
p² чётно → p чётно → p = 2k → 4k² = 2q² → q² = 2k² → q чётно.
Дробь оказалась сократимой. Пифагорейцы назвали такие числа "алогон" (невыразимое).
Античный ответ дал Евдокс Книдский (IV в. до н.э.). В "Началах" Евклида (Книга V) он создал теорию пропорций для величин любой природы:
Говорят, что величины находятся в том же отношении a:b = c:d, если равны их кратные: m·a > n·b ⇔ m·c > n·d.
Средневековый Восток приблизился к идее предела. Ал-Каши (XV в.) в "Ключе арифметики" вычислял π с 16 знаками, разбивая окружность на 805 306 368 частей.
Длина полуокружности диаметра 1 есть 3;1415926535897932...
Для этого он вписал в окружность правильный многоугольник с 805 306 368805306368 сторонами, последовательно удваивая число сторон и вычисляя длину каждой новой стороны через предыдущую:
a₂ₙ = √(2 - √(4 - aₙ²)), где aₙ — сторона n-угольника.
Результат записал как: π ≈ 3;8 29 44 0 47 25 53 7 25 (в шестидесятеричных долях). Стоит отметить, что его метод предвосхитил интегральное исчисление.
Перелом наступил в XVII веке. Бонавентура Кавальери в "Геометрии неделимых" (1635) представлял площади как суммы бесконечно тонких линий:
Фигура — ткань из всех своих сечений, как ткань — из нитей.
Exempli gratia: необходимо вычислить площадь круга радиуса R. Для этого круг разрезается на n бесконечно тонких колец толщиной dx. Площадь кольца на расстоянии x от центра:
dA = 2π√(R² - x²) dx.
Суммируя:
A = ∫₋ᵣᴿ 2π√(R² - x²) dx = πR².
Ньютон в "Методе флюксий" (1671) пошел дальше:
Величины исчезающе малые суть пределы отношений приращений.
Флюэнта (x) — изменяющаяся величина (например, координата). Флюксия (ẋ) — скорость изменения (производная).
ẋ = lim_{h→0} [x(t+h) - x(t)] / h.
XIX век дал ℝ аксиоматический фундамент. Рихард Дедекинд в "Непрерывность и иррациональные числа" (1872) ввел сечения:
Если все рациональные числа разбиты на два класса так, что каждый элемент первого класса меньше любого элемента второго — это сечение определяет вещественное число.
Его современник, Георг Кантор, построил ℝ через фундаментальные последовательности:
Число есть класс эквивалентности последовательностей Коши в ℚ.
А Карл Вейерштрасс, в свою очередь, завершил процесс:
Вещественные числа суть полное архимедово упорядоченное поле.
До XX века вещественные числа не имели универсального символа. В трудах Коши (1821) они назывались quantités, у Вейерштрасса (1860-е) reelle Zahlen, у Гильберта (1899) kontinuum. Перелом наступил в 1939 году, когда группа французских математиков под псевдонимом Николя Бурбаки выпустила IV том "Éléments de mathématique".
Обозначим через ℝ совершенное тело, порожденное топологией прямой
— Элементы математики, Т. IV.
ℝ от "réel, "вещественный", в противовес ℂ, "complexe".
В лекции "О бесконечном", в 1925 году, Давид Гильберт, защищая теорию множеств Кантора от критики математиков0интуицинистов, вроде Л. Э. Я. Брауэра, сказал:
Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können.
- Gesammelte Abhandlungen, Bd. 3, S. 170
Вещественные числа (ℝ) строятся как пополнение рациональных чисел, заполняющее принципиальные пробелы в числовой прямой. Основными конструкциями являются:
Сечения Дедекинда (1872):
ℝ = { разбиения ℚ на два непустых класса (A, B) | ∀a∈A, ∀b∈B: a < b }.
Пример:
√2 = { a∈ℚ | a² < 2 } ∪ { b∈ℚ | b² > 2 }.
Фундаментальные последовательности Коши (Кантор, 1872):
ℝ = классы эквивалентности последовательностей {xₙ}⊂ℚ, где
∀ε > 0 ∃N: ∀m,n > N |xₘ - xₙ| < ε
с эквивалентностью: {xₙ} ∼ {yₙ} ⇔ lim_{n→∞} |xₙ - yₙ| = 0.
Примеры:
√2: {1; 1.4; 1.41; 1.414; ...}
π: {3; 3.14; 3.141; 3.1415; ...}
e: {(1 + 1/n)^n}_{n=1}^{∞}
Операции
Сложение:
[{xₙ}] + [{yₙ}] = [{xₙ + yₙ}]
Пример:
√2 + 1 = [{1+1; 1.4+1; 1.41+1; ...}] = {2; 2.4; 2.41; ...}
Умножение:
[{xₙ}] · [{yₙ}] = [{xₙ · yₙ}]
Пример:
√2 · √2 = [{1·1; 1.4·1.4; 1.41·1.41; ...}] = {1; 1.96; 1.9881; ...} → 2
Аксиомы алгебраической структуры (наследуются от ℚ):
Сложение — абелева группа:
Ассоциативность: (a+b)+c = a+(b+c)
Нулевой элемент: a+0 = a
Противоположный элемент: a + (-a) = 0
Умножение (ℝ{0}) — абелева группа:
Обратный элемент: a · a^{-1} = 1
Дистрибутивность: a · (b+c) = a·b + a·c
Аксиомы порядка:
Трихотомия: ∀a,b ∈ ℝ: (a < b) ∨ (a = b) ∨ (a > b)
Монотонность:
a < b ⇒ a + c < b + c
a < b, c > 0 ⇒ a·c < b·c
Аксиома полноты (ключевое отличие!):
Всякое непустое ограниченное сверху множество A ⊂ ℝ имеет sup A.
Пример: A = {x ∈ ℚ | x² < 2} имеет sup A = √2 ∉ ℚ.
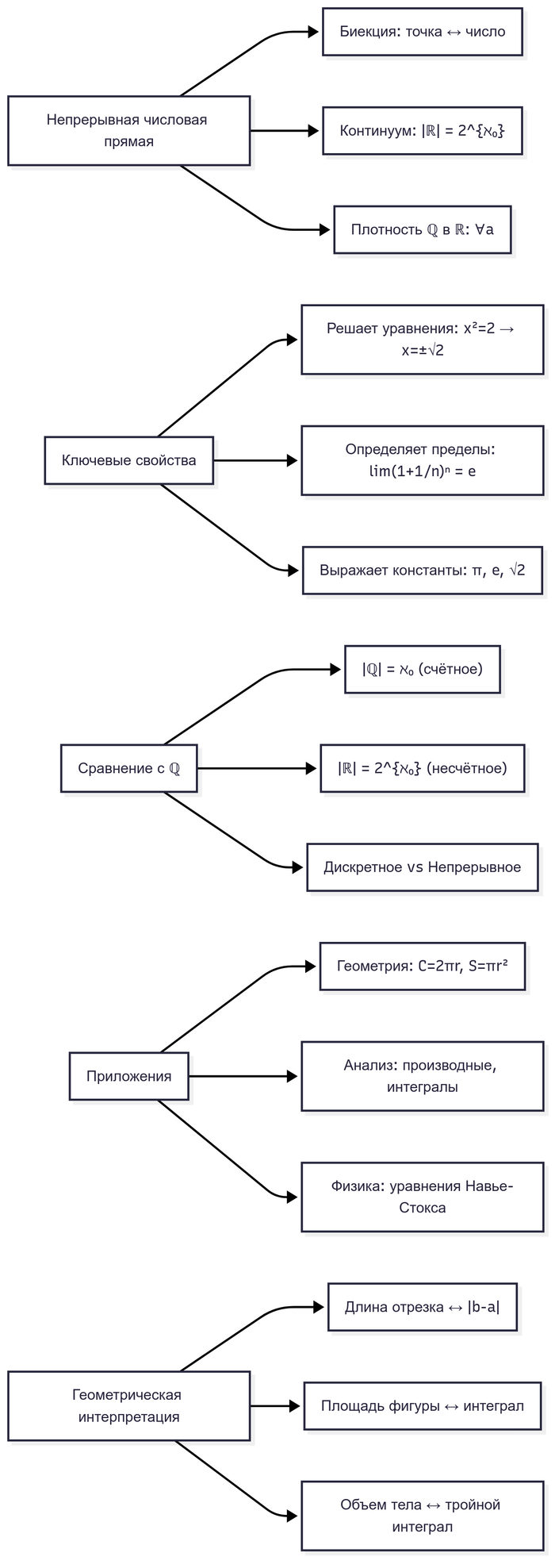
Геометрический смысл
Непрерывная числовая прямая: каждой точке прямой взаимно однозначно соответствует вещественное число.
Континуум: мощность |ℝ| = 2^{ℵ_0} (несчётное множество), тогда как |ℚ| = ℵ_0 (счётное множество).
Вещественные числа (ℝ) связаны с рациональными (ℚ) через вложение (f: ℚ → ℝ, f(r) = [{r, r, r, ...}]) и плотность (∀a,b ∈ ℝ (a < b) ∃r ∈ ℚ: a < r < b)
Пример: между √2 ≈ 1.414 и 1.415: 1.4145 = 2829/2000.
Расширение до вещественных чисел решило проблемы ℚ с корнями уравнений и пределами, однако это не устраняет принципиально новые вызовы:
Во-первых, почти все вещественные числа не имеют алгоритмического описания: вычислимые числа (задаваемые программой) образуют счётное множество (|выч. чисел| = |ℕ| = ℵ₀) и мощность ℝ — континуум (|ℝ| = 2^{ℵ₀}) приводит к тому, что ⇒ >99.9% чисел в ℝ не выразимы формулами, не вычислимы на практике.
Пример:
Константа Ω (Хайтина):
Ω = ∑_{p останавливается} 2^{-|p|} определена, но её биты невозможно вычислить.
Во-вторых, невозможно создать корректную универсальную запись из-за неединственности (0.999... = 1.000... (дуализм в десятичной системе)), неполноты (в любой системе счисления большинство чисел требуют бесконечных дробей: 1/3 = 0.333..._{10} = 0.010101..._2) и парадокса: число π нельзя точно записать даже в системе счисления с иррациональным основанием.
В-третьих, для чисел, заданных алгоритмически,
a = \sum_{n=1}^{\infty} \frac{(-1)^n}{n!}, \quad b = \int_0^1 e^{-x^2} dx
не существует алгоритма, проверяющего a = b, поэтому открыт вопрос об иррациональности e + π (хотя доказано, что min(e+π, e·π) иррационально).
В-четвёртых, любая аксиоматизация ℝ (напр., теория вещественно замкнутых полей) неполна, так как существуют утверждения вида:
∀x ∈ ℝ \ (P(x) = 0 ⇒ Q(x) > 0)
которые недоказуемы и неопровержимы.
Пример: гипотеза Континуума (2^{ℵ₀} = \aleph_1) независима от ZFC.
В-пятых, простые действия становятся неразрешимыми:
Сравнение: Для вычислимых a, b задача a < b не имеет общего алгоритма.
Интегрирование: Проверка \int_a^b f(x) dx = 0 неразрешима для элементарных f(x) (теорема Ричардсона, 1968).
Контрпример: \int_0^1 \frac{\sin x}{x} dx = \text{Si}(1) — значение неизвестно.
В-шестых, при аксиоме выбора существуют неизмеримые множества, exempli gratia построение Витали: разбиение [0,1] на сдвиги по ℚ ∩ [-1,1]. Невозможно определить длину таких множеств, что ставит под сомнение применимость ℝ в физике.
В-седьмых, большинство чисел в ℝ трансцендентны. Известно примерно 50 таких чисел (e.g., e, π, e^\pi). Нет алгоритма проверки трансцендентности для выражений:
\alpha = \pi + e, \quad \beta = \pi^{\sqrt{2}}. Неизвестно, является ли \zeta(5) = \sum_{n=1}^{\infty} \frac{1}{n^5} иррациональным.
1. Гипотеза континуума
Верно ли, что между мощностью натуральных чисел (ℵ₀) и мощностью континуума (|ℝ| = 2^{ℵ₀}) нет промежуточных мощностей?
Доказана независимость от аксиом ZFC (Коэн, 1963). Пример: Множество всех подмножеств ℕ имеет мощность 2^{ℵ₀}, но неизвестно, равно ли это ℵ₁. Проблема возникает из-за несчётности ℝ — свойства, отсутствующего в ℚ.
2. Существование неизмеримых множеств
Существуют ли подмножества [0,1] ⊂ ℝ, для которых невозможно определить длину?
Доказано, что в ZFC такие множества существуют (из-за аксиомы выбора). Пример: Множество Витали выбираем по одному элементу из каждого класса эквивалентности x ∼ y ⇔ x-y ∈ ℚ. В ℚ все множества измеримы, так как оно счётно. Неизмеримость является следствием континуума.
3. Неразрешимость равенства вычислимых чисел
Можно ли алгоритмически проверить равенство двух чисел, заданных формулами?
Для элементарных функций задача неразрешима. Пример: Пусть a = ∫_0^1 e^{-x^2} dx, b = √π/2 · erf(1). Доказать a = b алгоритмически невозможно. В ℚ равенство проверяется сравнением p/q = r/s ⇔ p·s = q·r.
4. Трансцендентность чисел
Существует ли алгоритм, определяющий, является ли произвольное вещественное число трансцендентным (не корнем многочлена с целыми коэффициентами)?
Нет общего алгоритма (даже для чисел вида e^π, π^e). Пример: Число e^π трансцендентно (теорема Гельфонда), но для e^e или π^π это неизвестно. В ℚ все числа алгебраические степени 1.
5. Проблема распознавания сходимости
Можно ли алгоритмически определить, сходится ли произвольный несобственный интеграл?
Неразрешима. Даже для интегралов вида ∫_a^b f(x) dx, где f(x) — элементарная функция. Пример: Интеграл ∫_1^∞ sin(x^2) dx сходится, но автоматически это не докажешь. В ℚ нет аналогов несобственных интегралов.
Вещественные числа (ℝ) — это фундамент квантовой механики (уравнение Шрёдингера iℏ ∂ψ/∂t = Ĥψ), теории относительности и криптографии, но их ограниченность проявляется в неразрешимости уравнения x² = -1, что вынуждает перейти к комплексным числам ℂ = {a + bi | a,b ∈ ℝ, i = √-1}, где ℂ становится языком квантовых вычислений (кубиты |ψ⟩ = α|0⟩ + β|1⟩ ∈ ℂ²), электротехники (импеданс Z = R + iX), обработки сигналов (преобразование Фурье) и фрактальной геометрии (Множество Мандельброта z_{n+1} = z_n² + c), объединяя алгебру, анализ и геометрию в формуле Эйлера e^{iπ} + 1 = 0.
Вещественные числа (ℝ) всего лишь четвёртая ступень, но уравнение
x² = -1
неразрешимо в ℝ, что требует расширения до комплексных чисел ℂ = {a + bi | a,b ∈ ℝ, i = √-1}.
Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.