Серия «Аритмомахия (математика и числа) »

1. Подсчитайте количество стульев в аудитории.

2. В коробке 12 карандашей. Сколько карандашей в 5 таких коробках?

3. Найдите НОД (наибольший общий делитель) чисел 36 и 48.

4. Является ли число 101 простым?

5. Сколько существует натуральных решений неравенства x < 10?

6. Решите уравнение: 5x - 7 = 18.

7. Найдите сумму первых 50 натуральных чисел.

8. Делится ли число 7^12 + 3 на 5? (Используйте признаки делимости или модульную арифметику).

9. Решите в натуральных числах: x^2 + y^2 = 25.

10. Почему уравнение x + 8 = 5 не имеет решения в натуральных числах?

От ℕ к ℤ

Представьте ситуацию: у вас есть 3 монеты (x = 3), а долг составляет 5 монет (b = 5). Уравнение, моделирующее погашение долга: x + y = b, или 3 + y = 5, легко решается в N: y = 2 (нужно добавить 2 монеты).

Но что, если ситуация обратная? У вас долг в 3 монеты (x = -3? Но отрицательных чисел в N нет), а вам дали 5 монет (b = 5). Уравнение x + y = b принимает вид: ? + 5 = 5. Как выразить исходный долг? Более наглядно ограничение видно в уравнении типа:

Exempli gratia: x + 8 = 5. Это уравнение принципиально неразрешимо в множестве натуральных чисел (ℕ). В мире ℕ нет такого числа x, которое, будучи прибавленным к 8, даст 5. Потребность оперировать с недостатками, долгами, противоположными направлениями (высота ниже уровня моря, движение назад) привела к расширению до целых чисел (Z), включающих отрицательные числа и ноль. Теперь x = -3 + 8 = 5 вполне решаемо.

1. Температура упала с +5°C до -3°C. На сколько градусов изменилась температура?

2. Решите уравнение: x + 17 = 10.

3. Вычислите: | -15 | + (-8) * 3.

4. Найдите все целые решения неравенства: -4 ≤ 2x < 6.

5. Сумма трех последовательных целых чисел равна -12. Найдите эти числа.

6. Решите уравнение: 3| x - 4 | = 15.

7. Докажите, что квадрат любого целого числа при делении на 4 дает остаток 0 или 1.

8. Найдите остаток от деления (-23)^15 на 5.

9. Решите в целых числах систему: x + y = 10, 2x - y = 4.

10. Почему уравнение 3x = 2 не имеет решения в целых числах?

От ℤ к ℚ

Целые числа (ℤ) прекрасно справляются с задачами, где важны целые противоположности. Однако они бессильны перед необходимостью точного деления на части. Представьте деление 3 целых яблока поровну между 2 людьми. Каждому должно достаться число x, удовлетворяющее уравнению 3x = 2. В множестве целых чисел (ℤ) такого числа x не существует. Ни одно целое число, умноженное на 2, не даст 1. Это ограничение требовало введения дробей, что привело к созданию рациональных чисел (ℚ) — чисел, представимых как отношение двух целых (дробь m/n, где n ≠ 0). Теперь x = 0,15 , что очевидно.

1. Представьте дробь 3/8 в виде десятичной.

2. Сократите дробь: 48/72.

3. Вычислите: (2/5) * (15/8) + (1/2).

4. Решите уравнение: (2/3)x = 5/6.

5. Переведите периодическую дробь 0.1(6) в обыкновенную дробь.

6. Сравните числа: 5/7 и 7/10.

7. Решите уравнение: (x - 1)/3 = (2x + 1)/4.

8. Докажите, что сумма (1/2 + 1/3 + ... + 1/10) не является целым числом.

9. Найдите x, если 60% от x равны 40% от 90.

10. Почему нельзя точно представить длину диагонали единичного квадрата (√2) рациональным числом? (Без строгого доказательства, объясните суть).

От ℚ к ℝ

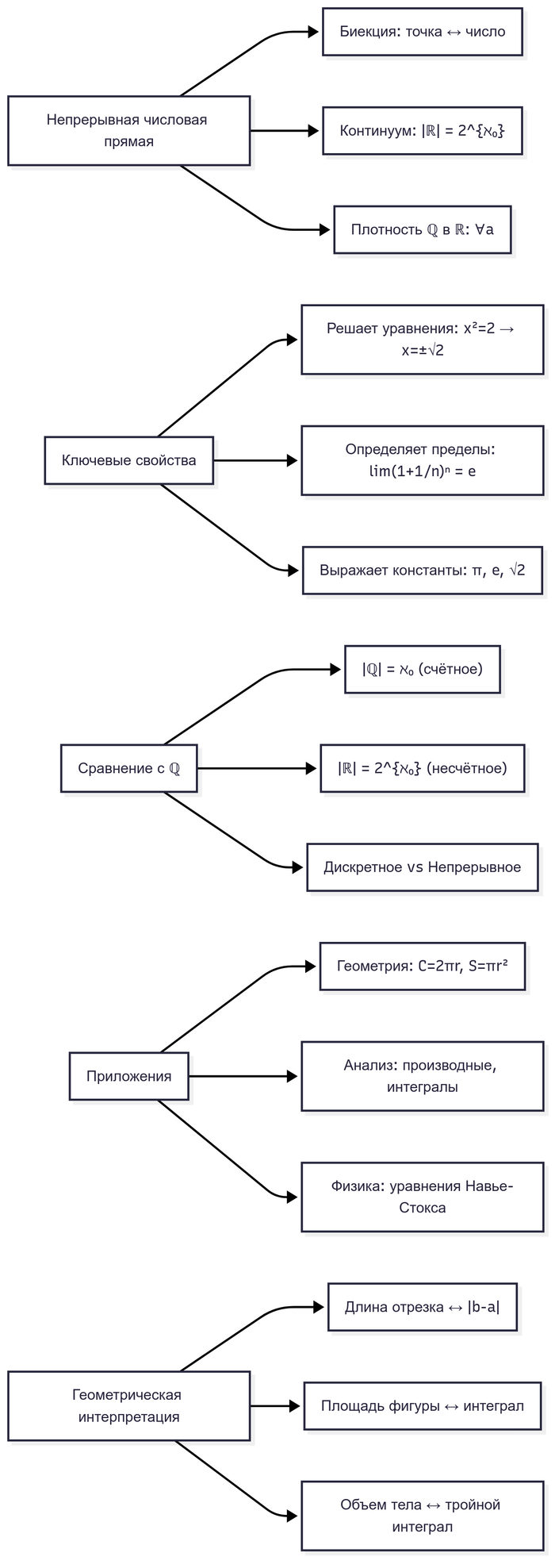
Рациональные числа (ℚ) идеальны для описания точных пропорций. Однако геометрия и анализ сразу указали на их неполноту. Классический пример: отношение длины окружности к её диаметру. Для любой окружности это отношение постоянно и равно числу π (пи). Уравнение, выражающее это: C / D = π. Доказано, что ни одна дробь (никакое рациональное число ℚ) не может точно выразить значение π. Решение x = π существует геометрически (это универсальное отношение для всех окружностей), но не выражается точно никакой конечной или периодической десятичной дробью (что эквивалентно представлению дробью m/n). Это несоответствие между геометрической непрерывностью (кривая окружность) ℚ потребовало введения вещественных чисел (ℝ), включающих иррациональные числа (как π, √2, e), чтобы "заполнить" числовую прямую полностью.

1. Измерьте длину карандаша в сантиметрах (значение будет вещественным).

2. Округлите число π ≈ 3.14159265 до сотых.

3. Решите уравнение: x² = 10 (найдите приближенное значение).

4. Сравните числа: √3 и 1.732.

5. Вычислите площадь круга радиусом R=5 см (S = πR²).

6. Решите уравнение: x³ - 2x² - 5x + 6 = 0 (один корень - целый, найдите его; другие - вещественные).

7. Найдите предел: lim (x → ∞) (3x² + 2x - 5) / (2x² - x + 1).

8. Вычислите: sin(π/3) + log₂(8).

9. Докажите, что уравнение x⁵ - 3x - 1 = 0 имеет вещественный корень на интервале (1, 2).

10. Почему уравнение x^3 - 15x - 4 = 0 не имеет решения в вещественных числах?

От ℝ к ℂ

Вещественные числа (ℝ) создают непрерывную, "сплошную" числовую прямую. Они фундаментальны для математического анализа, физики сплошных сред, описания любых непрерывно изменяющихся величин. Однако алгебра ставит перед ними непреодолимую (в их рамках) преграду. Рассмотрим вышеупомянутое уравнение:

Формально, подставляя вещественные числа, можно найти корень x=4 (4^3 - 15*4 - 4 = 64 - 60 - 4 = 0). Однако применение классической формулы Кардано для решения кубических уравнений в процессе вычислений приводит к необходимости извлечь квадратный корень из отрицательного числа: √(-121) = √(-1 * 11^2) = 11√(-1). В множестве вещественных чисел (ℝ) операция √(-1) не определена — квадрат любого вещественного числа неотрицателен.

Потребность получить вещественный корень (x=4) через формальные алгебраические методы, требующие промежуточных "несуществующих" (с точки зрения ℝ) операций, а также описание колебаний и волн (где комплексные числа кодируют амплитуду и фазу), привела к самому фундаментальному расширению — введению комплексных чисел (ℂ). В них определяется мнимая единица i, такая что i^2 = -1, и числа представляются как a + bi, где a и b — вещественные числа. Это позволяет корректно выполнять промежуточные вычисления (вроде √(-121) = 11i) и получать как комплексные, так и вещественные результаты. Уравнение x^3 - 15x - 4 = 0 имеет вещественный корень x=4, найденный через комплексные числа (ℂ).

1. Решите уравнение: z² = -9.

2. Вычислите: (2 + 3i) + (5 - i).

3. Умножьте: (1 - 2i) * (3 + i).

4. Найдите модуль комплексного числа: -4 + 3i.

5. Представьте число 1 - i в тригонометрической форме (r(cosφ + i sinφ)).

6. Вычислите: i⁴⁵ (используйте периодичность i^n).

7. Решите уравнение: z² - 4z + 13 = 0.

8. Найдите комплексное число z, такое что |z| = 5 и Re(z) = 3.

9. Используя Формулу Эйлера (e^(iφ) = cosφ + i sinφ), вычислите e^(iπ).

10. Объясните, почему комплексные числа удобны для описания переменного тока в электротехнике (качественно: амплитуда и фаза).

Описание синусоидального сигнала переменного тока (например, напряжения U(t) = U₀ * sin(ωt + φ)) требует одновременного учета двух ключевых параметров: амплитуды (U₀) и фазы (φ). Непосредственный анализ цепей, содержащих катушки индуктивности (L) и конденсаторы (C), с использованием таких временных функций приводит к сложным дифференциальным уравнениям из-за зависимости токов и напряжений на этих элементах от производных (скоростей изменения сигнала).

Комплексные числа предоставляют способ преодоления этой сложности.

Во-первых, сигнал представляется комплексной амплитудой (фазором) Ů = U₀ * e^(iφ). Его модуль |Ů| = U₀ хранит амплитуду, аргумент arg(Ů) = φ хранит фазу. Это объединяет два параметра в один объект.

Во-вторых, свойства элементов описываются комплексным сопротивлением: резистор (R): Ż_R = R (действительное, фазы совпадают), катушка (L): Ż_L = i * ωL (мнимое +i, ток отстает на 90°), конденсатор (C): Ż_C = -i/(ωC) (мнимое -i, ток опережает на 90°). Мнимая единица i естественно кодирует фазовые сдвиги.

В-третьих, основные законы принимают алгебраическую форму: закон Ома: Ů = Ż * İ (комплексные напряжение, ток, импеданс), правила Кирхгофа (Σ İ_k = 0, Σ Ů_k = 0) работают аналогично цепям постоянного тока. Это позволяет применять все методы анализа цепей постоянного тока к сложным цепям переменного тока, просто используя комплексные числа.

В-четвёртых, комплексная мощность Š = Ů * İ* компактно дает активную (Re(Š)), реактивную (Im(Š)) и полную (|Š|) мощность.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.

В I веке н.э. Герон Александрийский в "Метрике" столкнулся с квадратным корнем из отрицательного числа при расчете пирамиды, но отбросил результат как "бессмысленный":

Таковая величина не может существовать среди действительных чисел.

Персидский математик Аль-Хорезми (IX век) в "Аль-Джабр" классифицировал квадратные уравнения, но для случаев вроде x² + 1 = 0 писал:

Отрицательное не имеет квадрата, ибо отрицательное не есть число.

Поворотный момент наступил в XVI веке. Джероламо Кардано в "Ars Magna" (1545 г.) формально записал корни кубического уравнения, и назвал их "софистическими" — "более тонкими, чем реальность":

Прорыв совершил Рафаэль Бомбелли в "Алгебре" (1572 г.). Для уравнения Кардано:

Он открыл правила мнимых операций:

Рене Декарт (1637) в "Геометрии" ввел термин "мнимые числа" (nombres imaginaires), противопоставляя их "реальным":

Корни могут быть не всегда реальны, иногда — лишь воображаемы

Леонард Эйлер (1777) установил символ i для √-1 в письме к Лагранжу, и он же вывел формулу e^{iφ} = cos φ + i sin φ, связав анализ и тригонометрию:

Пусть √-1 обозначается буквой i

Каспар Вессель (1799) представил комплексные числа как векторы на плоскости:

"Направленная линия: длина a, угол θ с осью"
Но его работа осталась незамеченной.

А Карл Фридрих Гаусс в работе "Theoria residuorum biquadraticorum" (1799) дал строгое определение:

В XIX век Уильям Гамильтон (1837 г.) формализовал комплексы как пары вещественных чисел:

Карл Вейерштрасс ввел символ ℂ (1893 г., лекции в Берлине), однако его лекции записывали ученики (Гурвиц, Фробениус), и в их конспектах комплексные числа часто обозначаются просто C (латиница) или K (от "komplex"), а не готической ℂ.

Эдмунд Ландау (1917) в книге "Darstellung und Begründung einiger neuerer Ergebnisse der Funktionentheorie" систематически использует ℂ для поля комплексных чисел. Однако Ландау всего лишь популяризовал уже ходивший в Гёттингенском университете (где работали и он, и Вейерштрасс раньше) символ.

Символ ℂ был стандартизирован группой Николя Бурбаки в "Элементах математики" (1939):

Обозначим через ℂ поле комплексных чисел
— Livre II: Algèbre, Ch. 2, §1

Мы не можем отказать себе в удовольствии процитировать Давида Гильберта, провозгласившего:

Введение комплексных чисел [...] придает алгебре ее завершенность и совершенство. [...] Поле комплексных чисел алгебраически замкнуто..

— Hilbert, D. Vorlesungen über Zahlentheorie (1912/13), bearbeitet von S. Gümbel, S. 62.

Множество упорядоченных пар ℂ = { (a, b) } с операциями:

Сложение:

Умножение:

Примеры:

Операции:

Сложение:

Пример: (2, 3) + (1, 4) = (3, 7)

Умножение:

Пример: (0, 1) × (0, 1) = (-1, 0)*

Аксиомы поля:

Сложение — абелева группа:

Ассоциативность: (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)

Коммутативность: z₁ + z₂ = z₂ + z₁

Нейтральный: (0, 0)

Обратный: -(a, b) = (-a, -b)

Умножение (ℂ{0}) — абелева группа:

Обратный: (a, b)⁻¹ = (a/(a² + b²), -b/(a² + b²))

Дистрибутивность: z₁ × (z₂ + z₃) = z₁ × z₂ + z₁ × z₃
Ключевое свойство: Алгебраическая замкнутость (любой многочлен *P(z) = 0* имеет корень в ℂ).

Геометрический смысл

Число z = (a, b) соответствует:

Точке (a, b) на плоскости

Вектору из (0, 0) в (a, b)

Полярной форме: z = r(cos φ + i sin φ) = re^{iφ}
где r = √(a² + b²), *φ = atan2(b, a)*

Применение:

Решение *x² = -1* → x = ±i

Интеграл ∫e^{-x²}dx = √π (через методы ℂ)

Умножение на e^{iφ} → поворот вектора на угол φ

Хотя переход к ℂ устраняет ключевой алгебраический дефект ℝ (разрешая x² = -1), он не преодолевает барьеры неполноты, установленные теоремой Гёделя. Любая достаточно богатая формальная система, способная выразить арифметику ℕ (а ℂ содержит ℕ как подмножество), будет либо неполной (существуют истинные, но недоказуемые утверждения), либо противоречивой. Комплексные числа, будучи алгебраически замкнутыми и метрически полными, остаются бессильны против логических пределов познания.

1. Проблема выразимости корней высших степеней

Уравнения степени ≤4 разрешимы в радикалах (например, x³ - 2 = 0 → x = ³√2), но для x⁵ - x + 1 = 0 общая формула отсутствует принципиально. Теорема Абеля-Руффини (1824): Для многочленов общей формы степени ≥5 не существует решения в радикалах.

2. Проблема идентификации трансцендентных чисел

e^π (число Гельфонда) доказано трансцендентным (теорема Гельфонда–Шнайдера), но для e + π все попытки провалились. Нет алгоритма, определяющего трансцендентность произвольного z ∈ ℂ. Индивидуальные доказательства требуют глубокого анализа. Универсальный метод невозможен из-за бесконечного разнообразия чисел в ℂ.

3. Проблема критической линии дзета-функции

Контрпример — ноль вида 0.4 + i·t — немедленно опровергнет гипотезу. Но даже при |t| > 10³⁰ все нули упорно прилипают к линии Re(s)=0.5. Глубина аналитического аппарата ℂ недостаточна. Требуются принципиально новые связи между анализом и арифметикой.

4. Проблема алгоритмической неразрешимости для систем

Простейшая система z₁² + 1 = 0, z₂² + 1 = 0 разрешима (z₁=±i, z₂=±i), но для z₁³ + z₂³ = z₁z₂ + k (k ∈ ℂ) не существует общего алгоритма проверки разрешимости. Теорема Мухина (1977): Проблема разрешимости диофантовых уравнений в ℂ для n≥2 переменных алгоритмически неразрешима.

5. Проблема вычислительной катастрофы

Уравнение x² - 4x + 4 = 0 имеет корень x=2 (кратности 2). Но при ничтожном возмущении:
x² - (4 + 10^{-10})x + 4 = 0 → корни 2 + 5·10^{-11} ± i·\sqrt{10^{-10}}. Малая погрешность в коэффициенте (10^{-10}) порождает катастрофическую мнимую компоненту (≈ 0.0003i), хотя исходно корни вещественны. Погрешности в ℝ и неадекватность моделей вычислений для ℂ делают точные результаты фикцией для сложных задач.

Комплексные числа (ℂ) служат базисом квантовой физики и электродинамики. Волновые функции (основа квантовой механики) записываются как Ψ = Re^{iθ}, где амплитуда R и фаза θ описывают состояние частицы. Уравнения Максвелла для электромагнитных полей требуют ℂ для компактной записи гармонических полей: E⃗ = E₀e^{i(ωt - kz)}. В криптографии на изогениях (SIDH, постквантовые алгоритмы) группы точек эллиптических кривых над ℂ обеспечивают стойкость к атакам.

Безусловно, комплексные числа (ℂ) не конечная позиция в иерархии чисел. Хотя ℂ алгебраически замкнуты (любой многочлен имеет корень), существуют уравнения, требующие более сложных систем. Для некоммутативных задач кватернионы (ℍ), для неассоциативных задач октонионы (𝕆), для альтернативной метрики p-адические числа (ℚₚ), для многомерной физики алгебры Клиффорда, для инфинитезималей гипердействительные числа (*ℝ).

Wenn ℕ die Bausteine des Universums sind,
ℤ die Gesetze des Gleichgewichts,
ℚ die Kunst des Messens,
ℝ das Gewebe der Kontinuität,
dann ist ℂ — der Spiegel der mehrdimensionalen Realität,
wo Algebra, Geometrie und Physik verschmelzen
in der Harmonie von Eulers Formel:

e^{iπ} + 1 = 0

- Arithmomachia von Paulus Preisghausen.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.

Древний мир столкнулся с загадкой непрерывности через геометрию. Пифагорейцы (V в. до н.э.), открыв иррациональность √2, пытались скрыть это:

Гиппас из Метапонта был изгнан за доказательство, что диагональ квадрата несоизмерима со стороной
— Ямвлих, "О пифагорейской жизни".

Это было связано с тем, что пифагорейцы обожествляли целые числа и их отношения. Их доктрина гласила:

Всё сущее есть число,

подразумевая, что любую величину (длину, площадь, гармонию) можно выразить дробью p/q. Открытие, разрушившее эту веру, возникло при изучении диагонали квадрата со стороной 1. оказалось, что никакая дробь не укладывается точно ни в диагональ, ни в сторону. Гиппас предположил, что 2=pq2=qp (дробь несократима). Тогда:

Отсюда:

Дробь оказалась сократимой. Пифагорейцы назвали такие числа "алогон" (невыразимое).

Античный ответ дал Евдокс Книдский (IV в. до н.э.). В "Началах" Евклида (Книга V) он создал теорию пропорций для величин любой природы:

Говорят, что величины находятся в том же отношении a:b = c:d, если равны их кратные: m·a > n·b ⇔ m·c > n·d.

Средневековый Восток приблизился к идее предела. Ал-Каши (XV в.) в "Ключе арифметики" вычислял π с 16 знаками, разбивая окружность на 805 306 368 частей.

Длина полуокружности диаметра 1 есть 3;1415926535897932...

Для этого он вписал в окружность правильный многоугольник с 805 306 368805306368 сторонами, последовательно удваивая число сторон и вычисляя длину каждой новой стороны через предыдущую:

Результат записал как: π ≈ 3;8 29 44 0 47 25 53 7 25 (в шестидесятеричных долях). Стоит отметить, что его метод предвосхитил интегральное исчисление.

Перелом наступил в XVII веке. Бонавентура Кавальери в "Геометрии неделимых" (1635) представлял площади как суммы бесконечно тонких линий:

Фигура — ткань из всех своих сечений, как ткань — из нитей.

Exempli gratia: необходимо вычислить площадь круга радиуса R. Для этого круг разрезается на n бесконечно тонких колец толщиной dx. Площадь кольца на расстоянии x от центра:

Суммируя:

Ньютон в "Методе флюксий" (1671) пошел дальше:

Величины исчезающе малые суть пределы отношений приращений.

Флюэнта (x) — изменяющаяся величина (например, координата). Флюксия (ẋ) — скорость изменения (производная).

XIX век дал ℝ аксиоматический фундамент. Рихард Дедекинд в "Непрерывность и иррациональные числа" (1872) ввел сечения:

Если все рациональные числа разбиты на два класса так, что каждый элемент первого класса меньше любого элемента второго — это сечение определяет вещественное число.

Его современник, Георг Кантор, построил ℝ через фундаментальные последовательности:

Число есть класс эквивалентности последовательностей Коши в ℚ.

А Карл Вейерштрасс, в свою очередь, завершил процесс:

Вещественные числа суть полное архимедово упорядоченное поле.

До XX века вещественные числа не имели универсального символа. В трудах Коши (1821) они назывались quantités, у Вейерштрасса (1860-е) reelle Zahlen, у Гильберта (1899) kontinuum. Перелом наступил в 1939 году, когда группа французских математиков под псевдонимом Николя Бурбаки выпустила IV том "Éléments de mathématique".

Обозначим через ℝ совершенное тело, порожденное топологией прямой
— Элементы математики, Т. IV.

В лекции "О бесконечном", в 1925 году, Давид Гильберт, защищая теорию множеств Кантора от критики математиков0интуицинистов, вроде Л. Э. Я. Брауэра, сказал:

Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können.

- Gesammelte Abhandlungen, Bd. 3, S. 170

Вещественные числа (ℝ) строятся как пополнение рациональных чисел, заполняющее принципиальные пробелы в числовой прямой. Основными конструкциями являются:

Сечения Дедекинда (1872):

Пример:

Фундаментальные последовательности Коши (Кантор, 1872):

Примеры:

Операции

Сложение:

Пример:

Умножение:

Пример:

Аксиомы алгебраической структуры (наследуются от ℚ):

Сложение — абелева группа:

Ассоциативность: (a+b)+c = a+(b+c)

Нулевой элемент: a+0 = a

Противоположный элемент: a + (-a) = 0

Умножение (ℝ{0}) — абелева группа:

Обратный элемент: a · a^{-1} = 1

Дистрибутивность: a · (b+c) = a·b + a·c

Аксиомы порядка:

Трихотомия: ∀a,b ∈ ℝ: (a < b) ∨ (a = b) ∨ (a > b)

Монотонность:

a < b ⇒ a + c < b + c

a < b, c > 0 ⇒ a·c < b·c

Аксиома полноты (ключевое отличие!):

Пример: A = {x ∈ ℚ | x² < 2} имеет sup A = √2 ∉ ℚ.

Геометрический смысл

Непрерывная числовая прямая: каждой точке прямой взаимно однозначно соответствует вещественное число.

Континуум: мощность |ℝ| = 2^{ℵ_0} (несчётное множество), тогда как |ℚ| = ℵ_0 (счётное множество).

Вещественные числа (ℝ) связаны с рациональными (ℚ) через вложение (f: ℚ → ℝ, f(r) = [{r, r, r, ...}]) и плотность (∀a,b ∈ ℝ (a < b) ∃r ∈ ℚ: a < r < b)

Пример: между √2 ≈ 1.414 и 1.415: 1.4145 = 2829/2000.

Расширение до вещественных чисел решило проблемы ℚ с корнями уравнений и пределами, однако это не устраняет принципиально новые вызовы:

Во-первых, почти все вещественные числа не имеют алгоритмического описания: вычислимые числа (задаваемые программой) образуют счётное множество (|выч. чисел| = |ℕ| = ℵ₀) и мощность ℝ — континуум (|ℝ| = 2^{ℵ₀}) приводит к тому, что ⇒ >99.9% чисел в ℝ не выразимы формулами, не вычислимы на практике.

Пример:

Константа Ω (Хайтина):

Во-вторых, невозможно создать корректную универсальную запись из-за неединственности (0.999... = 1.000... (дуализм в десятичной системе)), неполноты (в любой системе счисления большинство чисел требуют бесконечных дробей: 1/3 = 0.333..._{10} = 0.010101..._2) и парадокса: число π нельзя точно записать даже в системе счисления с иррациональным основанием.

В-третьих, для чисел, заданных алгоритмически,

не существует алгоритма, проверяющего a = b, поэтому открыт вопрос об иррациональности e + π (хотя доказано, что min(e+π, e·π) иррационально).

В-четвёртых, любая аксиоматизация ℝ (напр., теория вещественно замкнутых полей) неполна, так как существуют утверждения вида:

которые недоказуемы и неопровержимы.

Пример: гипотеза Континуума (2^{ℵ₀} = \aleph_1) независима от ZFC.

В-пятых, простые действия становятся неразрешимыми:

Сравнение: Для вычислимых a, b задача a < b не имеет общего алгоритма.

Интегрирование: Проверка \int_a^b f(x) dx = 0 неразрешима для элементарных f(x) (теорема Ричардсона, 1968).

Контрпример: \int_0^1 \frac{\sin x}{x} dx = \text{Si}(1) — значение неизвестно.

В-шестых, при аксиоме выбора существуют неизмеримые множества, exempli gratia построение Витали: разбиение [0,1] на сдвиги по ℚ ∩ [-1,1]. Невозможно определить длину таких множеств, что ставит под сомнение применимость ℝ в физике.

В-седьмых, большинство чисел в ℝ трансцендентны. Известно примерно 50 таких чисел (e.g., e, π, e^\pi). Нет алгоритма проверки трансцендентности для выражений:
\alpha = \pi + e, \quad \beta = \pi^{\sqrt{2}}. Неизвестно, является ли \zeta(5) = \sum_{n=1}^{\infty} \frac{1}{n^5} иррациональным.

1. Гипотеза континуума

Доказана независимость от аксиом ZFC (Коэн, 1963). Пример: Множество всех подмножеств ℕ имеет мощность 2^{ℵ₀}, но неизвестно, равно ли это ℵ₁. Проблема возникает из-за несчётности ℝ — свойства, отсутствующего в ℚ.

2. Существование неизмеримых множеств

Доказано, что в ZFC такие множества существуют (из-за аксиомы выбора). Пример: Множество Витали выбираем по одному элементу из каждого класса эквивалентности x ∼ y ⇔ x-y ∈ ℚ. В ℚ все множества измеримы, так как оно счётно. Неизмеримость является следствием континуума.

3. Неразрешимость равенства вычислимых чисел

Для элементарных функций задача неразрешима. Пример: Пусть a = ∫_0^1 e^{-x^2} dx, b = √π/2 · erf(1). Доказать a = b алгоритмически невозможно. В ℚ равенство проверяется сравнением p/q = r/s ⇔ p·s = q·r.

4. Трансцендентность чисел

Нет общего алгоритма (даже для чисел вида e^π, π^e). Пример: Число e^π трансцендентно (теорема Гельфонда), но для e^e или π^π это неизвестно. В ℚ все числа алгебраические степени 1.

5. Проблема распознавания сходимости

Неразрешима. Даже для интегралов вида ∫_a^b f(x) dx, где f(x) — элементарная функция. Пример: Интеграл ∫_1^∞ sin(x^2) dx сходится, но автоматически это не докажешь. В ℚ нет аналогов несобственных интегралов.

Вещественные числа (ℝ) — это фундамент квантовой механики (уравнение Шрёдингера iℏ ∂ψ/∂t = Ĥψ), теории относительности и криптографии, но их ограниченность проявляется в неразрешимости уравнения x² = -1, что вынуждает перейти к комплексным числам ℂ = {a + bi | a,b ∈ ℝ, i = √-1}, где ℂ становится языком квантовых вычислений (кубиты |ψ⟩ = α|0⟩ + β|1⟩ ∈ ℂ²), электротехники (импеданс Z = R + iX), обработки сигналов (преобразование Фурье) и фрактальной геометрии (Множество Мандельброта z_{n+1} = z_n² + c), объединяя алгебру, анализ и геометрию в формуле Эйлера e^{iπ} + 1 = 0.

Вещественные числа (ℝ) всего лишь четвёртая ступень, но уравнение

неразрешимо в ℝ, что требует расширения до комплексных чисел ℂ = {a + bi | a,b ∈ ℝ, i = √-1}.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.

Древний мир заложил основы дробей через практические нужды. В Египте (1650 г. до н.э.) папирус Ахмеса содержал задачи на аликвотные дроби — суммы вида 1/n.

Разделить 7 хлебов на 10 человек. Ответ: ½ + ⅕

Дроби записывались иероглифом "рта" (𓂋) над числом: 𓂻𓏤 = 1/4.

Вавилоняне (1800 г. до н.э.) использовали шестидесятеричные дроби в астрономии: табличка Plimpton 322 показывает диагональ квадрата как 1;24,51,10 (≈√2). В Индии (III в. до н.э.) "Шульба-сутры" описывали дроби a/b (дроби-раши), а Брахмагупта в VII веке формализовал правила:

Сумма дробей: числители сложи, знаменатели умножь
— "Брахмаспхута-сиддханта", гл. 12.

Античность пережила кризис, когда математика столкнулась с иррациональностью. Пифагорейцы (V в. до н.э.) верили, что всё сущее есть отношение целых чисел. Открытие Гиппасом иррациональности √2 вызвало удивление:

Пифагор приказал утопить Гиппаса, ибо доказал он то, чего не должно быть: число диагонали невыразимо дробью
— Ямвлих, "О Пифагоровой жизни".

Ответом Евклида стала строгая теория пропорций в "Началах" (III в. до н.э.):

Числа a и b пропорциональны c и d, если a·d = b·c

(аксиома эквивалентности пар для ℚ).

Средневековый Восток и Европа разработали символику рациональных чисел. Аль-Хорезми (IX в.) в "Китаб аль-Джабр" ввёл арабский термин "каср" (дробь):

Дробь — часть единицы, записанная как числитель над знаменателем.

Фибоначчи (1202 г.) в "Книге абака" популяризировал дроби в Европе, записывая 2 3 для ²⁄₃:

Число ²⁄₃ зовётся двумя третями и означает: взять две части из трёх.

Научная революция XVI-XVII веков возвела ℚ в ранг универсального инструмента. Симон Стевин в трактате "Десятина" (1585 г.) доказал мощь десятичных дробей:

3@1@7@5 столь же совершенно, как 3175, ибо каждый знак после @ есть десятая часть предыдущего

(здесь @ — прообраз десятичной запятой). Ньютон в "Методе флюксий" (1671 г.) использовал рациональные дроби для описания производных:

Флюксия отношения двух величин равна отношению их флюксий

XIX век дал ℚ строгую алгебраическую основу. Рихард Дедекинд определил рациональные числа как фактор-множество пар целых чисел:

Его работа включила ℚ в теорию полей — структур с замкнутыми операциями +, −, ×, ÷. Ключевым свойством стала бесконечная плотность:

Между любыми p/q и r/s найдётся дробь (p+r)/(q+s).

Как писал Дедекинд:

ℚ подобно роялю, на котором можно сыграть многие мелодии, но не все.

- Stetigkeit und irrationale Zahlen, 1872

Именно эти ограничения откроют дорогу к вещественным числам — следующей ступени великой иерархии.

Символ ℚ ввёл Гастон Жюлиа (1930-е гг.) в честь итал. quoziente ("частное"):

Обозначим через ℚ множество всех отношений p\q, где p,q — целые, q≠0
- Julia G. Cours d’analyse. Tome III. Théorie des nombres (1938). Archives du Collège de France, cote F-G-68.

Рациональные числа формально определяются как классы эквивалентности пар целых чисел (a,b), где b≠0:

Примеры:

Операции:

Сложение:

Пример: (1, 2) + (1, 3) = (1*3 + 2*1, 2*3) = (5, 6) = 5/6.

Умножение:

Пример: (3, 2) × (1, 3) = (3*1, 2*3) = (3, 6) = 1/2.

Геометрический смысл:

Каждая дробь a/b соответствует наклону прямой через точки (0, 0) и (b, a) на координатной сетке ℤ × ℤ.

Q — это поле (коммутативное кольцо с обратными элементами для умножения).

Аксиомы:

Сложение

1. Ассоциативность: ∀a,b,c ∈ ℚ: (a+b)+c = a+(b+c)

2. Коммутативность: ∀a,b ∈ ℚ: a+b = b+a

3. Нейтральный элемент: ∀a ∈ ℚ: a+0 = a

4. Обратный элемент: ∀a ∈ ℚ ∃ (-a) ∈ ℚ: a + (-a) = 0

Умножение

1. Ассоциативность: ∀a,b,c ∈ ℚ: (a·b)·c = a·(b·c)

2. Коммутативность: ∀a,b ∈ ℚ: a·b = b·a

3. Нейтральный элемент: ∀a ∈ ℚ: a·1 = a

4. Обратный элемент: ∀a ∈ ℚ (a ≠ 0) ∃ a⁻¹ ∈ ℚ: a · a⁻¹ = 1

Дистрибутивность

∀a,b,c ∈ ℚ: a·(b+c) = a·b + a·c

В отличие от ℤ, в ℚ есть обратные по умножению (для a ≠ 0), нет аналога аксиомы индукции и ZZ вкладывается в QQ как подмножество: a∈Z↦a1a∈Z↦1a.

Чтобы ввести линейный порядок, добавляют:

Трихотомия: ∀a,b ∈ ℚ верно ровно одно: a < b, a = b, a > b.

Монотонность сложения: a < b ⇒ a + c < b + c.

Монотонность умножения: a < b и c > 0 ⇒ a·c < b·c.

Пример: 1/2 < 2/3, так как 2/3 - 1/2 = 4/6 - 3/6 = 1/6 > 0.

Целые числа отождествляются с подмножеством ℚ через отображение:

Расширение до рациональных чисел решает фундаментальные алгебраические проблемы ℤ, но не преодолевает барьеры, установленные теоремой Гёделя о неполноте.

Во-первых, уравнение b·x = a разрешимо в ℚ для любых a, b ∈ ℤ (b ≠ 0).

Пример: 2x = 1 → x = 1/2 (в ℤ решение отсутствует).

Во-вторых, между любыми двумя рациональными числами лежит бесконечно много других рациональных чисел.

Пример: Между 1/2 и 2/3 есть 3/5, 5/8, и т.д.

В-третьих, в тоже время гипотезы о свойствах ℕ (например, проблема Гольдбаха) остаются неразрешимыми в рамках ℚ.

В-четвёртых, хотя ℚ "простая" структура (счётное поле), она так же приводит к глубоким проблемам:

1. Существование иррациональных чисел

Доказательство от противного. Если (p/q)^2 = 2, то p^2 = 2q^2. Это противоречит единственности разложения на простые множители в ℤ.

Примечание: мы углубимся в трансцендентную природу иррациональных чисел в последующих пунктах.

2. 10-я проблема Гильберта для ℚ

Пример: Уравнение x^n + y^n = z^n имеет решения в ℚ при n=1,2, но при n>2 их нет (Великая теорема Ферма).

3. Гипотеза Бёрча — Свиннертон-Дайер (BSD)

Примечание: в ℤ BSD подчёркивает алгоритмическую неразрешимость предсказания существования решений (пример гёделевской неполноты через диофантовы уравнения), в то время как в ℚ BSD акцентирует фундаментальную недоказуемость структуры бесконечных множеств (групп), определённых простыми уравнениями.

4. Проблема конечности множества решений

Но нет общего алгоритма для произвольного многочлена.

5. Алгоритмическая сложность арифметики ℚ

Вычисление 1234567/9876543 + 876543/1234567 приводит к числам с 14 знаками.

Рациональные числа (ℚ) — служат основой для алгоритмов на эллиптических кривых (ECC), обеспечивающих защиту интернета и блокчейн-систем (Биткоин, Ethereum), целиком основанных на арифметике рациональных точек. Постквантовая криптография (PQC) исследует алгебраические многообразия, определённые над ℚ, требуя точных вычислений с рациональными числами. В прикладных областях, финансовом моделировании, инженерных расчётах (метод конечных элементов) и физическом моделировании (решёточные газы), ℚ выступает стартовой базой для точного представления величин перед переходом к вещественным (ℝ) приближениям.

Рациональные числа (ℚ) — всего лишь третья ступенька в иерархии. Уравнение

неразрешимо в рациональных числах. Это приведёт нас к вещественным числам (ℝ), мосту между дискретностью и континуумом.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.

Мир натуральных чисел (ℕ), мир счёта, сложения и умножения, казался древним математикам полным и самодостаточным. Однако сама жизнь ставила задачи, которые ℕ решить не могли:

Как выразить долг? Как формализовать убыль? Как решить уравнение x + 5 = 3?

Ответом стало появление целых чисел (ℤ), расширивших ℕ включением отрицательных чисел и нуля как полноценного объекта:

Практические истоки целых чисел находятся в древних цивилизациях. В Китае эпохи Хань (200 г. до н.э.) трактат "Цзючжан Суаньшу" ввёл палочки двух цветов: красные для прибыли (正), чёрные для долга (負). Запись 赤三 黑五 (красные 3, чёрные 5) означала чистый долг в 2 единицы — прообраз -2.

В Индии V-VII вв. Брахмагупта в "Брахмаспхута-сиддханте" формализовал ноль и арифметику:

Хотя его попытка определить 0/0 = 0 была ошибочна, это смело расширило горизонты. Через исламский мир (аль-Хорезми, VIII-IX вв.) эти идеи достигли Европы, но встретили сопротивление.

Декарт в XVII веке называл отрицательные корни "ложными",

...но часто случается, что некоторые из этих корней ложны или меньше, чем ничто.
La Géométrie, 1637

а Паскаль отвергал вычитание 4 из 0 как абсурд:

...я понимаю, что можно обозначить долг знаком минус [...], но как можно представить величину меньшую, чем ничто?
Lettres de Pascal à Fermat, 1654

Перелом наступил лишь когда координатная прямая Декарта дала отрицательным числам геометрическую интерпретацию: точки левее нуля.

..и чтобы отличать эти равные, но противоположные по знаку числа, если корни истинные [положительные], я пишу их сразу после с знаком +; а если ложные [отрицательные], то с знаком -.

La Géométrie, 1637

Философский триумф целых чисел состоялся в XVIII-XIX веках. Леонард Эйлер в трудах по алгебре легитимировал операции с отрицательными числами,

Следовательно, ясно, что произведение -a на -b должно быть таким же, как произведение a на b, а именно +ab. ... Следовательно, если говорят, что -3 умножить на -4 дает +12, то это верное правило.)

Vollständige Anleitung zur Algebra, 1770

а Уильям Гамильтон включил ℤ в структуру коммутативного кольца (термин "коммутативное кольцо" появился позже, в 1897 у Д. Гильберта "Zahlbericht", формализован в 1921 Э. Нетёр "Idealtheorie in Ringbereichen" и устоялся в 1930 Б. ван дер Варденом "Moderne Algebra"), где каждое число имеет противоположное (a + (-a) = 0), а ноль стал нейтральным элементом (a + 0 = a, a × 0 = 0).

Ключевой скачок был не в символах, а в качественном преодолении ограничений ℕ:

1) Уравнение x + a = b разрешимо при любых a, b,

2) Появилась симметрия (-a как "зеркало" a),

3) Числа абстрагировались от контекста: -5 — не только долг, но и температура, смещение, заряд.

Как подчеркнул Герман Ганкель, это воплотило "принцип перманентности": законы ℕ сохранились при расширении до ℤ.

Если две формы, выраженные в общей арифметике, равны, то они должны оставаться равными и тогда, когда входящие в них символы перестают обозначать простые величины, и, следовательно, операции приобретают более общее содержание.

Объясним суть принципа на практике:

Возьмём сходный закон для ℕ, exempli gratia, дистрибутивность: a × (b + c) = a×b + a×c.

Расширение до ℤ:

При добавлении отрицательных чисел и нуля возник ключевой вопрос:

Как определить операции для новых объектов, чтобы старые правила не рухнули?

Пример с умножением:

Для натуральных 3 × 2 = 6.

Чтобы сохранить дистрибутивность в ℤ, пришлось принять:

Так дистрибутивность потребовала положительное × отрицательное = отрицательное.

Принцип работает, только если новые объекты не создают парадоксов. Например, в ℤ сохранилось a × 0 = 0, но деление на ноль запрещено — оно разрушает структуру (1 = 2 и т.д.).

В прошлом посте мы обещали рассмотреть историю нуля подробнее. История нуля, напомним, началась с ранних форм-заполнителей пустоты (с 3000 г. до н.э.). Вавилоняне использовали двойной клин (˅˅) в шестидесятеричной системе (например, 1˅˅3 = 1×60² + 0×60 + 3), но это был лишь символ пропуска разряда, а не число.

Древние Китай и Египет оставляли пустые места в записях (например, 4‿5 для 405), не создавая отдельного символа.

Революция произошла в Индии (III–IX вв.). В манускрипте Бакхшали (III–IV вв.) обнаружен древнейший символ нуля — жирная точка (●), служившая заполнителем в расчётах. Математик Брахмагупта в 628 г. в труде "Брахмаспхута-сиддханта" впервые определил ноль как число:

Символ превратился в кружок с именем "шунья" (санскр. "пустота"). Через арабов (Аль-Хорезми, IX в.) система распространилась в Европу: арабское "сыфр" (صفر) дало термины "цифра" и "шифр", а итальянцы преобразовали его в "zero".

В Европе (XII–XVII вв.) ноль встретил сопротивление.

Церковь объявила его "дьявольским", ссылаясь на Аристотеля, отрицавшего пустоту. Однако купцы тайно использовали ноль в расчётах, а Фибоначчи в 1202 г. описал его в "Книге абака". К XV веку с развитием книгопечатания ноль узаконился. Научный прорыв совершил Декарт в XVII веке, сделав ноль началом координат в системе осей (x, y), что заложило основы аналитической геометрии и матанализа.

Хотя аксиомы Пеано описывают натуральные числа (ℕ), целые числа (ℤ) требуют более сложной структуры. Их можно построить двумя путями: расширением ℕ или независимой аксиоматизацией. Рассмотрим оба подхода.

1. Построение ℤ из ℕ через классы эквивалентности

Целые числа формально определяют как упорядоченные пары натуральных чисел (разность как абстракция):

Пример: (5, 3) ∼ (2, 0), так как 5 + 0 = 3 + 2 → обе пары кодируют число 2. Или (3, 5) ∼ (0, 2) → кодируют -2. Ноль: класс пар вида (a, a) (например, (4, 4) = 0).

Операции:

Сложение: (a,b) + (c,d) = (a+c, b+d),

Умножение: (a,b) × (c,d) = (ac+bd, ad+bc).

2. Аксиоматизация как коммутативного кольца

ℤ можно задать аксиомами алгебраической структуры (кольца). Основные аксиомы:

Сложение

Умножение

Дистрибутивность

Отсутствие делителей нуля

В ℤ есть симметрия (для каждого элемента существует противоположный), нет аксиомы индукции (она заменяется структурой кольца) и ℤ содержит ℕ как подмножество натуральных чисел (1, 2, 3, ...).

Отдельно отметим аксиомы порядка для ℤ

Чтобы ввести сравнение целых чисел, добавляют:

Трихотомия: ∀a,b ∈ ℤ верно ровно одно: a < b, a = b, a > b.

Монотонность сложения: a < b ⇒ a + c < b + c.

Монотонность умножения: a < b ∧ c > 0 ⇒ a·c < b·c.

Как ℕ вкладывается в ℤ?

Существует изоморфное вложение f: ℕ → ℤ, сохраняющее операции:

Так натуральные числа становятся подмножеством ℤ:

Введение целых чисел (ℤ) расширяет арифметику натуральных чисел (ℕ), но не преодолевает принципиальные ограничения, установленные теоремой Гёделя о неполноте. Рассмотрим причины.

Во-первых, почему ℤ не "сильнее" ℕ для теоремы Гёделя?
Целые числа строятся из натуральных через классы эквивалентности пар (например, (a, b) ∼ (c, d) ⇔ a + d = b + c). Любое утверждение о ℤ можно выразить в терминах ℕ. Если система аксиом для ℕ (Пеано) неполна, то её расширение до ℤ, основанное на тех же принципах, также будет неполным. Теорема Гёделя применима ко всем системам, содержащим арифметику ℕ.

Во-вторых, однако, расширение до целых чисел решает конкретные алгебраические проблемы, но не затрагивает "неуловимость" гёделевских утверждений:

Разрешимость уравнений:

Недоказуемость мета-утверждений:

В-третьих, как и для натуральных чисел, так и для целых существуют принципиальные задачи или парадоксы, демонстрирующие сложность данной числовой системы.

1. Уравнение Пелля (x² - dy² = 1) и его фундаментальные решения

Хотя известно, что существует бесконечно много решений (фундаментальное решение порождает их все алгоритмически), нахождение самого фундаментального решения для произвольного d не имеет известной эффективной формулы. Его "размер" (величина x и y) может быть астрономически огромным даже для умеренных d, что делает проблему вычислительно трудной. Задача упирается в тонкую арифметику колец целых алгебраических чисел, выходящую за рамки элементарной арифметики ℤ.

2. Проблема остановки для целочисленных линейных программ

Проблема остановки даже для этого подкласса программ алгоритмически неразрешима. Это следствие неразрешимости общей 10-й проблемы Гильберта (доказанной Матиясевичем). Не существует алгоритма (и, следовательно, не может быть доказательства в достаточно сильной формальной системе, охватывающей ℤ), которое для любой такой программы и любого начального состояния целочисленных переменных корректно ответило бы, достигнет ли программа состояния остановки. Это конкретная неразрешимая проблема, живущая внутри ℤ.

3. Гипотеза Бёрча — Свиннертон-Дайер (BSD)

Это одна из "Проблем тысячелетия". Доказательство (или опровержение) гипотезы BSD даже для кривых ранга 0 и 1 остается недостижимым. Она требует синтеза глубоких теорий (модулярные формы, L-функции, теория групп), выходящих далеко за рамки аксиоматики кольца целых чисел. Ее статус подчеркивает, что даже "естественные" вопросы о диофантовых уравнениях (частный случай — точки кривой с целыми/рациональными координатами) в ℤ могут быть невероятно сложными и, возможно, неразрешимыми в рамках "элементарных" систем.

4. Задача о представимости множеств полиномами над ℤ (проблема Диофанта , теорема Матиясевича):

Теорема Матиясевича (решившая 10-ю проблему Гильберта негативно) показывает, что существуют алгоритмически неразрешимые множества целых чисел (например, множество номеров машин Тьюринга, останавливающихся на пустом вводе), которые тем не менее являются диофантовыми! Это означает, что для такого множества M существует полином P, как описано выше, но нет алгоритма (и не может быть доказательства в достаточно сильной формальной системе, основанной на ℤ), который по произвольному x ∈ ℤ корректно определил бы, принадлежит ли x множеству M. Это прямой пример гёделевской неполноты, воплощенный внутри арифметики целых чисел через диофантовы множества.

5. Проблема Фробениуса для n > 2 чисел:

Для n=2 существует простая формула: g(a, b) = a·b - a - b. Однако для n >= 3 не существует общей замкнутой формулы для g(a₁, a₂, ..., aₙ). Более того, вычисление g для произвольного набора из n >= 3 чисел является NP-трудной задачей. Хотя это и не прямая недоказуемость в смысле Гёделя, это демонстрирует фундаментальную вычислительную сложность, присущую даже сравнительно простым комбинаторным задачам в ℤ. Невозможность найти общую эффективную формулу или алгоритм подчеркивает ограниченность наших возможностей предсказать поведение систем в ℤ.

Целые числа (ℤ) являются фундаментом цифровой эпохи: они лежат в основе криптографии (протоколы ZKP, zk-SNARKs), компьютерных систем (дополнительный код, координатные сетки) и точных наук (квантовые вычисления, инженерия).

Но даже ℤ недостаточно. Уравнение

неразрешимо в целых числах. Этот вызов приведёт нас к миру рациональных чисел (ℚ), следующей ступени великой иерархии ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.

Готовы отправиться в путешествие от камешков до квантовых волн?
Начнем с самого основания, мира натуральных чисел (ℕ).

История натуральных чисел началась с практических потребностей древних цивилизаций. Зарубки на костях Ишанго, сделанные около 20 000 лет до н.э., свидетельствуют о первых попытках счета скота, урожая или дней. Шумеры (IV тысячелетие до н.э.) использовали числа для учета зерна, скота и налогов, а вавилоняне применяли их в астрономических расчетах движения планет уже во II тысячелетии до н.э.

Эти числа, 1, 2, 3 и далее, стали фундаментом математики, и ноль долгое время не входил в их состав. Но отсутствие нуля было лишь частью решения более сложных задач.

Вавилоняне и майя использовали ноль как позиционный символ, но не считали его числом. В Европе ноль признали лишь в XII веке благодаря трудам Аль-Хорезми, хотя Аристотель отвергал его, утверждая, что

...природа не терпит пустоты.

К вопросу о нуле мы ещё вернёмся в следующих статьях.

Натуральные числа не могли решить уравнения типа x+3=1x+3=1 или корректно выразить результат деления 5 на 3, что позже привело к созданию целых и рациональных чисел. Античные философы, такие как Зенон, оспаривали саму возможность бесконечности ℕ, а средневековые теологи спорили, может ли Бог создать "наибольшее натуральное число".

Формализация ℕ завершилась в XIX веке. Пифагорейцы (V в. до н.э.) пытались свести мир к целым числам, но открытие иррациональности √2 разрушило эту идею.

В 1889 году Джузеппе Пеано создал строгую аксиоматику:
1. 1 ∈ ℕ;
2. ∀n,m∈N(S(n)=S(m)⇒n=m) (инъективность функции следования, т. е. каждое число имеет последующее);
3. ∀n∈NS(n)≠1 (непредикативность 1, т. е. 1 не следует ни за каким числом);
4. [P(1) ∧ ∀k (P(k)⇒P(S(k)))]⇒∀n P(n) (принцип математической индукции, т. е. равенство последующих элементов влечет равенство самих чисел);
Аксиоматика Пеано (в вариантах с 0 или 1) остаётся стандартом.

Теоремы Курта Гёделя навсегда изменили наше понимание математики, показав принципиальные ограничения формальных систем. Применительно к натуральным числам их суть такова: любая достаточно мощная и непротиворечивая система аксиом (включая аксиомы Пеано) неспособна полностью охватить все истинные свойства натуральных чисел.

1. "Машина Тьюринга с номером n не останавливается на пустом вводе".
   Это утверждение истинно для некоторых n (если машина действительно не останавливается) и недоказуемо в аксиомах Пеано. Такие утверждения относятся к конкретным свойствам натуральных чисел (номерам алгоритмов).

   2. Натуральные числа обладают интуитивно ясными свойствами: бесконечность ряда 1,2,3,…1,2,3,…, корректность рекурсивных определений (сложение, умножение). Но никакая формальная система не может полностью захватить эту интуицию. Всегда останутся истины, невыводимые из аксиом.

   3. Гипотезы в теории чисел могут быть принципиально недоказуемыми в рамках Пеано. Среди них проблема Гольдбаха (4=2+2,6=3+3,8=3+5,…4=2+2,6=3+3,8=3+5,…), гипотеза Римана (о распределении простых чисел) или гипотеза Коллатца (последовательность 3n+13n+1).

Как писал сам Гёдель:

Математические истины не являются исключительно продуктом человеческого разума.

Культурные особенности подчеркивают, что ℕ — не универсальная данность. Так, римская запись (I, II, III) затрудняла вычисления в сравнении с вавилонской позиционной системой. Вавилонская 60-ричная система (остатки в делении часа на 60 минут) превзошла римскую благодаря позиционности: число (2×60 + 12 = 132) записывалось двумя клинописными символами. У аборигенов Австралии (племя гуугу йимитир) числа 1–5 совпадают с названиями частей руки: "большой палец"=1, "мизинец"=5, а 6–19 — комбинации ("мизинец другой руки"=6). Древние майя использовали 20-ричную систему: точка (•) = 1, черта (–) = 5, ракушка = 0; число записывалось как 3•20 + 5 = 65. В средневековой Европе римские цифры (I, V, X) делали деление почти невозможным — для расчётов использовали абак или пальцы, а математики писали трактаты словами ("трижды три — девять");

Философски натуральные числа являются фундаментом математики. Леопольд Кронекер утверждал, что

Бог создал натуральные числа, всё остальное — дело рук человека

Исторические заблуждения, вроде средневековой нумерологии (где числам приписывали мистическую силу), напоминают, что в XIX веке наука отделила математику от эзотерики.

1. Парадокс Гильберта, или Отель бесконечности

2. Гипотеза Римана, или Великая нерешённая задача

3. Гипотеза Коллатца, или проблема 3n+1

4. Проблема Варинга—Гольдбаха

5. Обобщённая гипотеза Ферма о полигональных числах

Сегодня ℕ лежат в основе RSA-шифрования (через простые числа) и теории алгоритмов, где они кодируют программы в машине Тьюринга.

Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.