Равновесие Нэша и дилемма заключенного: как математика связана с развитием человеческой цивилизации?3
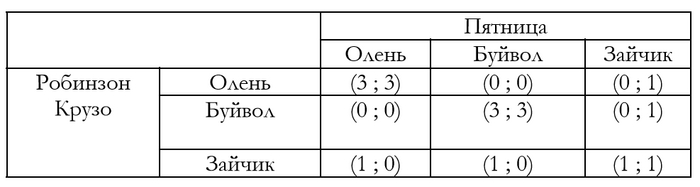
Равновесие Нэша [1] - это концепция из теории игр, которая объясняет, как в ситуациях с несколькими участниками каждый игрок может принимать решения, не желая менять свою стратегию, если остальные тоже остаются при своих. В равновесии Нэша все участники действуют оптимально относительно друг друга, даже если их действия не приводят к наилучшему личному результату [2].
Пример из фильма «Игры разума» помогает визуализировать эту идею. В одной из сцен Джон Нэш с друзьями сидит в баре, когда в помещение заходят несколько девушек, включая одну очень привлекательную блондинку. Друзья решают, что все должны попробовать привлечь внимание блондинки, ведь она самая красивая. Однако Нэш замечает, что если каждый будет пытаться ухаживать за блондинкой, они будут мешать друг другу, и в итоге никто не добьётся успеха — блондинка отвергнет всех, а остальные девушки почувствуют себя второстепенными и тоже откажут.
Тогда Нэш предлагает иную стратегию: никто из них не обращается к блондинке. Вместо этого каждый выбирает одну из её подруг. Это минимизирует конкуренцию и увеличивает шансы на успех, так как остальные девушки почувствуют себя ценными.
Вот этот отрывок из фильма, смотрите с 14 секунды, чтобы пропустить заставку канала:
Реальная математика за этой концепцией сложнее, но её можно представить как «баланс интересов», где каждый действует, учитывая действия других, и никому невыгодно действовать иначе. Хотя на самом деле принцип равновесия Нэша был известен человечеству уже более 19 столетий.
Равновесие Нэша и библейский принцип «возлюби ближнего своего, как самого себя» могут быть неожиданно связаны через идею гармоничного взаимодействия людей в обществе, где индивидуальные и коллективные интересы сбалансированы.
В равновесии Нэша каждый участник выбирает стратегию, которая оптимальна для него, учитывая действия других. Это не означает альтруизм, но предполагает, что участник осознаёт влияние своих действий на других. Если никто не может улучшить своё положение, не ухудшив положение остальных, достигается баланс. Принцип «возлюби ближнего своего, как самого себя» также олицетворяет баланс. Он призывает относиться к другим с такой же заботой, как к самому себе, не ставя свои интересы выше, но и не игнорируя их. Это создаёт основу для гармоничного сосуществования, где личные и общие блага взаимосвязаны.
В обоих случаях ключевой идеей является необходимость учитывать не только свои интересы, но и интересы окружающих. В равновесии Нэша это делается рационально, чтобы достичь устойчивого результата, а в библейском принципе - морально, чтобы построить справедливое общество. Если каждый будет действовать, думая и о себе, и о других (равновесие Нэша), либо любить ближнего, как себя (библейский принцип), то создаётся система, где меньше конфликтов и больше взаимной выгоды.
Представьте ситуацию, где несколько человек делят ограниченный ресурс, например, воду или еду. Принцип Нэша подскажет им найти баланс: никто не возьмёт больше, чем ему нужно, чтобы остальные не начали нарушать договорённости. Принцип любви к ближнему добавляет моральное измерение: люди добровольно ограничивают себя из заботы о других, возможно, даже жертвуя чем-то ради общего блага.
Фильм «Платформа» (2019) — это мощная метафора социального неравенства, идеально иллюстрирующая ситуации, где равновесие Нэша нарушается, а библейский принцип «возлюби ближнего своего, как самого себя» игнорируется. Башня представляет собой вертикальную тюрьму с множеством этажей. Ежедневно через башню движется платформа с едой, начиная с верхних этажей. Количество еды достаточно для всех, если бы её делили равномерно. Но на практике верхние уровни берут больше, чем им нужно, не оставляя ничего для нижних. Те, кто живут ниже, страдают от голода, злости и отчаяния.
В таком обществе каждый действует исходя из своих интересов, игнорируя последствия для других. На верхних этажах рационально предположить, что если ты не возьмёшь еду сейчас, то, оказавшись на нижних уровнях, можешь остаться без неё. Это приводит к тому, что каждый игрок берёт как можно больше еды, не думая о тех, кто ниже. Это стратегия индивидуального выживания, но она разрушает возможность устойчивого равновесия.
В результате система становится нестабильной: нижние этажи страдают, а высшие боятся, что в любой момент могут оказаться среди обделённых. Если бы узники следовали принципу «возлюби ближнего своего, как самого себя», они могли бы организовать равномерное распределение еды. Например, каждый мог бы взять ровно столько, сколько ему нужно. Это обеспечило бы выживание всех обитателей башни, стабилизировало систему и уменьшило бы насилие.
Почему система не достигает равновесия Нэша?
1) Недостаток доверия
Люди не верят, что другие придерживаются договорённостей, и предпочитают действовать эгоистично.
2) Отсутствие коммуникации
Узники изолированы и не могут договориться, что увеличивает хаос.
3) Принудительная система
Башня сама по себе стимулирует конкуренцию, а не сотрудничество.
«Платформа» показывает, как эгоистичное поведение разрушает общее благо. Чтобы выйти из замкнутого круга неравенства, необходимо больше, чем просто рациональный расчёт — нужна эмпатия, доверие и готовность делиться ресурсами. Это напоминает, что для устойчивости общества важно сочетать рациональность (равновесие Нэша) и моральные принципы.
Дилемма заключенного
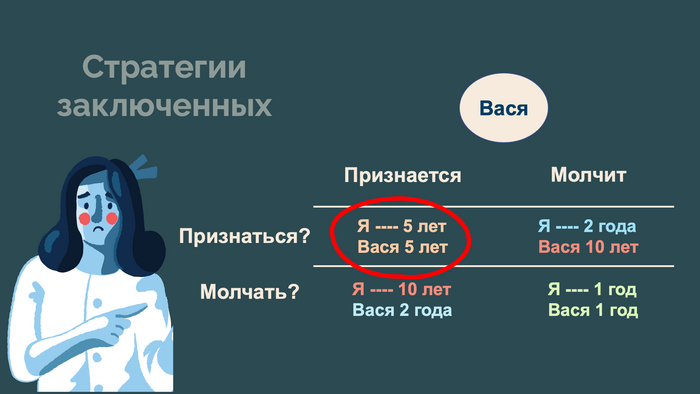
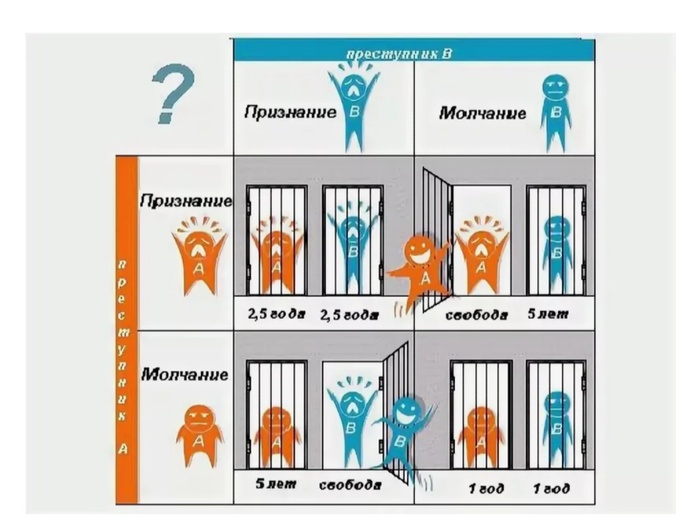
Дилемма заключённого [3] - это классический пример из теории игр, который прекрасно иллюстрирует проблему недостатка доверия и его влияние на принятие решений. Она показывает, как рациональное поведение в условиях недоверия может привести к худшему исходу для всех участников.
Два подозреваемых арестованы и изолированы друг от друга. Им предложены варианты:
1) Если один сдаёт другого (предательство), а второй молчит, предатель освобождается, а молчащий получает максимальный срок (например, пожизненное заключение).
2) Если оба молчат, они получают минимальный срок (например, 1 год).
3) Если оба предают, они оба получают средний срок (например, 5 лет).
Поскольку игроки не могут доверять друг другу, логично предположить, что другой выберет предательство, чтобы минимизировать свой срок. Поэтому оба обычно выбирают предательство, что приводит к среднему сроку для каждого, хотя если бы они доверяли друг другу и молчали, их срок был бы минимальным.
В дилемме заключенного участники не могут договориться или гарантировать выполнение соглашения, поэтому действуют из страха быть обманутыми. Каждый участник пытается защитить себя от максимального наказания, что приводит к взаимному предательству. В условиях недоверия участники ориентируются только на свои интересы, не принимая во внимание возможные преимущества совместных действий.
Пример фильма «Платформа» показывает, что еда распределяется аналогично дилемме заключённого:
1) Если верхние этажи «молчат» (берут только свою долю), еды хватит всем.
2) Если они «предают» (берут больше, чем нужно), нижние этажи страдают.
Из-за недостатка доверия (верхние этажи предполагают, что если они не возьмут больше, кто-то другой с их этажа это сделает) система разваливается. Взаимное недоверие ведёт к хаосу, где каждый действует эгоистично.
Как преодолеть недостаток доверия?
1) Коммуникация
Если участники смогут договориться, шансы на кооперацию возрастут.
2) Внешние правила
Вмешательство третьей стороны (например, строгие законы или контроль) может стабилизировать систему.
3) Долгосрочные отношения
В повторяющихся играх участники склонны сотрудничать, так как понимают, что их действия влияют на будущее взаимодействие.
Дилемма заключённого и её связь с недоверием - это универсальная модель, применимая в реальной жизни: от социальных конфликтов до экономических систем. Она учит, что для достижения наилучшего коллективного результата необходимы не только рациональность, но и готовность к доверию и сотрудничеству.
Общественный строй и математика
Сравнение капитализма и коммунизма через призму равновесия Нэша и дилеммы заключённого позволяет выявить их сильные и слабые стороны в контексте кооперации, доверия и эффективности решения социальных проблем.
Капитализм поощряет каждого участника системы (предприятия, работников, потребителей) действовать в своих собственных интересах. Это часто приводит к ситуации, где каждый принимает оптимальное решение для себя, но не всегда для общества. Конкуренция стимулирует инновации и развитие, но приводит к неравномерному распределению ресурсов (например, богатство концентрируется у элит).
Капитализм создаёт множество ситуаций, где компании или люди принимают решения, основанные на недоверии. Например, загрязнение окружающей среды выгодно для отдельных корпораций, даже если оно наносит ущерб обществу. Недостаток кооперации и ориентация на краткосрочную выгоду затрудняют решение глобальных проблем, таких как изменение климата или социальное неравенство.
Коммунизм стремится к тому, чтобы участники действовали в интересах всего общества. В идеальной коммунистической системе люди выбирают стратегии, которые максимизируют общественное благо. Таким образом, коммунизм приводит к равновесию, где ресурсы распределяются справедливо, что снижает социальное напряжение.
Коммунизм предполагает высокую степень доверия между участниками системы. Если кто-то начинает действовать эгоистично (например, злоупотреблять ресурсами), система становится нестабильной. Исторически попытки реализации коммунизма сталкивались с проблемой морального риска: когда люди считают, что могут получать выгоды, не внося вклад, доверие разрушается.
Какой строй более выгоден для цивилизации?
Идеальный ответ может лежать в синтезе лучших черт обеих систем:
1) Кооперативный капитализм - модель, в которой рыночная конкуренция сочетается с сильными социальными гарантиями и глобальным сотрудничеством для решения общих проблем.
2) Технологический коммунизм - система, где технологии (например, искусственный интеллект и автоматизация) устраняют необходимость жёсткой иерархии, позволяя справедливо распределять ресурсы.
Капитализм быстрее продвигает технологии из-за конкуренции. Коммунизм эффективнее в устранении социальных неравенств, что ускоряет развитие человеческого потенциала в долгосрочной перспективе. Капитализм решает проблемы выборочно, ориентируясь на прибыль. Коммунизм направлен на системное решение проблем, но часто сталкивается с трудностями в реализации. Для устойчивого развития цивилизации в долгосрочной перспективе потребуется гибридная модель, объединяющая технологический прогресс капитализма с кооперативными и справедливыми принципами коммунизма. Это позволит эффективно решать социальные проблемы и одновременно сохранять высокий темп инноваций.
Литература
[1] Nash, John F. (1950) Equilibrium points in n-person games // PNAS. 36 (1): 48–49. doi:10.1073/pnas.36.1.48
[2] Мазалов В. В. Математическая теория игр и приложения. — Изд-во Лань, 2010, 446 с.
[3] Poundstone, William (1992) Prisoner’s Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb. — Doubleday. ISBN 0-385-41567-2.