Аритмомахия (пункт 1, натуральные числа)
Математика, во всем своём невероятном разнообразии, от криптографии и искусственного интеллекта до теоретической физики и финансовых моделей, опирается на универсальный язык. И этот язык числа. Однако сами числа не монолитная сущность. Они существуют в стройной иерархии взаимосвязанных систем, каждая из которых возникла как ответ на фундаментальные вопросы и ограничения предыдущей.
Примечание: ℕ, ℤ, ℚ, ℝ и ℂ— стандартные символы Юникода (exempli gratia, ℕ = U+2115), предназначенные специально для множества натуральных, целых, рациональных, вещественных и комплексных чисел соответственно. Использование данных символов исключает двусмысленность, вроде "...пусть N — натуральное число, тогда N ∈ N", что только запутает читателя.
В этом цикле статей мы совершим путешествие по удивительным мирам чисел: от простых и интуитивных натуральных чисел (ℕ), служащих для счета дискретных объектов, до загадочных комплексных чисел (ℂ), описывающих волновые процессы в квантовой механике и электротехнике.
Понимание этой иерархии, ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ, не просто академическое упражнение. Это ключ к осознанию того, почему математика работает так эффективно для описания мира. Мы увидим, как дискретность ℕ и ℤ управляет логикой вычислений, как непрерывность ℝ описывает физические законы движения и изменения, и как двумерность ℂ кодирует информацию о фазе и амплитуде в волновых процессах.
Готовы отправиться в путешествие от камешков до квантовых волн?
Начнем с самого основания, мира натуральных чисел (ℕ).
История натуральных чисел началась с практических потребностей древних цивилизаций. Зарубки на костях Ишанго, сделанные около 20 000 лет до н.э., свидетельствуют о первых попытках счета скота, урожая или дней. Шумеры (IV тысячелетие до н.э.) использовали числа для учета зерна, скота и налогов, а вавилоняне применяли их в астрономических расчетах движения планет уже во II тысячелетии до н.э.
Вавилоняне использовали пробел для обозначения нуля в записи чисел (напр., 1‿3 для 103), но не признавали его самостоятельной сущностью.
Эти числа, 1, 2, 3 и далее, стали фундаментом математики, и ноль долгое время не входил в их состав. Но отсутствие нуля было лишь частью решения более сложных задач.
Вавилоняне и майя использовали ноль как позиционный символ, но не считали его числом. В Европе ноль признали лишь в XII веке благодаря трудам Аль-Хорезми, хотя Аристотель отвергал его, утверждая, что
...природа не терпит пустоты.
К вопросу о нуле мы ещё вернёмся в следующих статьях.
Натуральные числа не могли решить уравнения типа x+3=1x+3=1 или корректно выразить результат деления 5 на 3, что позже привело к созданию целых и рациональных чисел. Античные философы, такие как Зенон, оспаривали саму возможность бесконечности ℕ, а средневековые теологи спорили, может ли Бог создать "наибольшее натуральное число".
Формализация ℕ завершилась в XIX веке. Пифагорейцы (V в. до н.э.) пытались свести мир к целым числам, но открытие иррациональности √2 разрушило эту идею.
Пифагорейцы обнаружили, что даже задача измерения диагонали квадрата (√2) неразрешима в рамках ℕ и их дробных отношений — это стал первый кризис оснований математики.
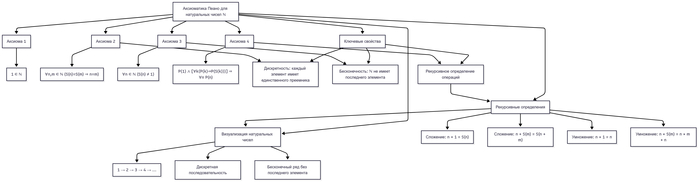
В 1889 году Джузеппе Пеано создал строгую аксиоматику:
1. 1 ∈ ℕ;
2. ∀n,m∈N(S(n)=S(m)⇒n=m) (инъективность функции следования, т. е. каждое число имеет последующее);
3. ∀n∈NS(n)≠1 (непредикативность 1, т. е. 1 не следует ни за каким числом);
4. [P(1) ∧ ∀k (P(k)⇒P(S(k)))]⇒∀n P(n) (принцип математической индукции, т. е. равенство последующих элементов влечет равенство самих чисел);
Аксиоматика Пеано (в вариантах с 0 или 1) остаётся стандартом.
Теоремы Курта Гёделя навсегда изменили наше понимание математики, показав принципиальные ограничения формальных систем. Применительно к натуральным числам их суть такова: любая достаточно мощная и непротиворечивая система аксиом (включая аксиомы Пеано) неспособна полностью охватить все истинные свойства натуральных чисел.
Это означает, что всегда существуют утверждения, которые истинны с содержательной точки зрения, но формально недоказуемы в рамках самой системы — и их отрицание также недоказуемо.
"Машина Тьюринга с номером n не останавливается на пустом вводе".
Это утверждение истинно для некоторых n (если машина действительно не останавливается) и недоказуемо в аксиомах Пеано. Такие утверждения относятся к конкретным свойствам натуральных чисел (номерам алгоритмов).2. Натуральные числа обладают интуитивно ясными свойствами: бесконечность ряда 1,2,3,…1,2,3,…, корректность рекурсивных определений (сложение, умножение). Но никакая формальная система не может полностью захватить эту интуицию. Всегда останутся истины, невыводимые из аксиом.
3. Гипотезы в теории чисел могут быть принципиально недоказуемыми в рамках Пеано. Среди них проблема Гольдбаха (4=2+2,6=3+3,8=3+5,…4=2+2,6=3+3,8=3+5,…), гипотеза Римана (о распределении простых чисел) или гипотеза Коллатца (последовательность 3n+13n+1).
Как писал сам Гёдель:
Математические истины не являются исключительно продуктом человеческого разума.
Культурные особенности подчеркивают, что ℕ — не универсальная данность. Так, римская запись (I, II, III) затрудняла вычисления в сравнении с вавилонской позиционной системой. Вавилонская 60-ричная система (остатки в делении часа на 60 минут) превзошла римскую благодаря позиционности: число (2×60 + 12 = 132) записывалось двумя клинописными символами. У аборигенов Австралии (племя гуугу йимитир) числа 1–5 совпадают с названиями частей руки: "большой палец"=1, "мизинец"=5, а 6–19 — комбинации ("мизинец другой руки"=6). Древние майя использовали 20-ричную систему: точка (•) = 1, черта (–) = 5, ракушка = 0; число записывалось как 3•20 + 5 = 65. В средневековой Европе римские цифры (I, V, X) делали деление почти невозможным — для расчётов использовали абак или пальцы, а математики писали трактаты словами ("трижды три — девять");
У племени пираха́ (Амазония) отсутствуют числительные >2 ("много") — это подтверждает гипотезу лингвиста Бенджамина Уорфа: язык формирует математическую реальность.
Философски натуральные числа являются фундаментом математики. Леопольд Кронекер утверждал, что
Бог создал натуральные числа, всё остальное — дело рук человека
Исторические заблуждения, вроде средневековой нумерологии (где числам приписывали мистическую силу), напоминают, что в XIX веке наука отделила математику от эзотерики.
1. Парадокс Гильберта, или Отель бесконечности
Представьте отель с бесконечными номерами (ℕ), где все места заняты. Приезжает новый гость. Можно ли его разместить? Да, если попросить каждого гостя переселиться в соседний номер: гость 1 → 2, 2 → 3, и так далее. Освободившийся номер 1 отдают новичку. Так доказывается, что ℕ + 1 = ℕ. Парадокс иллюстрирует свойство бесконечных множеств: их часть может быть равна целому.
2. Гипотеза Римана, или Великая нерешённая задача
Все "нетривиальные нули" дзета-функции Римана (специальной функции, связанной с простыми числами) лежат на одной волшебной линии — "критической прямой" Re = 1/2. Простые числа (2,3,5,7...) распределены в ℕ хаотично. Бернхард Риман связал их с дзета-функцией. Если гипотеза верна, простые числа (2,3,5,7...) распределены не хаотично, а подчиняются скрытому порядку. Задача входит в список "Проблем тысячелетия" с премией $1 млн.
3. Гипотеза Коллатца, или проблема 3n+1
Если n чётное, разделите его на 2: n/2n/2.Если n нечётное, примените 3n+13n+1.Независимо от начального n, последовательность всегда достигнет 1. Открыта с 1937 года. Проверена для всех n<268n<268, но общее доказательство отсутствует. Пример: для n=27n=27 последовательность требует 111 шагов до достижения 1.
4. Проблема Варинга—Гольдбаха
Верно ли, что для любого натурального n>1n>1 и достаточно большого k, каждое достаточно большое натуральное число NN представимо в виде: N=p1n+p2n+⋯+pkn,N=p1n+p2n+⋯+pkn, где pipi — простые числа?
Проблема обобщает проблему Гольдбаха (сумма простых) и проблему Варинга (сумма степеней). Для n=1n=1 и k=3k=3 эквивалентна тернарной проблеме Гольдбаха (доказана Виноградовым в 1937 г.). Для n≥2n≥2 остаётся открытой.
5. Обобщённая гипотеза Ферма о полигональных числах
Любое натуральное число ℕ может быть представлено в виде суммы не более mm mm-угольных чисел. Треугольные числа: Tk=k(k+1)2Tk=2k(k+1) (например, 1, 3, 6).
Квадратные числа: Kk=k2Kk=k2 (например, 1, 4, 9). Для любого m≥3m≥3 существует число g(m)g(m), такое что каждое NN выражается суммой g(m)g(m) mm-угольных чисел. Для квадратов (m=4m=4): g(4)=4g(4)=4 (теорема Лагранжа, 1770 г.).
Для треугольников (m=3m=3): Гаусс доказал, что g(3)=3g(3)=3 (1796 г.).
Доказан Гильбертом в 1909 г., но точные значения g(m)g(m) известны лишь для некоторых mm (например, g(5)=5g(5)=5, g(6)=6g(6)=6).
Сегодня ℕ лежат в основе RSA-шифрования (через простые числа) и теории алгоритмов, где они кодируют программы в машине Тьюринга.
Наш главный приоритет - публикация качественного и достоверного материала. Каждая статья проходит многоэтапную проверку нашей командой.
Важно: материалы нашего проекта носят исключительно информативный характер. Они не являются образовательным контентом и не заменяют академические источники.