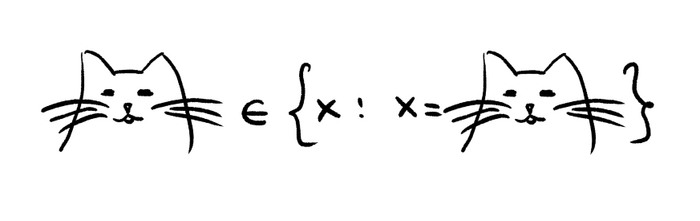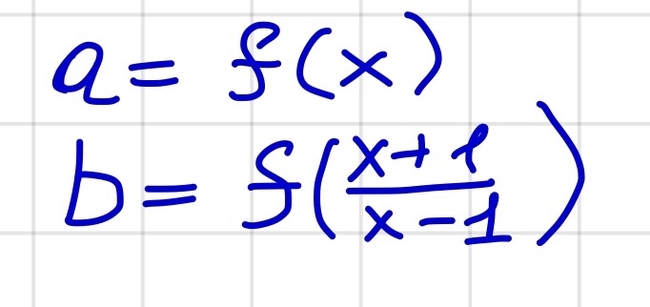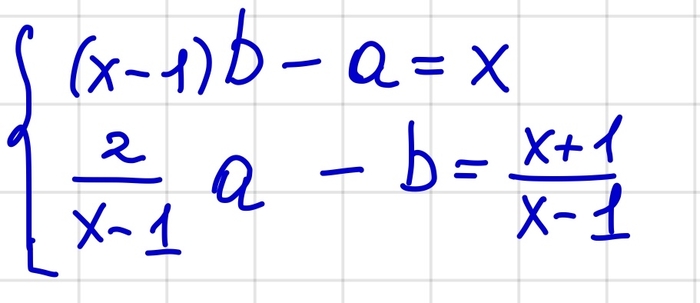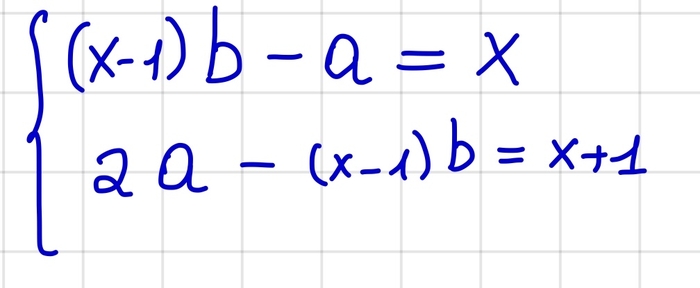Бесконечный рассказ о бесконечности. Часть вторая -- бесконечность не предел!
Всем привет! В прошлом посте я обсуждал понятие бесконечности в математике. Задача на сегодня -- понять этот мем (и не только):
В прошлый раз мы получили два результата:
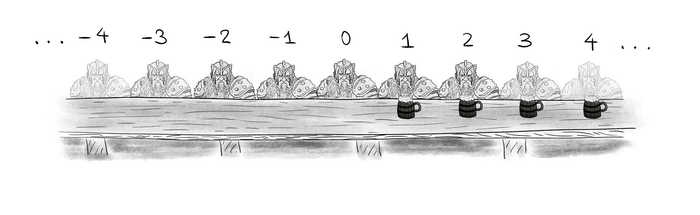
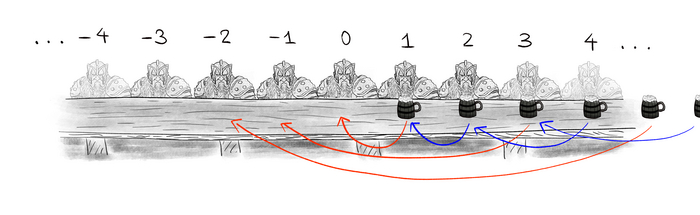
Во-первых мы выяснили, что даже если одна бесконечность в бесконечное количество раз больше другой, может оказаться, что на самом деле в ней "столько же" элементов, что и в изначальной (тот пример с армией гномов и пивом).
Во-вторых, оказалось, что бывают гораздо большие бесконечности, в которых всё-таки строго больше элементов, чем в "счётной" бесконечности (т.е. той, где все элементы можно перенумеровать с помощью натуральных чисел). Например, мы выяснили, что множество вещественных чисел из интервала (0,1) мы перенумеровать никак не можем и назвали такую бесконечность континуумом.
Сегодня я бы хотел немного поиграть с бесконечностями и порассуждать о том, есть ли что-то большее, при каких операциях что получается и так далее. Да, кстати, если у вас будут возникать вопросы или желание что-нибудь обсудить другое -- пишите в комментах, я почти всегда тут.
План на сегодня
1. Понятие равномощности, примеры
2. Мощность множества подмножеств
3. Гипотеза континуума (в двух словах)
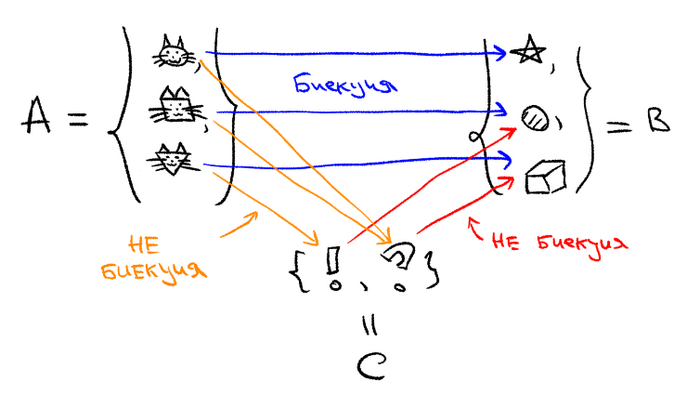
Итак, начнём. В этом посте я буду много оперировать с множествами (про понятие множества я писал пост, но вкратце можно рассматривать их как просто наборы, совокупности каких-то элементов). Допустим у нас есть два множества -- A и B. Что означает, что у них одинаковое количество элементов? Допустим, что у нас получилось разбить элементы множества А и элементы множества B на пары, т.е. мы каким-то образом нашли для каждого элемента множества А, единственный элемент множества B, так, чтобы во-первых, разным элементам из A соответствовали разные из B, а во-вторых любой элемент из B оказался в паре с кем-то (т.е. мы никого не забыли из B). Я люблю представлять себе это на картинках, пример (классический) -- у нас есть отель и в него заселяются люди по одному на комнату. Мы говорим, что комнат в отеле столько же сколько же сколько и людей, если каждого человеку мы заселяем в комнату так, чтобы никакие два человека не жили вместе, и никакая комната не осталась пустой. (Ну или можете такую же аналогию сделать для гномов из предыдущего поста). Если у нас получилось сделать такое соответствие, мы будем называть его биекцией. Множества, между которыми биекция существует, мы будем называть равномощными.
(Рыжее отображение не биекция, т.к. двум разным котам достался один и тот же знак. Красное отображение не биекция, потому что пятиконечной звезде никто не достался)
В прошлом посте мы доказали, что множество натуральных чисел (ℕ) равномощно множеству целых чисел (ℤ), и оно же равномощно множеству пар из целых чисел (ℤ×ℤ -- декартов квадрат целых чисел). Вот ещё два быстрых примера равномощных множеств:
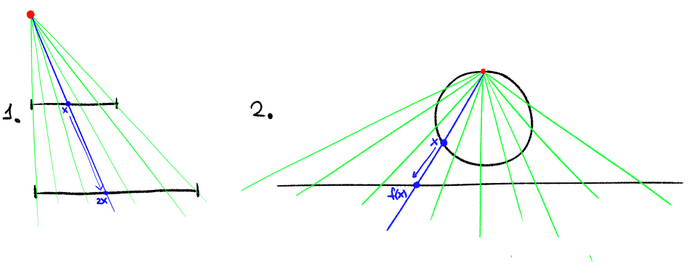
1. Отрезок [0,1] равномощен отрезку [0,2] (биекция осуществляется функцией f(x) = 2x)
2. Пусть A = окружность без точки а B -- все вещественные числа (ℝ). Тогда A равномощно B (биекция f(x) -- стереографическая проекция, см. рисунок)
(Представьте себе, что в красной точке светит лампочка и вы каждой точке верхнего множества сопоставляете её тень на нижнем множестве).
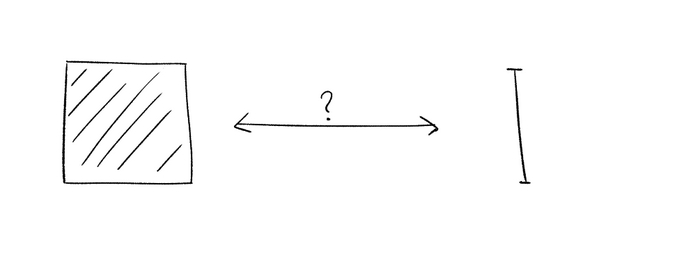
Во всех примерах которые у нас уже были биекции строились одним из двух способов -- для счётных множеств мы просто явно перенумеровывали множество, а для отрезков/прямых мы непрерывно растягивали множества (т.е. пример 1. был просто масштабированием, а в пример с окружностью без верхней точки мы просто растянули ее в бесконечность). Бывают более хитрые случаи. Давайте докажем, что двумерный квадрат (со всеми внутренними точками) равномощен отрезку.
(этот квадрат озадачен предложением поместиться в отрезок)
Честно говоря мне на этом моменте в своё время было вообще не понятно как такое может быть -- действительно, точек в квадрате не просто в бесконечное количество раз больше, чем в отрезке, а в "очень большое бесконечное" раз (т.е. квадрат состоит из континуума отрезков). Однако есть финт, который это позволяет достаточно просто доказать. Я докажу версию где мы берём множество внутренних точек квадрата (т.е. без границы) и множество внутренних точек отрезка (т.е. интервал), версия с границами доказывается примерно так же, ну или с помощью другого трюка, который говорит, что если множество А вложено в B и B вложено в C и A равномощно C, то и все они равномощны B (это один из вариантов теоремы Кантора-Берштейна, доказывается очень красиво, однажды расскажу)
Каждая точка в квадрате представима в виде пары координат (x,y), где x и y -- вещественные числа (из интервала (0;1)). Давайте представим каждое из них в виде бесконечной десятичной дроби:
x = 0,x₁x₂x₃x₄...
y = 0,y₁y₂y₃y₄...
(напишите мне если едут символы, но вроде бы юникод, должно быть норм)
Теперь мы построим из этих двух чисел одно число следующим образом -- будем чередовать цифры из первого числа и второго. Т.е. полученное число будет выглядеть так:
z = 0,x₁y₁x₂y₂x₃y₃x₄y₄...
Очевидно оно из интервала (0,1). Более того, очевидно, что никакие две разные пары (x,y) и (x',y') не могли дать одинаковое число. Для того чтобы доказать, что мы заполнили все числа из интервала, достаточно заметить, что любому числу z=0,z₁z₂z₃z₄... соответствует пара (0,z₁z₃..., 0,z₂z₄...). Значит мы получили биекцию!
Данный пример отличается от предыдущих тем, что он очень сильно НЕ непрерывен, т.е. точки при таком отображении будут очень сильно "разрывать квадрат". Но тем не менее оказалось что число точек интервала такое же, как и внутренности квадрата.
Вообще для любого множества X мы можем построить так называемый декартов квадрат X×X, элементы которого это все возможные пары (x, x'), где x, x' из X (X×X = { (x, x') : x, x' ∈ X}). Мы уже доказали что декартов квадрат целых чисел равномощен целым числам и декартов квадрат интервала (0,1) равномощен самому интервалу. Возникает вопрос -- а верно ли то, что для любого бесконечного множества X оно равномощно своему декартовому квадрату? Оказывается да, но для доказательства этого требуется определённая приём (а именно лемма Цорна), о котором я расскажу в одном из следующих постов.
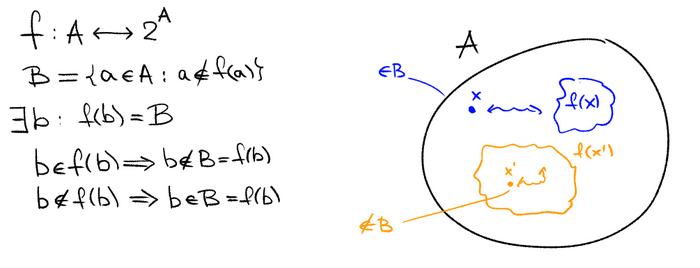
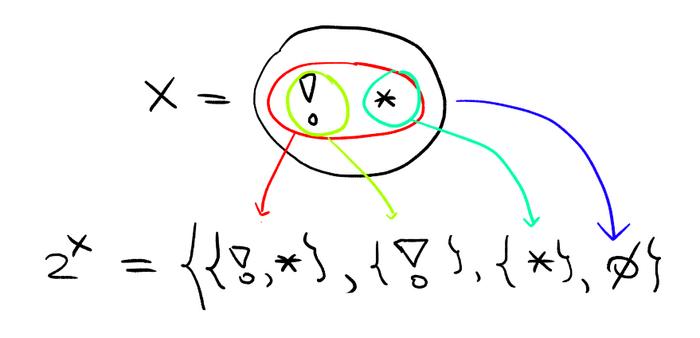
Итак, у нас есть счётные множества, есть континуальные множества. Есть ли что-то большее? Ответ -- да, причём бесконечно много! Для того, чтобы это доказать, рассмотрим любое множество A и множество всех его подмножеств (включая само A и пустое подмножество) -- 2ᴬ. Такое обозначение выбрано потому, что если множество A конечное и состоит из n элементов, то у него как раз ровно 2ⁿ подмножеств (это следует из того, что каждый из элементов мы можем либо взять, либо не взять для того, чтобы построить подмножество). Давайте докажем, что А не равномощно 2ᴬ. Допустим существует биекция f из A в 2ᴬ. Значит каждому элементу a ∈ A соответствует подмножество f(a) ⊂ А. У нас есть два варианта -- либо a ∈ f(a), либо нет. Соберем все такие элементы, которым не повезло попасть в свой образ в множество B, т.е. B = { a ∈ A : a ∉ f(a) }. Очевидно это подмножество A (B ⊂ A). Но у нас f -- это биекция, т.е. существует какой-то элемент, который соответствует этому подмножеству (т.е. есть элемент b∈ A: f(b)=B). Вопрос -- а верно ли, что b∈B? (у тех кто читал пост про множества должны возникнуть смутные сомнения...)
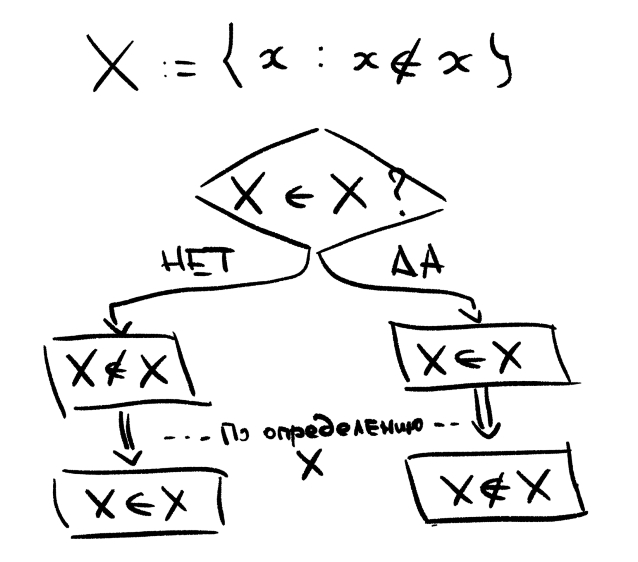
Допустим да, это верно, т.е. b∈B. Но по определению B в него попадают только те элементы, которые не попадают в свой образ, а при этом b∈f(b)=B. Значит так быть не может, т.е. b ∉ B.
Получается что b ∉ B. Но тогда, опять же по определению B, b должен попасть в свой образ (потому что всё, что не попадает ушло в B). Значит b∈f(b)=B, т.е. b∈B. Как такое может быть? Никак, поэтому противоречие! Значит такой биекции не существует!
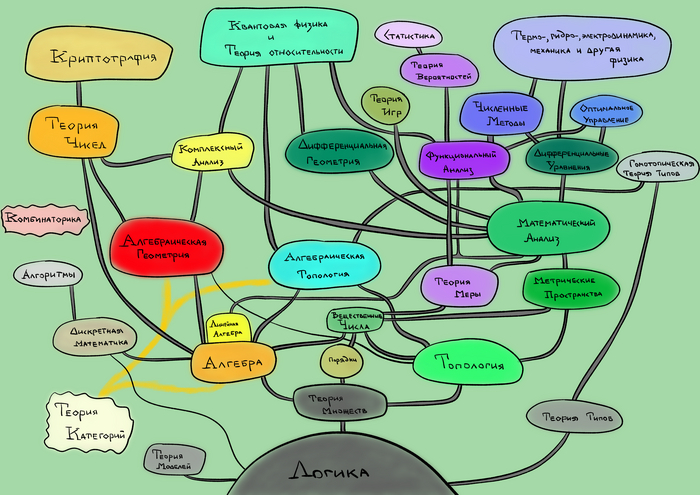
(Поясняющая картинка, а то понимать свой текст мне самому уже сложно)
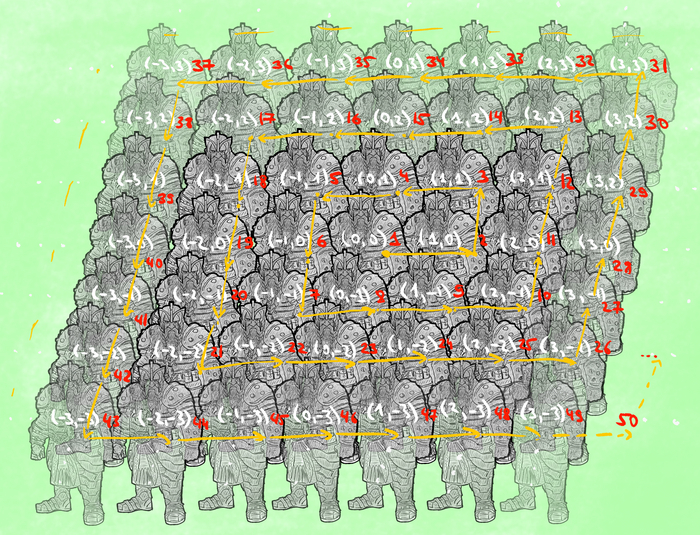
При этом очевидно, что в 2ᴬ больше элементов чем в А -- действительно, мы можем вложить А просто как одноэлементные подмножества -- a -> {a} ⊂ A. Получается, что в 2ᴬ элементов в очень большое количество раз больше элементов для любого множества A. А что это означает? Мы можем делать такую процедуру итеративно, т.е. взять множество всех подмножеств 2ᴬ, множество всех подмножеств всех подмножеств 2ᴬ и т.д. -- получим такую бесконечную цепочку разных бесконечностей. Мало того, далее вы можете объединить все что вы придумали -- получится ещё большее множество! И так далее -- каждый раз вы берете множество всех подмножеств, а если вы сделали это бесконечное число раз -- объединяете все. Ежели и это действие вы сделали бесконечное число раз -- вы снова объединяете! Выглядит это примерно все так:
(кстати омега-в-степени-омега-в-степени-омега-... и так омега раз иногда обозначается ε₀)
Вы спросите -- а что это за число такое -- омега (а так же омега в квадрате, омега в степени омега...). Это -- некоторый способ научиться считать бесконечности, называемый ординалами (как их строить и что это такое мы однажды обсудим). Важно, что вообще говоря таких ординалов намного больше, чем можно сосчитать с помощью этих омег, но для начала и такое представление сойдёт.
Мы научились получать бесконечное число разных бесконечностей (тут я неявно говорю "бесконечных множеств разной мощности")! Мы сейчас это сделали, строя следующее бесконечное множество с помощью того, что брали множество всех его подмножеств. Как мы уже знаем, следующее множество "строго больше" предыдущего. Но вот вопрос -- "перечислили" ли мы таким образом все бесконечности (если например бы мы начали с натуральных чисел). Если нет, то как вообще устроена эта система бесконечностей?
Для начала, отвечу на второй вопрос: можно доказать, что система мощностей устроена примерно таким же образом, как и то, что мы строили. Иначе говоря, первая бесконечность -- это счётная. Такая бесконечность обозначается символом ℵ₀ (алеф-0). Далее, доказывается, что существует минимальная бесконечность которая больше счётной -- мы называем её "алеф-1" -- ℵ₁. За ней следует ℵ₂, ℵ₃, ... . Точно так же как и в случае до этого, появляется ℵ-омега, ℵ-омега-в-квадрате и т.д. (в юникоде нет сабскрипта омеги : ( ). И теперь точно можно утверждать, что любое множество имеет мощность одну из алефов.
Терминология -- все эти числа, выражающие мощность множества называются кардинальными числами). Каждому множеству таким образом сопоставляется кардинальное число и два множества равномощны тогда и только тогда, когда их кардинальные числа равны (не путайте кардиналы и ординалы -- первые выражают мощности, а вторые -- это просто некоторый способ занумеровать бесконечную число элементов. В частности ординалы нумеруют всевозможные кардинальные числа). Кстати говоря, я совсем забыл про конечные множества (кому они нужны, да?) -- для них мощность -- это просто число элементов, а соответствующие кардинальные числа -- просто натуральные.
Теперь ответ на второй вопрос -- а не пропустили ли мы чего-нибудь? Этот вопрос можно сформулировать ещё так -- верно ли что если бесконечно множество А имеет кардинальное число ℵₖ, то 2ᴬ будет именно следующим бесконечным множеством, т.е. иметь кардинальное число ℵₖ₊₁? Вот оказывается, что в рамках наших аксиом (т.е. стандартной системы аксиом теории множеств -- аксиом Цермелло-Френкеля (с или без аксиомы выбора)) такое утверждение нельзя ни доказать, ни опровергнуть! Т.е. что бы вы не предположили, вы никогда не получите противоречия. На мой взгляд это удивительный утвреждение, называемый обобщенной континуум-гипотезой. Кстати, забавный факт -- не смотря на то, что эта гипотеза не доказуема и не опровергаема, если её принять за аксиому, то из неё будет следовать одна из других аксиом теории множеств -- так называемая аксиома выбора (о которой мы поговорим позже).
В частности, изначально эта проблема начиналась с самых маленьких бесконечностей: давайте возьмём наименьшую бесконечность ℵ₀ -- мощность множества натуральных чисел. Мы знаем что множество подмножеств натуральных чисел равномощно множеству точек на интервале, т.е. имеет мощность континуум (доказывается примерно так: надо воспользоваться двоичной системой и сопоставить каждому подмножеству бесконечную последовательность из нулей и единиц. Дальше этой последовательности мы сопоставляем число в двоичной записи. Проблема тут в том, что некоторые последовательности так "склеиваются" в одно и то же число. Но к счастью это не влияет на мощность, т.к. таких плохих случаев "всего лишь" счётное число). Но вопрос -- верно ли, что континуум это первая бесконечность после счётной? Это утверждение уже называется просто -- континуум гипотеза. И точно так же, как и обобщённая, она может быть верна, может быть не верна, и в обоих случаях не возникнет никаких противоречий!
Уф, вот такая вот математика. В следующий раз мы обсудим немного аксиому выбора и, пользуясь ею, будем делить апельсины!