Это продолжение серии про "опережающую" математику в школах США, начавшуюся вводной статьёй Опережающая математика в школах США. 0 - Введение
Как уже было написано раньше, матанализ не относится к обязательным школьным предметам в США. Он широко распространён, но изучать его - не норма. Примерно шестая часть нынешних выпускников американских школ проходила матанализ.
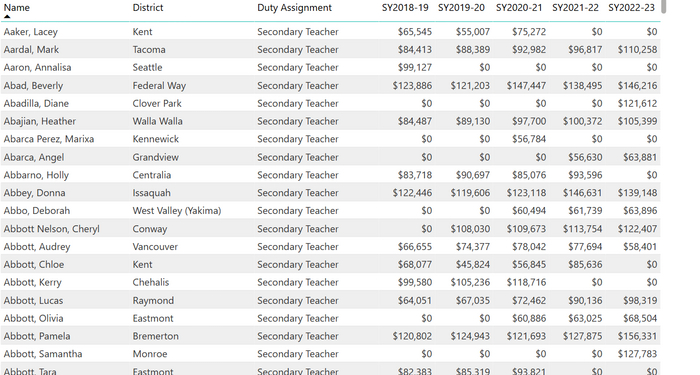
В позапрошлом году около 410 тысяч учеников пытались сдать экзамен AP Calculus (AB или BC), выпускников же каждый год около 3,8 млн. Из сдававших только 65% получили положительную оценку. Эта статистика не полностью отражает реальную картиру: часть студентов пересдавали прошлогодний провал, часть сдающих BC уже раньше сдавали AB, то есть всего AP-экзамен по матанализу сдавали больше 300, но меньше 400 тысяч учеников. Редкие школьники сдавали экзамен, не проходив курс в школе (занимаясь самостоятельно, на курсах или у себя на родине). С другой стороны, часть ребят курс матанализа прошли, но экзамен не сдавали: заболели, испугались, пожмотились (экзамены платные), поленились. На небольшой выборке было оценено, что примерно каждый четвёртый-пятый, проходивший курс AP Calculus, экзамен не пишет, а около 2% тех, кто не проходил курс, пошёл на экзамен. Некоторые проходили иной курс матанализа и сочли, что их курс круче, например спецпредмет в частной школе или IB Mathematics Analysis and Approaches. И всё-таки AP Calculus - самый массовый из американских матанализов, он появился еще в 1956 году одновременно со всей системой экзаменов и курсов Advanced Placement. Так что будем ориентироваться на него.
Основы матана, как и другие курсы, в США проходят как правило каждый учебный день, то есть около 180-190 дней по 50-60 минут. И идут туда не все. Стандартный набор математических курсов заканчивается в 12 классе "преданализом", о котором я, возможно, напишу в одной из следующих статей. Чтобы попасть на матанализ, ученик должен как минимум опережать стандартную программу минимум на год. Вероятно, из предыдущего курса он уже имеет представление о пределе (но, в отличие от русских школьников, не имеет представление о производных, - в России к ним готовят уже в 9 классе на физике). Также ученик должен сам пожелать изучать этот предмет: обычно в 12 классе проходить математику не обязательно, и вместо матана можно выбрать математические курсы попроще типа статистики или бизнес-матана. Так что имеем взрослых отборных энтузиастов, занимающихся матаном что-то около 170 астрономических часов в классе, не считая домашек.
Неудивительно, что американский школьный матан гораздо сильнее российского. Как уже сказано в предыдущей статье, для желающих и способных учеников отставание от РФ в средних классах сменяется стремительным опережением в последних классах. В итоге американские отличники не умеют решать алгебраические уравнения, обычные для российских хорошистов, зато заткнут за пояс большинство российских выпускников в матанализе.
Итак, что же проходят американцы в курсе AP Calculus? Курса два: AP Calculus AB и AP Calculus BC. Второй включает всё то же, что первый, и еще немного. Кстати, поэтому для изучавших "сложный" курс BC экзамен по BC оказывается проще, чем по AB: времени на экзаменах выделяется одинаково, задач сравнимое количество, но из-за более широкой программы BC на экзамене даются более простые задачи из подмножества AB. Это, а также то, что курс BC проходят обычно более способные и целеустремлённые ребята (а иногда его сдают те, кто изучал матан целых два года), процент успешно сдавших сложный BC гораздо выше, чем простой AB: 78% со средним баллом 3,75 против 58% со средним баллом ниже 3,0.
Темы, изучаемые в предмете AP Calculus AB:
графики. Это сравнительно сложная тема, типичная задача - учитель от руки рисует какие-то несимметричные гладкие немонотонные функции 𝑓(𝑥) и 𝑔(𝑥) и просит нарисовать композицию 𝑓(𝑔(𝑥))
пределы функций (по Коши), непрерывность
производные, вывод производных элементарных функций, сложных, неявных, обратных, производные высших порядков
аппроксимации, правило Лопиталя, теорема о среднем значении
анализ функций с помощью производных, решение оптимизационных задач, неявные зависимости
определённый интеграл через суммы Римана, первообразная и неопределенный интеграл, теорема Ньютона-Лейбница
приёмы интегрирования, практические задачи на интегрирование
решение дифференциальных уравнений методом разделения переменных на несложных примерах
В предмете AP Calculus BC проходят то же самое и вдобавок:
больше приёмов интегрирования
решение дифуров численным методом Эйлера
движение вдоль гладкой кривой
производные в параметрических уравнених, полярных координатах, векторных функциях
последовательности и ряды, определение области сходимости, разложение в ряд Тейлора, оценка остаточного члена
На мой взгляд, это глупо: разложение в ряд Тейлора - чуть ли не основной результат матана, и его стоило изучать на любом уровне сложности. Тем более что американские школьники и большинство студентов не проходит действительные числа, так что о строгости всего матана говорить не приходится. Настоящий матан (Real Analysis) проходят обычно на третьем курсе вуза те студенты, кто выбрал математику своей специальностью.
Сравним американский школьный матан (кстати, он обычно и в вузе засчитывается как предмет 1 курса, даже для будущих математиков) с российским. В российской школьной программе изучается или изучалось:
действительные числа (на пальцах)
последовательности - введены в школу в 1960-х (программа Кочеткова), убраны в 1970-х (программа Колмогорова)
пределы функций (по Коши) - введены в 1960-х, убраны в 1970-х
производные - введены в 1960-х, с 1970-х даются на пальцах
приемы дифференцирования
анализ функций с помощью производных
интегралы - введены в 1970-х: неопределенные и определенные (нестрого)
Таким образом, американский школьный матан гораздо сложнее российского и по охвату тем больше похож на полтора-два семестра первого курса математических и математикоёмких специальностей в российских вузах. Однако он гораздо менее строг, чем последние, и задачи, которые там учат решать, проще Демидовича (вернее, в Демидовиче есть много задач такой сложности, какой в американских школах не дают).
Обеспечивается такой чудесный результат тем, что:
в США на матан идут только отборные школьники - опережающие среднюю программу и желающие совершенствоваться. Как правило они несколько старше российских 11-классников и стартуют с более высокого уровня релевантной математики (в алгебре они слабее, зато уже краешком изучали пределы)
в США матану уделяют раза в два больше времени, чем в России. Российский курс тянется немногим больше года по 3 45-минутных урока в неделю 8 месяцев в году, американский - 9 месяцев по пять 55-минутных уроков в неделю. Причем в российскую программу засовывают еще материал, с матаном не связанный.
Полагаю, иная ситуация в России на углублённом уровне математики: 8 часов математики в неделю (даже если "часы" 45-минутные, и половина из них идёт на геометрию и олимпиадную математику) при более высоком уровне предшествующей подготовки наверняка позволяют учить матан серьезнее, чем в США, если российская физмат-школа поставила это своей целью. Хотя обычно российские ФМШ предпочитают вместо сурового матана проходить теорию чисел, линейную алгебру и другие интересные ветви математики. (Этот абзац может быть интересен @LemurS в свете его комментария.)
Следующие статьи планирую посвятить: "продвинутому матану" (редкий в США курс), "линейке и дифурам" (почти недоступный курс, требующий опережения стандартной программы на три года), "основам статистики" и "преданализу".
Также, возможно, расскажу про "алгебру-2". Этот курс проходит большинство американцев, он не относится к "опережающей" математике, он еще слабый на фоне российской школы, но уже галопом по европам обгоняет её по охвату. Типичный ученик, изучавший "алгебру-2", ничего не научился решать, зато уже слышал про тригонометрию (напомню, вопреки массовым ложным воспоминаниям, что в России тригонометрию изучают только в 10 классе), логарифмы, комплексные числа, основную теорему алгебры.