Дата-сайнс, Машинное обучение
Ищу людей, кто работает по профессии дата-сайентист и инженер по машинному обучению.
Хочу взять у вас небольшое письменное интервью про карьеру 🌚
Маякните в комментариях со своим тг.
Выбор оптимального метода решения СЛАУ на основе анализа датасета
Полное руководство по выбору алгоритма для систем линейных уравнений
Меня зовут Руслан Сенаторов, я занимаюсь математическим обоснованием машинного обучения.
В этой статье, я расскажу как выбрать метод для определённого типа датасета, чтобы ваш код работал быстро, точно и без ошибок? И вы получили премию от руководства!
Введение
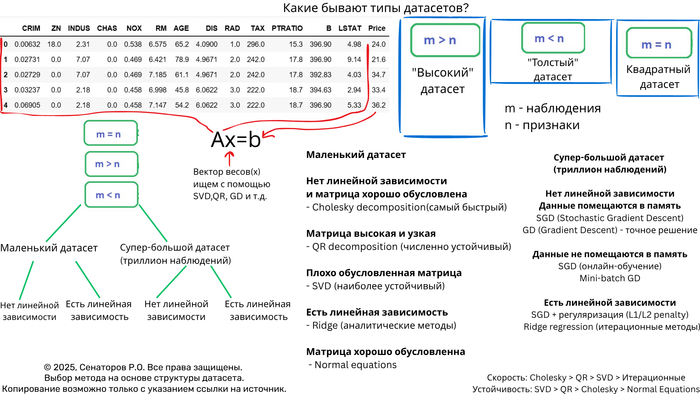
Решение систем линейных уравнений (СЛАУ) вида Ax = b — фундаментальная задача вычислительной математики и машинного обучения. Однако универсального метода не существует — выбор алгоритма критически зависит от характеристик датасета. Неправильный выбор может привести к катастрофическому замедлению вычислений или полной потере точности.
Ключевые характеристики датасета
1. Размер и структура матрицы
n_samples × n_features — соотношение наблюдений и признаков
Плотность/разреженность — процент ненулевых элементов
Обусловленность — число обусловленности матрицы
2. Вычислительные ограничения
Объем оперативной памяти
Требования к точности
Время вычислений
Дерево решений для выбора метода
Маленькие датасеты (n < 1000)
Плотные хорошо обусловленные матрицы
# Холецкий — самый быстрый для POSDEF матриц
if np.all(np.linalg.eigvals(A) > 0):
L = np.linalg.cholesky(A)
x = solve_triangular(L.T, solve_triangular(L, b, lower=True))
Матрицы общего вида
# QR-разложение — золотой стандарт
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
Плохо обусловленные системы
# SVD — максимальная устойчивость
U, s, Vt = np.linalg.svd(A, full_matrices=False)
x = Vt.T @ np.diag(1/s) @ U.T @ b
***
Средние датасеты (1000 < n < 10,000)
"Высокие" матрицы (n_samples >> n_features)
# QR остается оптимальным
# Сложность O(mn²) эффективна при m >> n
Q, R = np.linalg.qr(A)
x = solve_triangular(R, Q.T @ b)
"Широкие" матрицы (n_samples << n_features)
# Итерационные методы или регуляризация
from sklearn.linear_model import Ridge
model = Ridge(alpha=1e-6, solver='lsqr')
model.fit(A, b)
x = model.coef_
***
Большие датасеты (n > 10,000)
Разреженные матрицы
# Итерационные методы
from scipy.sparse.linalg import lsqr
x = lsqr(A, b, iter_lim=1000)[0]
***
Огромные датасеты (n > 1,000,000)
Стохастические методы
from sklearn.linear_model import SGDRegressor
model = SGDRegressor(max_iter=1000, tol=1e-3)
model.fit(A_batches, b_batches) # Мини-батчи
Когда использовать нормальные уравнения?
"Высокие" матрицы (m >> n)
# Решение через нормальные уравнения
x = np.linalg.inv(A.T @ A) @ A.T @ b
# Или более устойчивый вариант
x = np.linalg.solve(A.T @ A, A.T @ b)
10000 наблюдений и 50 фитч - Идеально для нормальных уравнений
cond_number = np.linalg.cond(A.T @ A) # < 10^8 Хорошо обусловленная
Детальный анализ методов
Точные методы (прямые)
Итерационные методы
SGD | Подходит для огромных данных | Медленная сходимость
Заключение
Выбор оптимального метода решения СЛАУ — это искусство баланса между точностью, скоростью и требованиями к памяти. Ключевые рекомендации:
Маленькие матрицы → Прямые методы (QR/SVD)
Большие разреженные → Специализированные разреженные решатели
Огромные плотные → Итерационные методы с предобуславливанием
Экстремальные размеры → Стохастическая оптимизация
Главное правило: Всегда начинайте с анализа структуры и свойств вашей матрицы — это сэкономит часы вычислений и предотвратит численные катастрофы.
Используйте это руководство как отправную точку для выбора оптимального стратегии решения ваших задач линейной алгебры.
История нейросетей
История нейросетей началась с идеи--попытки описать работу человеческого мозга языком математики. Это было в середине 20-го века, когда нейрофизиологи, математики и кибернетики начали работать вместе. Главными героями того времени стали Уоррен Мак-Каллок и Уолтер Питтс. В 1943 году они опубликовали статью, в которой предложили первую математическую модель искусственного нейрона. Эта модель, известная как нейрон Мак-Каллока-Питтса, была очень простой. Она работала по принципу "всё или ничего": принимала на вход сигналы в виде нулей и единиц, и если их сумма превышала определённый порог, нейрон "срабатывал" и выдавал единицу. Если нет--оставался пассивным и выдавал ноль. Но самое гениальное было в том, что они доказали: из таких простых "переключателей", соединённых в сеть, можно собрать машину, способную выполнить любую логическую операцию. По сути, они показали, что нейронная сеть теоретически не уступает по возможностям машине Тьюринга, дав биологическое обоснование самой идее вычислений. Они создали целую концепцию, где интеллект--это результат работы сложной сети взаимосвязанных вычислительных элементов.
Если Мак-Каллок и Питтс создали "скелет", то Дональд Хебб вдохнул в него жизнь, предложив концепцию обучения. В своей книге 1949 года он сформулировал знаменитый принцип, который часто описывают фразой "нейроны, которые активируются вместе, связываются вместе". Идея была в том, что связь между двумя нейронами усиливается, если они срабатывают одновременно. Это было первое научное объяснение того, как мозг может учиться и запоминать что-то, просто адаптируясь к поступающей информации. Этот принцип стал основой для многих будущих алгоритмов обучения, где веса соединений между нейронами--это не что-то застывшее, а переменные, которые меняются с опытом.
В 50-е годы эти идеи начали потихоньку воплощаться в железе. В 1951 году Марвин Минский и Дин Эдмондс построили SNARC--первую физическую нейросетевую машину. Этот "шкаф" из 3000 вакуумных ламп мог научиться находить выход из лабиринта. Но настоящую шумиху поднял Фрэнк Розенблатт, который в 1957 году представил "Перцептрон". Это была однослойная нейросеть для классификации, которая, в отличие от предыдущих моделей, могла по-настоящему учиться на данных, подстраивая свои веса. Розенблатт даже создал физическую версию, Mark I Perceptron, и делал громкие заявления, что его машина однажды сможет обрести сознание. Это вызвало огромный интерес и волну оптимизма. Примерно в то же время Бернард Уидроу и Тед Хофф разработали системы ADALINE и MADALINE. Они были более приземлёнными и решали конкретные задачи--например, успешно использовались для подавления эха на телефонных линиях. Это стало одним из первых коммерческих применений нейросетей и показало их реальный потенциал. К концу 50-х нейросети прошли путь от абстрактной теории до работающих устройств, заложив основу как для будущих прорывов, так и для грядущего разочарования.
Этот первоначальный оптимизм был заразителен, но, как оказалось, построен на довольно хрупком фундаменте. Период с конца 50-х до 80-х годов стал для нейросетей американскими горками: от эйфории до глубокого кризиса, известного как первая "зима искусственного интеллекта". Общественность и правительства, вдохновлённые Перцептроном Розенблатта, ждали появления разумных машин чуть ли не завтра. Финансирование лилось рекой, исследователи были полны энтузиазма.
А потом, в 1969 году, Марвин Минский и Сеймур Паперт опубликовали книгу "Перцептроны", которая стала для этой области холодным душем. Они математически доказали, что однослойный перцептрон, на который все возлагали такие надежды, имеет фундаментальные ограничения. Он просто не мог решить задачи, которые не являются "линейно разделимыми". Самый известный пример--логическая операция XOR ("исключающее ИЛИ"). Представьте, что вам нужно провести одну прямую линию на листе бумаги, чтобы отделить точки одного класса от другого. Для XOR это невозможно. Минский и Паперт убедительно показали, что для таких задач нужны многослойные сети, но как их эффективно обучать, тогда никто не знал. Их критика, исходящая от авторитетных учёных из MIT, оказалась убийственной. У фондов и исследователей пропал энтузиазм, и финансирование начало иссякать.
Причины "зимы ИИ" были не только в одной книге. В 1973 году в Великобритании вышел отчёт Лайтхилла, который раскритиковал всю область ИИ за невыполненные обещания. В США приняли поправку Мэнсфилда, которая требовала от военных агентств, вроде DARPA, финансировать только прикладные, а не фундаментальные исследования. К тому же, компьютеры того времени были слишком слабыми для обучения сложных моделей, а данных было мало. В это же время набирал популярность символьный подход к ИИ--системы, основанные на строгих правилах и логике. Они казались более понятными и надёжными, чем нейросети, которые работали как "чёрные ящики". В итоге исследования нейросетей на целое десятилетие ушли в тень.
Но даже в самые тёмные времена работа не останавливалась полностью. Некоторые учёные продолжали разрабатывать идеи, которые позже стали ключевыми. Например, Джон Хопфилд в 1982 году представил сети Хопфилда--рекуррентную сеть, которая работала как ассоциативная память. Она могла восстановить полный образ по его зашумлённому или неполному фрагменту. А Кунихико Фукусима в 1980 году разработал "Неокогнитрон"--многослойную иерархическую сеть, вдохновлённую строением зрительной коры мозга. В ней уже были заложены ключевые идеи современных свёрточных сетей: слои для извлечения локальных признаков и слои для их обобщения. Хотя эффективного алгоритма для обучения Неокогнитрона ещё не было, его архитектура стала прямым предком тех сетей, которые сегодня распознают лица на фотографиях.
Возрождение началось во второй половине 80-х, и его главной движущей силой стал один алгоритм--метод обратного распространения ошибки (backpropagation). Сама идея была известна и раньше, но именно статья Дэвида Румельхарта, Джеффри Хинтона и Рональда Уильямса 1986 года сделала её по-настояшему популярной и понятной. Этот алгоритм наконец-то дал эффективный способ обучать многослойные сети. Если говорить просто, он позволяет ошибке на выходе сети "путешествовать" в обратном направлении, от последнего слоя к первому, и на каждом шаге подсказывать нейронам, как именно им нужно изменить свои веса, чтобы в следующий раз результат был точнее. Это решило главную проблему, на которую указали Минский и Паперт, и открыло дорогу к созданию глубоких, сложных систем.
В это же время развивались и новые архитектуры. Появились рекуррентные нейронные сети (RNN), созданные для работы с последовательностями--например, с текстом или временными рядами. Однако у них была своя проблема: они плохо запоминали информацию на длинных дистанциях из-за так называемой проблемы исчезающих градиентов. Революционное решение в 1997 году предложили Зепп Хохрайтер и Юрген Шмидхубер, создав сети долгой краткосрочной памяти (LSTM). В них были специальные "вентили", которые позволяли сети самой решать, какую информацию из прошлого стоит запомнить, какую--забыть, а какую--использовать прямо сейчас. Это сделало их невероятно эффективными для задач вроде машинного перевода и распознавания речи.
Эти прорывы подкреплялись и практическими успехами. В 1985 году проект NetTalk показал, как нейросеть, обученная на словах, может научиться произносить их вслух. В лабораториях Bell Labs активно работали над распознаванием рукописного текста, что позже легло в основу систем автоматического чтения чеков. Даже появились первые специализированные "нейрочипы", которые пытались реализовать вычисления для нейросетей на аппаратном уровне. Хотя они не стали массовыми, это показало, что исследователи уже понимали: для серьёзных задач понадобится специальное железо.
В 90-е годы нейросети начали выходить из лабораторий и находить применение в реальном мире. Самым ярким примером стала работа Яна ЛеКуна и его команды в Bell Labs. В 1989 году они применили метод обратного распространения ошибки для обучения свёрточной нейронной сети, которую назвали LeNet. Её задачей было распознавание рукописных почтовых индексов. Успех был ошеломительным. К концу 90-х система на основе LeNet обрабатывала до 20% всех чеков в США. Это было первое крупное коммерческое применение глубокого обучения, которое доказало, что нейросети--это не просто академическая игрушка, а надёжная и прибыльная технология.
Тем временем LSTM-сети продолжали доказывать свою мощь в обработке речи. К 2007 году они начали превосходить традиционные подходы, а к 2015 году Google сообщила, что использование LSTM в системе распознавания речи на Android улучшило точность на 49%. Теория тоже не стояла на месте: в 1989 году была доказана теорема об универсальной аппроксимации. Она гласит, что нейросеть с одним скрытым слоем может аппроксимировать любую непрерывную функцию с любой желаемой точностью. Это дало прочное математическое основание для использования нейросетей в качестве универсальных "решателей" задач.
Параллельно шла подготовка к следующему рывку. Исследователи понимали, что для прогресса нужны две вещи: много данных и стандартные тесты для сравнения моделей. Примерно в 2007 году команда под руководством Фэй-Фэй Ли начала работу над проектом ImageNet--огромной базой данных из миллионов размеченных изображений. Позже на её основе был запущен ежегодный конкурс ILSVRC, который стал главным "олимпийским стадионом" для моделей компьютерного зрения. И, наконец, в 2009 году исследователи из Стэнфорда показали, что использование графических процессоров (GPU) может ускорить обучение нейросетей в 70 раз по сравнению с обычными процессорами. Все три компонента будущего взрыва--алгоритмы, данные и вычислительная мощность--были готовы.
Настоящая революция случилась в 2012 году. На том самом конкурсе ILSVRC команда Алекса Крижевского, Ильи Суцкевера и Джеффри Хинтона представила свёрточную нейросеть AlexNet. Она победила с таким ошеломительным отрывом, что это навсегда изменило мир ИИ. Её ошибка распознавания была на 10% ниже, чем у ближайшего конкурента. Секрет успеха был в комбинации нескольких факторов: очень глубокая архитектура, использование новой функции активации ReLU, которая ускоряла обучение, метод регуляризации Dropout для борьбы с переобучением и, самое главное,--обучение на двух мощных GPU. Эта победа стала сигналом для всех: глубокое обучение--это будущее. Крупные технологические компании вроде Google, Facebook и Microsoft начали массово инвестировать в эту область.
Успех AlexNet был бы невозможен без двух других "китов": больших данных, как ImageNet, и мощных вычислений на GPU. Графические процессоры, изначально созданные для игр, оказались идеально подходящими для параллельных вычислений, необходимых нейросетям. Это позволило обучать модели с миллионами и миллиардами параметров, что раньше было просто немыслимо.
После 2012 года начался взрывной рост. Исследователи стали создавать всё более глубокие и сложные архитектуры. VGGNet в 2014 году показала, что глубина решает. А в 2015 году появилась ResNet, которая решила проблему обучения сверхглубоких сетей с помощью "остаточных связей"--специальных "мостиков", которые позволяли градиенту беспрепятственно проходить через сотни слоёв. Благодаря ResNet в том же году компьютерное зрение впервые превзошло человеческие способности в задаче классификации на ImageNet. Появились и специализированные архитектуры вроде U-Net для сегментации изображений. Параллельно развивались фреймворки вроде TensorFlow и PyTorch, которые сделали разработку нейросетей доступной для тысяч инженеров и исследователей по всему миру.
С 2017 года начался новый этап, который можно назвать эрой универсальных моделей. Ключевым событием стала публикация статьи "Attention Is All You Need", в которой представили архитектуру "Трансформер". Она полностью отказалась от рекуррентных и свёрточных слоёв в пользу механизма "внимания". Этот механизм позволяет модели при обработке, скажем, слова в предложении, взвешивать важность всех остальных слов в этом же предложении одновременно, а не последовательно. Это не только ускорило обучение, но и позволило гораздо лучше улавливать длинные зависимости в данных. Трансформеры стали основой для гигантских языковых моделей, таких как BERT и GPT, которые демонстрируют поразительные способности в понимании и генерации текста. Позже эту архитектуру успешно адаптировали и для компьютерного зрения.
Одновременно произошёл бум в генеративном ИИ. Ещё в 2014 году Иэн Гудфеллоу представил генеративно-состязательные сети (GAN). В них две сети--генератор и дискриминатор--соревнуются друг с другом. Генератор пытается создать реалистичные данные (например, фото человека), а дискриминатор--отличить подделку от оригинала. В процессе этой "игры" генератор учится создавать настолько качественные подделки, что их не отличить от настоящих. Это привело к появлению таких систем, как DALL-E, которые могут генерировать сложные изображения по текстовому описанию. ИИ из инструмента анализа превратился в инструмент для творчества.
Несмотря на все успехи, сегодня перед нейросетями стоит несколько серьёзных вызовов. Во-первых, проблема "чёрного ящика": часто мы не можем точно объяснить, почему модель приняла то или иное решение. Это критично для медицины или беспилотных автомобилей. Для решения этой проблемы развивается нейро-символический ИИ, который пытается объединить обучаемость нейросетей с логикой и интерпретируемостью символьных систем. Во-вторых, огромная вычислительная стоимость. Обучение моделей вроде GPT-4 стоит сотни миллионов долларов и требует колоссального количества энергии, что поднимает экологические вопросы. В-третьих, этические проблемы: дипфейки, дезинформация, предвзятость в данных и влияние на рынок труда. Будущее нейросетей, вероятно, будет связано с поиском баланса между мощностью, эффективностью, безопасностью и прозрачностью.
Почему российские компании пока не могут создать такие же мощные нейросети как на Западе?
Вы замечали, что наши нейросети вроде неплохие, но всё же не дотягивают до западных моделей? Давайте разберёмся спокойно и по-честному.
💡 Главная причина - железо.
Современные нейросети обучаются на тысячах мощных видеокарт NVIDIA. Эти чипы производят в Тайване, и России они почти недоступны из-за санкций. Без них невозможно «прокачать» модель до уровня ChatGPT.
💰 Вторая - деньги и масштаб.
OpenAI, Google и Anthropic тратят миллиарды долларов на обучение. У нас таких инвестиций нет: даже Сбер и Яндекс работают в десятки раз меньших масштабах.
🧩 Ещё один барьер - данные.
Русскоязычных текстов в интернете меньше, чем англоязычных, и качество их ниже. Поэтому модели хуже чувствуют язык и контекст.
Но всё не так мрачно. Наши команды развиваются, появляются сильные локальные решения, и через несколько лет Россия вполне может догнать лидеров - если появятся ресурсы и свобода для настоящих прорывов.
Мой телеграм канал👉 Нейропоток
Бусификация по мнению AI модели Gemma3
Модель Gemma3:27b: https://ollama.com/library/gemma3
Запускаю Gemma3 для инференса через Ollama с веб-мордой openwebui локально на компе. Gemma — это семейство лёгких моделей от Google, созданных на основе технологии Gemini. Модели Gemma 3 являются многомодальными (обрабатывают текст и изображения) и имеют контекстное окно размером 128 КБ с поддержкой более 140 языков.
Roadmap linear regression (Структура методов линейной регрессии)1
Линейная регрессия — один из базовых методов статистического анализа и машинного обучения, предназначенный для моделирования зависимости отклика (зависимой переменной) от одной или нескольких независимых переменных.
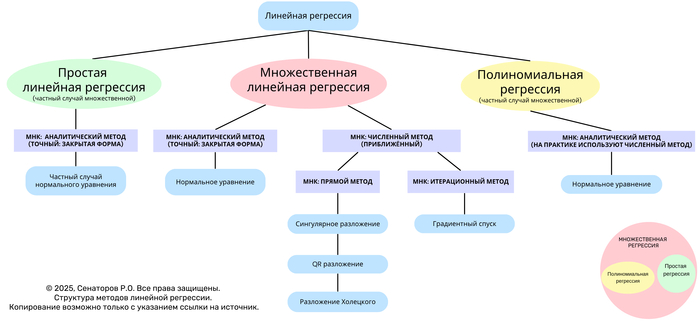
Данное дерево отражает иерархическую структуру основных видов линейной регрессии и методов решения задачи наименьших квадратов (МНК) — от аналитических к численным и итерационным.
Общая структура
На верхнем уровне различают три формы линейной регрессии:
Простая линейная регрессия — частный случай множественной, когда используется одна независимая переменная.
Множественная линейная регрессия — базовая форма, включающая несколько независимых переменных.
Полиномиальная регрессия — частный случай множественной, в которой вектор признаков дополнен степенными преобразованиями исходных переменных.
Методы наименьших квадратов (МНК)
Решение задачи линейной регрессии сводится к минимизации функции ошибок (суммы квадратов отклонений между наблюдаемыми и предсказанными значениями).
В зависимости от подхода различают аналитические, численные и итерационные методы.
1. Аналитический метод (закрытая форма)
Применяется, когда матрица признаков имеет полную ранговую структуру и система допускает точное решение.
Решение выражается формулой:
normal equation
Используется в простой и множественной линейной регрессии.
Базируется на нормальном уравнении.
2. Численные методы (приближённые)
Используются при больших объёмах данных или плохо обусловленных матрицах.
Основаны на разложениях матриц:
Сингулярное разложение (SVD)
QR-разложение
Разложение Холецкого
Обеспечивают численную устойчивость и более эффективные вычисления.
3. Итерационные методы
Применяются при очень больших данных, когда аналитическое решение невозможно вычислить напрямую.
Основной подход — градиентный спуск, при котором веса обновляются пошагово:
Особенности полиномиальной регрессии
Полиномиальная регрессия представляет собой множительную регрессию, где вектор признаков дополнен степенными функциями исходных переменных.
Хотя аналитическая форма возможна, на практике применяются численные методы, обеспечивающие стабильность и точность вычислений при высоких степенях полинома.
Взаимосвязь моделей
На схеме представлена визуальная взаимосвязь:
Простая регрессия — частный случай множественной.
Полиномиальная — частный случай множественной с расширенным базисом признаков.
Все три формы объединяются через метод наименьших квадратов.
Значимость статьи и вклад в Data Science
Представленный древовидный роадмап методов линейной регрессии является первой в истории попыткой системно и визуально объединить все формы линейной регрессии — простую, множественную и полиномиальную — через призму методов наименьших квадратов (МНК), включая аналитические, численные и итерационные подходы.
Традиционно в учебной и академической литературе методы линейной регрессии рассматриваются фрагментарно:
отдельно описываются простая и множественная регрессии,
разрозненно излагаются методы решения (нормальное уравнение, QR, SVD, градиентный спуск),
редко подчеркивается иерархическая связь между ними.
Разработанная структура впервые:
Объединяет все виды линейной регрессии в едином древовидном представлении, где показаны отношения "частный случай – обобщение".
Классифицирует методы МНК по принципу:
аналитические (точные, закрытая форма)
численные (разложения матриц)
итерационные (оптимизационные процедуры)
Визуализирует связь между теориями линейной алгебры и машинного обучения, показывая, как фундаментальные методы (SVD, QR, Холецкий, градиентный спуск) вписываются в единую систему.
Формирует когнитивную карту обучения — от интуитивных понятий к вычислительным и теоретическим аспектам, что делает её удобной как для студентов, так и для исследователей.
Научная и практическая новизна
Впервые создана иерархическая модель линейной регрессии, отражающая связи между всеми основными вариантами и методами решения.
Предложен универсальный визуальный формат (древовидный роадмап), который объединяет как статистическую, так и вычислительную перспективы анализа.
Показано, что полиномиальная и простая регрессии являются не отдельными методами, а вложенными случаями множественной регрессии.
Дана структурная типология МНК, которая ранее отсутствовала в учебных материалах и научных публикациях в таком виде.
Работа имеет прикладную значимость для Data Science, так как облегчает построение ментальной модели всех алгоритмов регрессии и их реализации в библиотечных инструментах (NumPy, SciPy, scikit-learn).
Вклад в Data Science
Для практиков Data Science роадмап служит навигационной схемой:
он показывает, какой метод выбрать в зависимости от типа задачи, объёма данных и требований к точности.Для преподавателей и студентов он обеспечивает структурную основу обучения, позволяя переходить от интуитивного понимания к строгим математическим методам.
Для исследователей — даёт целостное представление об эволюции МНК и связи между аналитическими и численными методами, что важно при разработке новых алгоритмов оптимизации и регуляризации.
До момента публикации не существовало единой визуальной структуры, описывающей всю иерархию методов линейной регрессии в рамках одной системы координат