Туманность Ориона
Икона в Храме глубокого космоса — Туманность Ориона — прекрасно видна невооруженным глазом на темном небе. Но попалась на глаза астрономам она только лишь в эпоху первых телескопов, и открыта эта грандиозная туманность была с помощью телескопа, причем, далеко не сразу.
Галилео Галилей неоднократно наблюдал центральную часть астеризма “Меч Ориона”, и даже открыл тройственность центральной звезды в нем — Теты Ориона. Но туманность, опутывающую звезду в Мече, Галилей не заметил. Может дело было в особенностях оптики первых телескопов Галилея — она была довольно темной, не светосильной. Однако, его современники — Никола-Клод Фабри де Пейреск, Иоганн Баптист Цизат, Джованни Баттиста Годиерна — тогда уже вооруженные оптикой, независимо друг от друга наблюдали “яркое, мерцающее облако” вокруг центральной звезды Меча Ориона. Но в те годы сами телескопы распространялись по Миру гораздо быстрее, чем результаты проведенных с их помощью наблюдений. Уже в 1610 году — буквально в год сенсационной премьеры Галилея — телескопами обзавелись десятки астрономов и даже европейских университетов (это никем не запрещалось). Но отчеты о наблюдениях оставались приватными. К тому же, тогда не существовало ни электронной почты, ни социальных сетей. До сих пор историки находят в архивах тех или иных заведений неопубликованные результаты наблюдений и меняют имя первооткрывателя той или иной туманности. Не так давно стало известно, что первым европейским наблюдателем, обнаружившим Туманность Ориона в телескоп, был Никола-Клод Фабри де Пейреск.
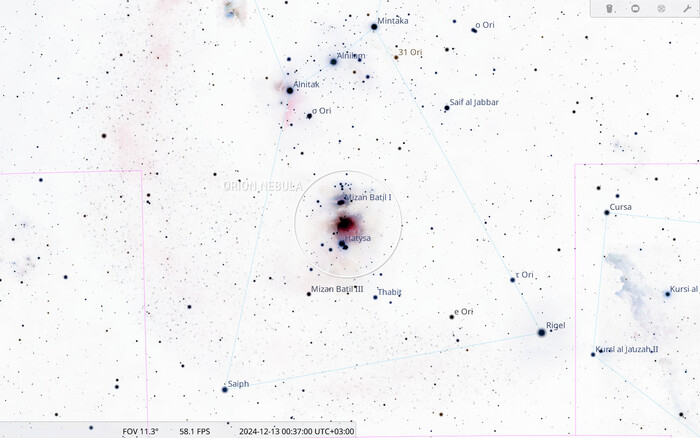
Расположение Туманности Ориона на звёздной карте в южной части одноименного созвездия — под трехзвёздным Поясом Ориона, вокруг центральной звезды астеризма «Меч Ориона»
Вместе с этим существуют интерпретации мифологических преданий индейцев Майя, что те видели Туманность среди звезд созвездия Ориона (разумеется, у индейцев в этой части неба было совсем другое созвездие). Но всерьез относиться к этим интерпретациям вряд ли стоит. Скорее всего они проистекают из современного тренда на преувеличение значения и развитие культа тайных знаний в наследиях неевропейских культур.
Стоит вспомнить, что, например, индейцы центральной Америки в упор не видели подплывающие к берегу корабли Колумба — просто потому, что не ожидали увидеть корабли, плывущие оттуда, где по представлению коренных народов Америки нет ничего.
По той же причине астрономы античности и средних веков не видели Туманность Ориона невооруженным глазом. В те эпохи состояние атмосферы и отсутствие светового загрязнения всячески способствовали тому, чтобы туманность была обнаружена. Но этого не случилось — вплоть до первых телескопических наблюдений.
Автор этого рассказа видел Туманность Ориона глазом неоднократно. Всякий раз, когда оказывался в Крымской Астрофизической Обсерватории Зимой, я любовался её сиянием на зимнем небе Крымских гор, которые совсем не высоки, но уже попадали в неуклонно расширяющуюся зону светового загрязнения. Однако, я знал, что центральная звезда в Мече Ориона окутана Туманностью, и потому светится так необычно — она словно пушистая и слегка размытая — не такая точечная, как прочие звёзды в её окружении.
Можно предположить, что довольно яркая для абсолютно черного неба Балкан Тета Ориона и не позволила отчетливо увидеть туманность астрономам античной Греции — увидели звезду, и успокоились. А то, что она странная — ну, мало ли странного на небе…
Астеризм «Меч Ориона» на звёздной карте — крупным планом. В центре Большая и Малая Туманности Ориона — практически слившиеся. Над ними еще одна туманность — «Running Man Nebula» (Туманность Бегущий Человек)
Однако, с того времени, как знание об этой туманности стало достоянием научной общественности, она стягивала на себя значительную долю внимания наблюдателей. Туманность стали называть Great Orion Nebula — Большая (или даже — Великая) Туманность Ориона. Этому же способствовало обнаружение поблизости от неё еще одной туманности, которую какое-то время называли Малой Туманностью Ориона, пока не пришли к выводу, что это всё одно и то же туманное образование. Теперь этот небольшой фрагмент называется Туманность де Мерана (по имени её открывателя — Жана Жака де Мерана). Шарль Мессье внес в свой каталог Большую и Малую Туманности Ориона под разными номерами — M42 и M43 соответственно, да и в Новом Общем Каталоге они фигурируют как разные объекты — NGC 1976 и NGC 1982, хотя даже на любительских современных снимках (равно как и при наблюдении в совсем небольшие телескопы) обе эти туманности сливаются воедино.
К слову будет сказать, что Туманность Ориона столь велика в визуальном плане, что астрономам (но чаще — с подачи любителей) пришлось выдумать отдельные названия для описания тех или иных её фрагментов — “Темный залив”, “Большой залив”, “Рыбья пасть”, “Меч”, “Выпад”, “Парус” — все эти неофициальные “провинции” туманной “империи” нанесены на любительские и профессиональные карты Туманности Ориона. Иначе, в её сияющих волокнах, плазменных течениях и пылевых туннелях можно было заблудиться.
Каждый новый этап в изучении Туманности Ориона поражал воображение исследователей, и приносил с собой удивительные откровения об устройстве Вселенной.
Уильям Гершель впервые высказал предположение, что Туманность Ориона являет собой скопление материала для формирования звёзд, которые еще не родились. В его эпоху доказать или опровергнуть столь смелые высказывания не представлялось возможным. Но более поздние исследования подтвердили, что здесь действительно происходит рождение новых светил, а Туманность Ориона есть ни что иное, как один из крупнейших регионов звёздообразования Галактики.
Туманность Ориона удостоилась чести стать первой в истории Туманностью, которую удалось сфотографировать. На первом же снимке, сделанном в 1880 году Генри Дрейпером, проявилась сложнейшая детализация этой космической субстанции, похожей на гигантский цветок, которая надолго озадачила ученых — все эти волокна, темные и светлые прожилки — свидетельствовали о бурных процессах, происходящих на наших глазах. И действительно — сравнение фотографий, сделанных в разные годы, обнаруживало неожиданную динамику туманности — туманность живет и видоизменяется буквально на глазах ученых. Конечно, для этого требовалось время, но чем зорче становились телескопы, тем явнее становились изменения в облике Туманности Ориона, особенно её центральной части.
Сердцем Туманности Ориона является так называемая “Трапеция Ориона” — в прошлом кратная звезда, а теперь статус этой звездной системы поднялся до рассеянного звездного скопления.
Центральная звезда в “Мече Ориона” представляет собой так называемую “широкую пару” — легко разделяемую в самую лёгкую оптику (наиболее зоркие люди могут разделить Тету 1 и Тету 2 и без оптики — между ними что-то около 3 минут дуги, как у компонентов Эпсилон Лиры).
Более северная и западная из Тет — Тета 1 — как раз и выглядит как “Трапеция” — 4-звёздная система отчетливо голубых (если не сказать — синих) звезд. Три из них обнаружил Галилей, а четвертую — чуть более поздние наблюдатели его же эпохи. Само название “Трапеция Ориона” ввел Роберт Джулиус Трюмплер (американский астроном) в 1931 году, хотя к тому времени в системе было уже надежно подтверждено 8 компонентов, и дальше их число только увеличивалось. Сейчас Тета 1 считается 16-кратной системой, некоторые компоненты которой обнаруживают себя лишь периодическим доплеровским смещением линий в спектре, или затменными эффектами. А кроме этого в скоплении “Трапеция Ориона” выявлено множество таких звезд, чья судьба до недавнего времени была не определена — их скорости казались чрезмерными для устойчивого длительного пребывания в составе скопления. Одна из современных гипотез, объясняющая столь высокие скорости некоторых звезд скопления, помещает в центр системы Теты 1 Ориона черную дыру массой около 100 масс Солнца — тогда всё сходится, и скопление “Трапеция Ориона” становится устойчивым. А если нет — оно бы давно распалось.
Трапеция Ориона крупным планом и центральная часть Туманности. Изображение полученно с помощью Космического Телескопа имени Джеймса Уэбба (JWST)
Хотя, временной параметр “давно” требует объяснений.
Все наблюдаемые в Туманности звезды (равно, как и сама Туманность Ориона в её современном виде) — очень молодые жители Вселенной. Например, возраст голубых и крайне горячих гигантов с Трапеции Ориона не превышает 3 млн.лет — они буквально ровесники всего Человечества. И именно благодаря излучению этих звезд мы можем наблюдать всю Туманность. Остальные её светила обеспечивают лишь 10-15% ионизации межзвездного газа. Без Трапеции здесь была бы так-себе туманность, быть может и массивная, с большим потенциалом, но совершенно незаметная на фоне прочих туманных образований, коими окутано все созвездие.
Звёзды Трапеции Ориона не только обеспечивают Туманности её заметность, они постепенно рассеивают материал туманности — их мощные звездные ветры разгоняют вещество, из которого относительно недавно они сами родились, на периферию туманности, где облака водорода уже не будут ничем столь же ярко подсвечиваться. Хотя, не исключено, что ударная волна, которую гонят звёздные ветры Трапеции, приведет к уплотнению материи и рождению новых звезд, которые окажутся не менее массивными, горячими и яркими.
Как конкретно будет развиваться судьба Туманности Ориона, это ученым еще предстоит выяснить. И во многом по этой причине к туманности Ориона в последние десятилетия приковано пристальное внимание крупнейших телескопов — земных и космических.
Протопланетный диск Proplyd 106-417 в Туманности Ориона. Изображение получено с помощь Космического Телескопа имени Эдвина Хаббла
Оказалось, большая часть жителей Туманности — коричневые карлики — объекты, занимающие промежуточное положение между звёздами и планетами. Их здесь тысячи, а может и десятки тысяч — посчитать их всех очень сложно, ведь они почти не светятся в видимом диапазоне спектра, и только недавно введенный в строй телескоп имени Джеймса Уэбба, изучающий Вселенную в инфракрасном свете, выявил в туманности Ориона множество коричневых карликов, и даже открыл первую двойную систему, где оба компонента — коричневые карликовые.
Здесь же — в туманности Ориона — были обнаружены первые планеты-изгои, существующие отдельно от каких-либо звёзд, гравитационно ни с чем не связанные, а просто дрейфующие по Туманности.
Большая часть голубых гигантов, из которых сложена фигура созвездия Ориона, рождены в Туманности Ориона, но покинули её в результате неустойчивых гравитационных взаимодействий. Туманность, словно праща, выбрасывает звезды прочь, чтобы не мешали своими звёздными ветрами процессу творения новых светил. Некоторые изгнанники Туманности успели добраться до соседних созвездий. Выявлено как минимум три заметных и быстрых звезды, покинувших Туманность Ориона в её обозримом прошлом. Это звёзды Mu Голубя, AE Возничего и 53 Овна. Исследование траекторий их движения привели ученых назад — к “Трапеции Ориона”, откуда перечисленные светила были выброшены несколько миллионов лет назад. Сейчас они удаляются от места своего рождения со скоростью превышающей 100 километров в секунду.
Около некоторых звезд, погруженных в Туманность Ориона методом прямого наблюдения выявлены протопланетные диски. Это опять заслуга телескопа Джеймса Уэбба и его инфракрасных коллег. У ученых нет уверенности в том, что любой протопланетный диск доэволюционирует до полноценной и устойчивой планетной системы, поскольку оценить разрушающее влияние звездных ветров от голубых гигантов Туманности во всей её протяженности сложно. Однако, открытия протопланетных дисков у звезд в Туманности Ориона свидетельствует о том, что формирование таких дисков является единым процессом вместе с формированием самой звезды.
Меч Ориона и Туманность Ориона в горизонтальной ориентации. Изображение полученно с помощью Обзорного Инфракрасного Телескопа VISTA
Туманность Ориона не кончается там, где на самых детальных астрофотографиях гаснет сияние её волокон — её материя простирается и дальше, заполняя собой все пространство в пределах созвездия Ориона (на некоторой дистанции от Солнечной системы). Это покажется странным, но астрономы — при всем их внимании к этой туманности — не могут назвать точного расстояния до неё. Опубликованная во многих источниках величина является скорее итогом некоторого соглашения — 1300 световых лет. Хотя некоторые исследования дают разброс значений от 1000 до 1600 световых лет. Истина, скорее всего, где-то посередине, но это уже не самое научное предположение.
Исходя из современных оценок расстояния до туманности, её линейные размеры составляют 25x35 световых лет (речь, конечно же, о видимой — проявленной — части туманности), а Масса составляет около 10 тысяч солнечных масс. При этом, звездное население пределов Туманности (за вычетом коричневых карликов) оценивается в несколько тысяч звёзд.
Созвездие Ориона и Молекулярный облачный комплекс Ориона. Туманность Ориона едва ли бросается в глаза на этом замечательном снимке, автора которого зовут Rogelio Bernal Andreo
На зимнем небосводе с Туманностью Ориона соседствуют множество других туманностей, иногда не менее впечатляющих. Большинство из них действительно связаны с Туманностью Ориона и вместе образуют так называемый “Молекулярный облачный комплекс Ориона”. Пару десятилетий назад мы лишь слышали о таком, но — не видели. Теперь же — с развитием технологий в области любительской астрофотографии — практически каждый начинающий астрофотограф способен запечатлеть всё газопылевое богатство спирального рукава Персея-Ориона, в котором, хоть и немного с краю, держит свой галактический путь Солнце со свитой планет. К счасть, путь пролегает вдали от столь впечатляющих туманных структур, и поэтому нам здесь хорошо и спокойно (правда, мы это не очень ценим). Но истоки нашего существования уходят в те галактические дали, полные туманных и пылевых завихрений, где около 5 миллиардов лет сформировалось Солнце и каким-то образом обзавелось планетами. И лучшего места для этого, чем грандиозная водородная туманность с извилистыми прожилками пылевых волокон, в Галактике не сыскать — в разреженной межзвёздной среде не родятся ни звёзды, ни планеты. Но когда уже все главное создано, жить лучше подальше от эпицентра звёздообразования. И как можно заметить, примерно так всё во Вселенной и происходит. Туманности рождают звёзды, а звёзды рассеивают туманности, и разбрасывают друг друга в разных направлениях, чтобы не создавать излишнюю суету в небольшом пространстве.
Когда Туманность Ориона окончательно рассеется, на её месте на какое-то время останется красивое и яркое скопление, напоминающее Плеяды, а потом распадется и оно. И только тогда на планетах вокруг тех звёзд, которые доживут до лучших времен, воцарятся наиболее благоприятные условия для столь хрупкого вселенского явления, которое мы ассоциируем со словом “жизнь”.
Подбирая главную иллюстрацию для этого рассказа я долго не мог остановиться в выборе. Не исключено, что Туманность ориона лидирует по количеству совершенно невероятных по зрелищности снимков, сделанных как профессионалами, так и любителями. В итоге, по необъяснимым причинам "победила" астрофотография от совершенно неизвестного астрофотографа Itto Ogami (мне не удалось отыскать его нигде, кроме как на сайте astrobin.com), и скорее всего здесь использован псевдоним. Тем не менее, изображение действительно превосходное. На нем, помимо Туманности Ориона, поместилась и туманность "Бегущий человек", напоминающая о том, что даже Великая Туманность Ориона является частью чего-то чего-то большего.
Туманность Ориона (справа) и туманность Бегущий Человек (в левой части кадра - в ней преобладают синие и голубые оттенки). Автор астрофото Itto Ogami
Ссылка на оригинальное изображение: https://www.astrobin.com/gsyei2/
В видеоролике (с него начинается рассказ) звучит музыка из студийной экспериментальной сессии











![15.04.1452 - День рождения Леонардо да Винчи [вехи_истории] Наука, Ученые, История (наука), Инженер, Технологии, История науки, Научпоп](https://cs17.pikabu.ru/s/2025/04/13/16/oml6zl2w.jpg)