Хуягэ, гондонягэ, выблядгэ – это самый обыкновенный школьный тест, такой же, как впр или какая-нибудь контрольная работа. Готовиться конечно надо – там почитать, порешать что-то и дальше продолжить веселиться, но мои родители так не думали. Они тратили туёву хучу денег на всяких репетиторов – хоть их не было так много в моей жизни – занятие один час в неделю, но тем не менее, можно было обойтись и без них и как я писал ранее – почитать, порешать что-то и не рвать жопу, как будто это конец света. Я искренне надеюсь на то, что это особо не повлияло на меня в дальнейшем, мой мозг стёр всё то, что мне там вдалбливали и я веду себя так, как будто к этим репетиторам никогда и не ходил. Так или иначе, я стараюсь воспринимать это просто как дополнительные занятия, чтобы лучше разбираться в той или иной сфере, как танцы или рисование, куда меня также отправляли

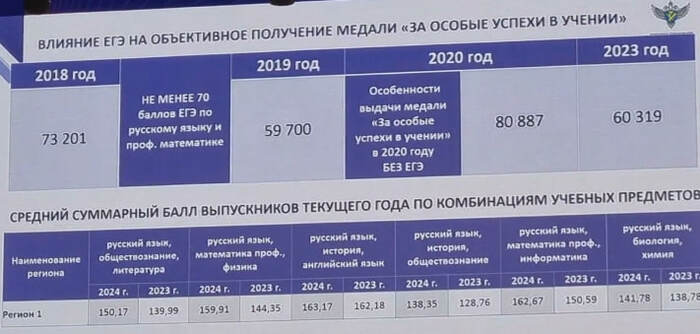
В своем выступлении Анзор Музаев напомнил о коррупции в школах до ЕГЭ. В качестве еще одного доказательства описал ситуацию с получением золотых медалей. Когда их количество менялось в зависимости от того, сравнивался ли аттестат медалистов с их результатом на ЕГЭ или нет.

Тут надо сказать, что коррупция размножается там, где у людей есть возможности для обогащения за счет других. На всех уровнях образования такие возможности есть, глупо с этим спорить. Их несоизмеримо меньше, чем, например, у чиновников. Но они есть и каждый педагог может вспомнить коллег или руководство, которые любят и даже выпрашивают дорогие подарки, давят на подчиненных, чтобы те поставили нужную отметку правильному ученику и т.д. Совсем недавно, например, был громкий скандал со студентами-медиками. Ну нельзя же этого просто не замечать!

Следующим важным тезисом стало заявление о работе по связи электронного портфолио ученика с внешними источниками. По замыслу, кроме баллов ГИА должно учитываться и это.

Замечу, что те же нормы ГТО повсеместно покупаются. Как это будет учитывать РОН и нужно ли оно вообще – огромный вопрос.

Дальше Музаев сказал, что ректор «Горного» уже начал учитывать балл аттестата в качестве интегральной оценки. И возможно, именно этот опыт надо будет расширять. Напомню, что сам ректор как раз об этом не сказал ни слова. За что, честно говоря, к нему так и хочется прицепить несколько нелицеприятных эпитетов.

Закончил руководитель Рособрнадзора тем, что никаких маркеров, которые бы указывали на объективность оценок аттестата нет. И если получится их создать, то идея интегральной оценки (очевидно, в варианте Литвиненко) получит право на жизнь.

Я сейчас не буду писать о том, как это можно и нужно делать – напишу в завершении цикла.

Подводя итог скажу, что Музаев, как и Литвиненко с Фадеевым, очень мало говорил по заявленной теме. Однако, фактически, он сделал две вещи:

1. Он легализовал подход Литвиненко, который своей волей довольно бестолково собирается учитывать при поступлении отметки аттестата в дополнение к ЕГЭ. Легализовал, хотя сам и указывал на вероятность нечестности при выставлении этих отметок.

2. Немного забегу вперед и скажу, что никто из присутствующих четко не обратил внимание на недопустимость внедрения переводных экзаменов без устранения принципиальных проблем. Этим и воспользовался Музаев, начав продвигать ВПР в качестве таких экзаменов. Ведь их на конференции прямо поддержали почти все «авторитетные директора и учителя».

В итоге мы вернулись назад, ведь «припоминать» близко по значению к глаголам «укорять» и «упрекать» — словам, с которых все началось. Мы словно вместе попали во временную петлю! 😄

За 20 минут учащиеся узнали более 10 слов! Так, обычный урок по видам односоставных предложений превратился в увлекательное путешествие по глаголам русского языка.

С одной стороны, меня очень удивило незнание столь многих слов довольно взрослыми учащимися — восьмиклассниками. С другой, подобное сейчас не редкость.

Практически каждый урок ученикам любого года обучения попадаются неизвестные слова. Безусловно, я каждое из них объясняю, обогащая лексический запас ребят.

Я задумалась, почему эта тенденция распространена и обнаружила несколько очевидных причин. Поговорим о них в следующем посте.

Но пока хочу спросить вас: какие причины незнания многих слов современными учащимися видите вы?

Приглашаю в свой ТГ-канал, ссылка в шапке профиля