Квантовые алгоритмы для восстановления траекторий частиц: новый подход
Автор: Денис Аветисян
Исследователи предлагают использовать методы Монте-Карло с поиском по дереву для автоматической разработки квантовых схем, применяемых к сложной задаче реконструкции траекторий частиц.
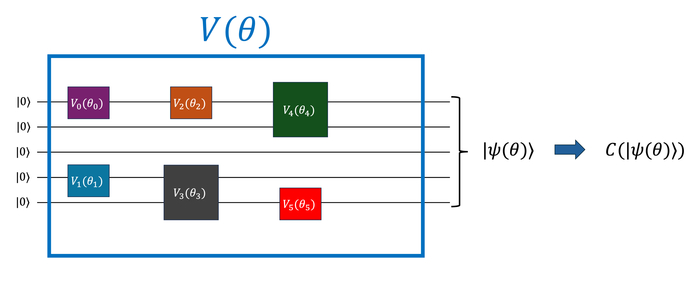
В задачах квантового вариационного решения, цель состоит в определении упорядоченной последовательности квантовых вентилей Vi(thetai), составляющих вариационное состояние V(θ)ket0, оптимизирующего заданную целевую функцию C.
В данной работе изучается применение вариационных квантовых алгоритмов и методов Монте-Карло с поиском по дереву для автоматического проектирования квантовых схем, предназначенных для восстановления траекторий частиц.
По мере роста объемов данных, получаемых в экспериментах по физике высоких энергий, традиционные методы реконструкции траекторий частиц сталкиваются со значительными вычислительными трудностями. В работе «Variational Quantum Algorithms for Particle Track Reconstruction» исследуется потенциал вариационных квантовых алгоритмов для решения этой задачи, в частности, посредством автоматизированного проектирования квантовых схем. Показано, что использование метода Монте-Карло поиска по дереву (MCTS) позволяет эффективно разрабатывать квантовые анзацы, приспособленные к геометрии конкретного детектора, и находить решения для различных масштабов задачи. Возможно ли дальнейшее совершенствование алгоритмов квантового проектирования для преодоления текущих ограничений и реализации квантового преимущества в обработке данных физики высоких энергий?
Восстановление Частиц на LHC: Преодоление Вычислительных Преград
Высокоэнергетические столкновения частиц на Большом адронном коллайдере (LHC) генерируют огромные объемы данных, регистрируемые детекторами, такими как VELO. Восстановление траекторий частиц из этих данных представляет собой серьезную вычислительную задачу, ограничивающую скорость анализа и, следовательно, возможности для новых физических открытий. Традиционные методы сталкиваются с трудностями, обусловленными комбинаторной сложностью реконструкции траекторий на фоне значительного уровня шума и случайных событий, что требует разработки инновационных алгоритмов и вычислительных стратегий для эффективной обработки и интерпретации данных, полученных на LHC.
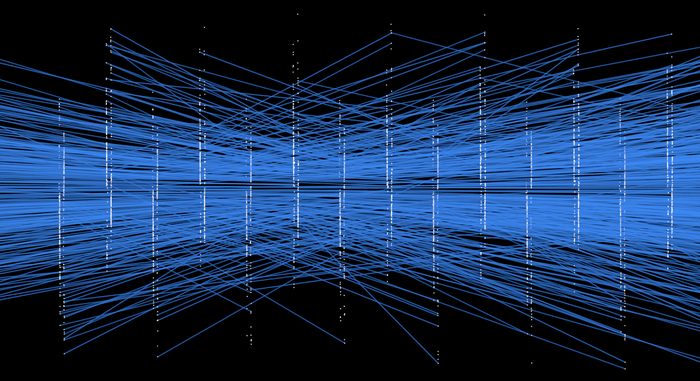
Данные, полученные с детектора VELO коллайдера LHCb, демонстрируют зарегистрированные частицы в виде отдельных треков (синие линии) и точек попадания (белые точки).
Превращение реконструкции траекторий частиц в квантовую задачу
Реконструкция траекторий частиц может быть эффективно представлена как задача оптимизации, в частности, как задача двоичной квадратичной оптимизации без ограничений (QUBO), что делает её подходящей для решения с использованием квантового отжига и вариационных квантовых алгоритмов. Для дальнейшей обработки задача моделируется с использованием гамильтонианов Изинга, обеспечивая стандартный формат для квантовой обработки. Такое преобразование позволяет использовать возможности квантовых алгоритмов для определения оптимальных конфигураций траекторий в условиях сложного потока данных, получаемых от детекторов, и значительно повысить точность и эффективность реконструкции.
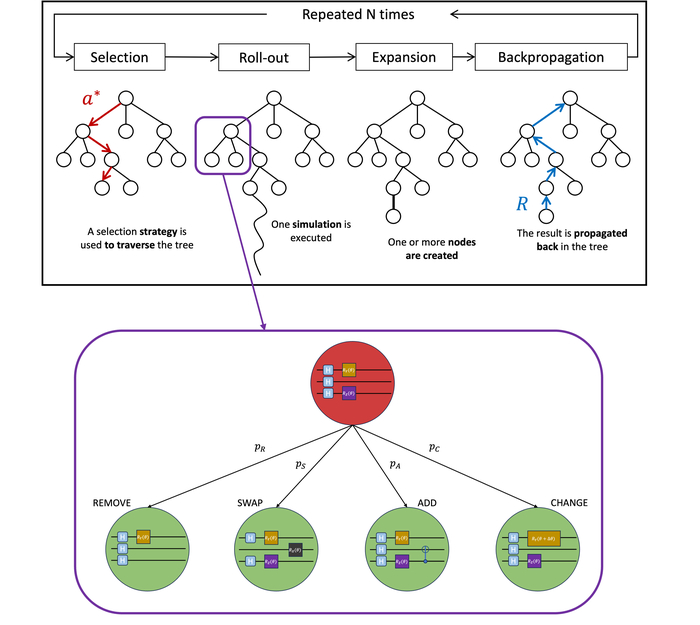
В нашей системе QAS для проектирования квантовых схем используется метод поиска по дереву Монте-Карло, в котором пространство действий определяется дискретизацией непрерывного множества возможных модификаций схемы.
Квантовые алгоритмы для точной реконструкции траекторий
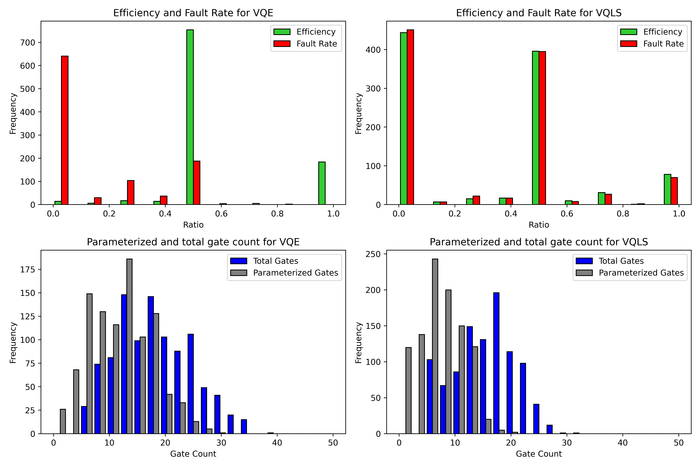
Исследования направлены на применение квантовых алгоритмов для повышения точности реконструкции траекторий элементарных частиц. В качестве перспективных подходов рассматриваются вариационный квантовый решатель собственных значений (VQE) и вариационный квантовый решатель линейных уравнений (VQLS), использующие параметризованные квантовые схемы, известные как квантовые анзацы. Для эффективной разработки и оптимизации этих анзацев для конкретной задачи реконструкции траекторий применяется метод Монте-Карло с деревом поиска. Полученные результаты демонстрируют, что VQE превосходит VQLS по эффективности в идентификации корректных траекторий, в то время как альтернативные алгоритмы, такие как квантовый отжиг и алгоритм Харроу-Хассидима-Ллойда (HHL), сталкиваются с практическими трудностями, связанными с глубиной схемы и когерентностью кубитов. Максимальная глубина, использованная в квантовых схемах в ходе данного исследования, составляла 50.
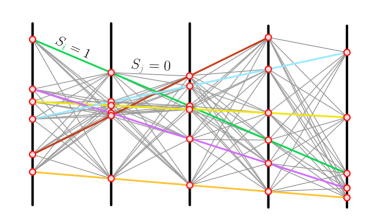
В представленной модели с пятью детекторами и шестью частицами, треки частиц выделяются из комбинаторного фона путём соединения сигналов (красные кружки) в слоях детектирования в сегменты, формирующие полные треки.
Оптимизация и Проверка: Путь к Практическому Квантовому Трекингу
Для эффективной тренировки вариационных квантовых схем применяется правило сдвига параметров, позволяющее вычислить необходимые градиенты. Ключевым аспектом реализации вариационных квантовых алгоритмов обучения на существующем квантовом оборудовании является разложение Паули. Первоначальное тестирование и валидация проводились на упрощенных моделях детектора VELO, с использованием вычислительных ресурсов в 10⁴ для задач с n le 5 кубитов и 10⁵ для больших значений n. Это позволило оценить эффективность предложенного подхода и выявить потенциальные области для дальнейшей оптимизации.
Квантовые Графовые Нейронные Сети: Взгляд в Будущее
Перспективным направлением исследований представляется применение квантовых графовых нейронных сетей (QGNNs) к задаче реконструкции траекторий частиц, поскольку их архитектура естественным образом соответствует графовой структуре данных, что потенциально способно повысить точность анализа. Объединение QGNNs с вариационными алгоритмами, описанными ранее, может привести к созданию мощного гибридного квантово-классического подхода к решению сложных задач в физике частиц. Дальнейшее развитие квантового оборудования и алгоритмических методов является ключевым условием для реализации полного потенциала квантовых вычислений и расширения их применения в экспериментальных и теоретических исследованиях, позволяя решать задачи, недоступные для классических вычислительных систем, и открывая новые горизонты в изучении фундаментальных законов природы.
Исследование автоматического проектирования квантовых схем посредством Monte Carlo Tree Search (MCTS) вызывает особенный интерес. В попытке обуздать хаос, порождаемый сложными задачами реконструкции траекторий частиц, авторы предлагают не просто алгоритм, но и своего рода ритуал, где каждая итерация MCTS – это попытка уговорить квантовую систему выдать желаемый результат. Как говорил Нильс Бор: «В физике нет ничего абсолютного, всё относительно». И в данном случае, относительность заключается в постоянном поиске оптимальной структуры квантовой схемы, ведь идеальное решение, вероятно, скрывается лишь за горизонтом текущих вычислений. Данная работа демонстрирует, что даже в мире квантовых вычислений, где надежды на абсолютную точность высоки, необходимо помнить о природе хаоса и относительности истины.
Куда же всё это ведёт?
Представленные изыскания, как и любое заклинание, лишь отсрочили неизбежное столкновение с хаосом. Автоматизированный поиск анзацев, безусловно, облегчает жизнь алхимику, но не избавляет от необходимости смириться с тем, что идеального решения не существует. Каждый найденный квантовый путь – это не триумф над шумом, а лишь временное умиротворение, призрачная надежда, что траектории частиц хоть ненадолго подчинятся воле алгоритма.
Очевидно, что дальнейший прогресс потребует не только совершенствования методов поиска анзацев, но и переосмысления самой постановки задачи. Искать точное восстановление траектории – утопия. Гораздо перспективнее научиться извлекать полезную информацию из неполных, зашумленных данных, украшать хаос, а не пытаться его победить. И, конечно, необходимо признать, что увеличение масштаба задачи неизбежно столкнёт с ограничениями текущего квантового железа – и тогда придётся искать новые способы обмана реальности.
В конечном счёте, задача восстановления траекторий частиц – это лишь повод для экспериментов. Истинный интерес заключается в поиске универсальных методов адаптации квантовых алгоритмов к различным типам шума и неточностям. Данные всегда правы – пока не попадут в прод. И тогда придётся изобретать новые заклинания.
Оригинал обзора с формулами: denisavetisyan.com/kvantovyj-poisk-traektorij-novyj-podhod-k-rekonstrukczii-chasticz
Оригинал статьи: https://arxiv.org/pdf/2511.11397.pdf
Связаться с автором: linkedin.com/in/avetisyan