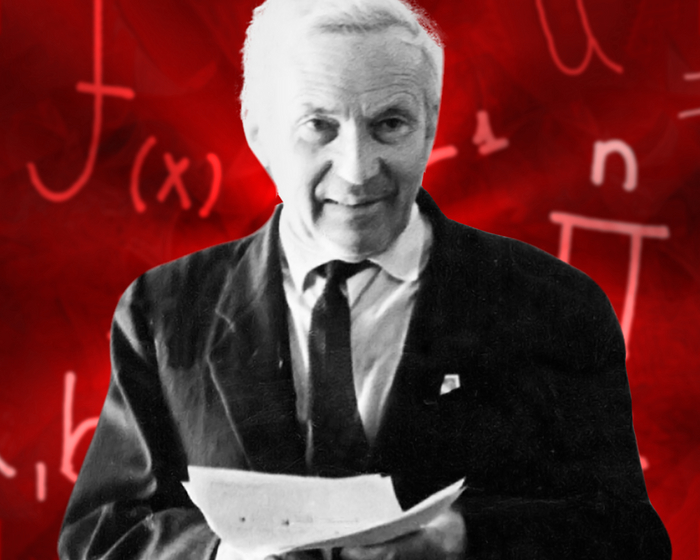Сложная задача
Приветствую, уважаемые математики. Может, кто-нибудь может решить задачу 3.34? Сколько ни пытался, не получалось, и в интернете ничего нет
Лига математиков
905 постов
•
2 484 подписчика
0 просмотренных постов скрыто
Срочно, кто может помочь с решением криволинейных интегралов?
Показать полностью
5
[Вопрос] Метод комплексных амплитуд
Приветствую. Помогите разобраться. В гугле в основном попадаются стати по применению метода, а вот выводов и обоснования я так прям просто не нашел. Вопрос, собственно, вот в чем - каково строгое математическое обоснование этого метода? Нельзя же просто так взять, и заменить действительную функцию комплексной. А потом, после решения в комплексных числах, комплексную - действительной. Нужно ведь доказать, почему после этих трансформаций мы получили решение исходной задачи а не хз чего. Я так предполагаю, что это обоснование делается при помощи выражения косинуса через полусумму комплексных экспонент, но не уверен...
P.S. Для любителей пошутить про ЕГЭ и домашку - я учебу закончил 10 лет назад.
Ищу респондентов для научного исследования
Добрый день!
Меня зовут Ковешникова Екатерина и я магистр социальной психологии. Мои аккаунты в соц. сетях: insta @psy_kovesh , telegram Katerina_oom .
Верю в теорию рукопожатий и силу Интернета! ))
Для написания ВКР ищу респондентов!
Честно, исследование долгое, ведь Наука- дело небыстрое!) Исследование рассматривает предпочтение к виртуальному/ реальному общению, самооценку, субъективное ощущение одиночества и другие социально-психологические особенности личности.
Исследование анонимное(при желании в конце исследования можно оставить свой E-mail, и мы отправим Вам результаты!)
Для исследования важно посмотреть более 1000 человек🙏🏻
Прошу помощи в распространении исследования между реальными и виртуальными знакомыми!❤️
Благодарю за помощь!!!
Каждый голос для меня важен 🤍🌿
Показать полностью
2
Подготовка творчески-одарённых профессиональных математиков по проекту А.Н. Колмогорова
Данная статья относится к Категории: Творческое развитие юношей и девушек
«В 1963 году при Московском, Ленинградском, Новосибирском и Киевском университетах по постановлению Совета Министров СССР одновременно были открыты четыре физико-математические школы-интерната. Создание школы-интерната при МГУ - школы нового типа - неразрывно связано, а теперь, с 1989 года, и официально, с именем А.Н. Колмогорова (хотя все и всегда называли её колмогоровский интернат, колмогоровская школа). Отвечая на вопрос о том, как он представляет себе первые шаги приобщения к науке будущего ученого. Андрей Николаевич писал:
«Прослеживая биографии известных учёных, в большинстве случаев в начале их пути мы найдём увлекшего наукой школьного учителя, обратившего на способного ученика индивидуальное внимание, первого научного руководителя, указавшего подходящую тему самостоятельного исследования, часто обдуманно приспособленную к возможностям именно данного студента. Часто заметим мы и одного или нескольких близких друзей-сверстников, поддерживающих друг друга. Думаю, что эти тонкие человеческие взаимоотношения, формирующие будущего ученого, сохранят все свое значение и в будущем. […]
Следуя этим принципам, Андрей Николаевич с первого дня создания своей физико-математической школы-интерната рассматривал непосредственно личную работу со школьниками, а затем и работу в более широком плане, связанную с совершенствованием содержания математического образования в средней школе в целом, как важную и нужную стране, как свою гражданскую ответственность за математическое просвещение.
В течение пятнадцати лет (!) он не только читает лекции и сам проводит упражнения для школьников, но и пишет для учащихся конспекты своих лекций, рассказывает им о музыке, живописи, архитектуре, литературе, ходит с ними в туристические походы, а летом проводит «выездные школы» для набора новых учащихся».
Ширяев А.Н., Жизнь и творчество. Биографический очерк, в Сб.: Колмогоров А.Н., Юбилейное издание в 3-х книгах. Книга первая. Истина – благо. Биобиблиография, М., «Физматлит», 2003 г., с. 160-161.
В 1964 году А.Н. Колмогоров написал свои соображения о подготовке профессиональных математиков:
«1. Вопрос, мне кажется, распадается на два:
а) Как добиться, чтобы из университетов выходило возможно больше творчески одарённых математикой, способных самостоятельно получать ценные для развития науки результаты и в будущем руководить подготовкой научных работников (быть хорошими руководителями дипломников и аспирантов).
б) Как добиться, чтобы большинство кончающих университеты (МГУ выпускает ежегодно 250 математиков) получили всю ту подготовку, которая необходима для той деятельности, к которой они предназначены.
2. Мне кажется, что для сколь угодно одарённых математиков полезно в студенческие годы находиться в коллективе, в котором имеют ясные представления о необходимом для всех уровне знаний и тренировки.
3. Фактически рядовой деятельностью кончивших математическое отделение МГУ является не только работа в НИИ (открытых или закрытых), но и работа ассистентов высшей технической школы и втузов. При развитии средних школ с увеличенным преподаванием математики и в них откроется важное поле деятельности наших выпускников. Фактически спрос на математиков со стороны научно-технических институтов отчасти объясняется тем, что значительная часть попавших туда математиков там не удерживается, а сбегает на работу ассистентов высшей школы. Положение улучшилось бы, если бы это обстоятельство было открыто признано и перед нашим факультетом была бы явно поставлена в качестве одной из задач подготовка ассистентов высшей школы.
4. Осуществить ... при приёме в университеты что-либо подобное отбору учеников Высшей Нормальной Школы (Парижская Ecole Normale Superieure - Прим. И.Л. Викентьева) нельзя и, вероятно, совсем не нужно. И в семнадцать, и в девятнадцать лет отделение «талантов» от будущих рядовых работников НИИ и ассистентов вузов кажется бесцельным, а вероятно, и вредным. Если считать желательным, чтобы в Московском университете процент действительно одарённых математиков был выше, чем он может быть при условии их выделения из обширного (250 человек) и, неизбежно, несколько случайного набора, то следует установить порядок перевода человек пятидесяти из других университетов на 3-4 курс. Если бы этот перевод был связан с обязательством по окончании университета или аспирантуры вернуться в вузы или НИИ той области, из которой переведённый приехал, то это было бы правильно. Конкурировать в нашу аспирантуру такие студенты, конечно, должны свободно».
Ширяев А.Н., Жизнь и творчество. Биографический очерк, в Сб.: Колмогоров А.Н., Юбилейное издание в 3-х книгах. Книга первая. Истина – благо. Биобиблиография, М., «Физматлит», 2003 г., с. 165-166.
Дополнительные материалы
+ Плейлист из 8-ми видео:
+ Ваши дополнительные возможности:
Идёт приём Ваших новых вопросов по более чем 400-м направлениям творческой деятельности – на онлайн-консультацию № 279 20 марта 2022 года (Воскресенье) в 19:59 (мск). Это принципиально бесплатный формат.
Задать вопросы Вы свободно можете здесь: https://vikent.ru/w0/
Изображения в статье
Андрей Николаевич Колмогоров — русский математик, создатель своей математической школы. Инициатор создания системы физико-математического образования для одарённых школьников / Источник фото & Изображение chenspec с сайта Pixabay
Андрей Колмогоров в гостях у учащихся физико-математической школы-интерната в Москве / T&P
Показать полностью
2
1
Ответ HitryFox в «Ловите математика!»2
Ну тут, к сожалению, товарищ @HitryFox немного фигню погнал =)
Итак, у нас есть ряд:
1998=3*666 (в 10-ричной системе)
1998=4*666 (в 16-ричной системе)
1998=5*666 (в 22-ричной системе)
1998=6*666 (в 28-ричной системе)
Достаточно просто взять калькулятор и проверить, что, например:
1998 = 7 * 666 (в 34-ричной системе счисления) - т.е. ряд можно продолжить
Изначально рассуждения HitryFox про значения многочлена были, конечно, верные, но вот насчёт 4 точек, лежащих на прямой, - уже что-то странное.
Во-первых, не стоит забывать, что в каждой строке это "666" указано в своей системе счисления, а поэтому это не арифметическая прогрессия.
Во-вторых, конечно же, многочлен n-ной степени может иметь с прямой не более чем n пересечений (а не n+1). Желающие могут вывести это, чуть пошатав основную теорему алгебры при помощи вращения координат.
Так что же тут происходит на самом деле? Действительно 1998 в x-ричной системе счисления - это значение многочлена P(x) = x^3 + 9x^2 + 9x + 8.
Аналогично, 666 (в x-ричной системе) - значение многочлена Q(x) = 6x^2 + 6x + 6.
Значения уже считаем в нашей нормальной 10-тичной системе.
Итого, глядя на ряд, у нас получается гипотеза:
Для любого натурального а >= 3 выполняется: P(6a - 8) = a * Q(6a - 8)
Как проверить, верно ли это? Ну... Желающие просто могут раскрыть скобки)
Почему а >= 3? Чтобы соображения о системе счисления имели смысл (ведь в 4-ричной системе уже не существует числа 1998).
А так-то, конечно, a может быть вообще любым, хоть комплексным. Добро пожаловать в удивительный мир делимости многочленов =)
Показать полностью