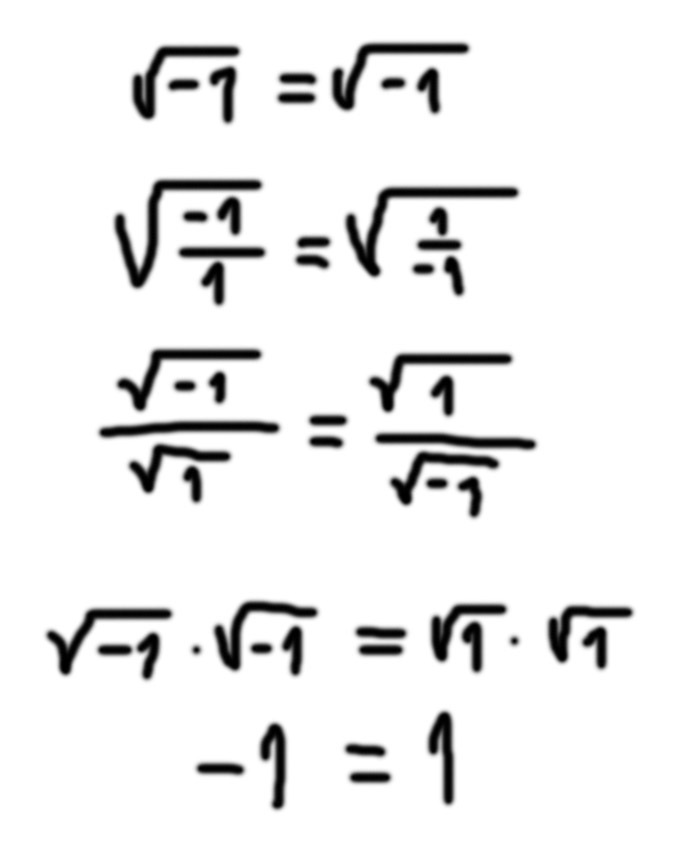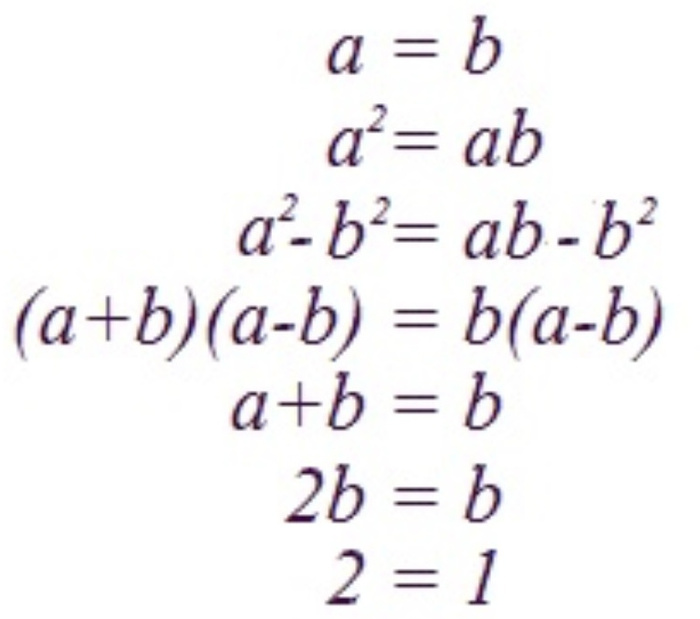Эффект «ты не идиот»: как простая фраза заставляет людей доказывать обратное
Иногда люди могут заблуждаться даже в элементарных вещах. Например, в математике.
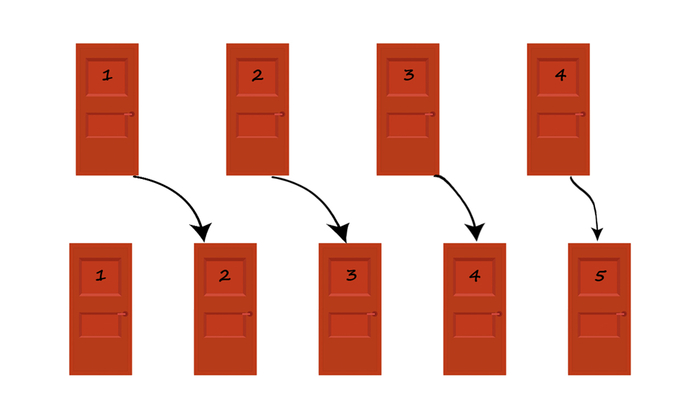
Многие считают 1+1=2 и никак иначе.
На самом деле:
1+1=1 - это булевая алгебра, дизъюнкция. (Правильнее записывать 1 v 1 = 1)
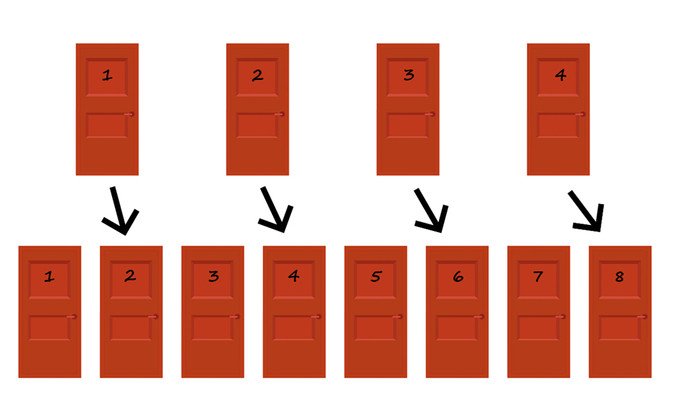
1+1=10 - это двоичная логика (арифметическое сложение в двоичной системе счисления). Есть 10 типа людей - кто понимает двоичную логику и кто не понимает.
1+1=0 - это побитовое сложение с переполнением регистра без переноса. Сложение по модулю 2. "Один в уме" - это как раз перенос, который реализовывается отдельной логикой*.
1+1=11 - это конкатенация (преимущественно для языков программирования, там "+" перегружен на поддержку объединения последовательностей).
1+1=2 - это арифметическое сложение в системах счисления, чье основание равно 3** и больше. Для арифметического сложения в разных системах счисления 1+1=10_2 и 1+1=2_10 эквиваленты. 10_2 - 10 с нижним индексом 2, 2_10 - 2 с нижним индексом 10. Нижний индекс определяет основание системы счисления. Для человека по умолчанию считается нижний индекс равный 10, для компьютера нижний индекс равен двум, поэтому в специализированной литературе нижние индексы могут не записываться.
*) отдельная логика сумматоров, если кратко: сложение двух бит _a_ и _b_ определяется набором: старший бит _с_=_a_*_b_ (двоичное И), младший бит (_a_ xor _b_). Это получен полусумматор. Только вот второй разряд _c_ (один или ноль в уме) нужно прибавить к соответствующим _a_ и _b_ следующего разряда, поэтому сложение реализовывается для трех разрядов - a,b и перенос с предыдущего разряда или два полусумматора дают один сумматор.
**)Не все виды троичной системы счисления подходят, т.к. там есть сбалансированный вариант троичной системы вида (-1, 0, 1), соответственно, двойки в ответе не будет (визуально не будет, по смыслу она там будет и будет записана иначе).
Люди могут плохо знать такие нюансы математики, что она не ограничивается арифметикой. Арифметика - это лишь один из разделов математики. Математика включает и другие разделы: булевая алгебра, теория графов, теория множеств, статистика, дифферинциальное исчисление и т.д. Либо быть просто дурачками по жизни.
Я склоняюсь к первому варианту, что люди просто не знают и их можно просвятить. Что мир сложнее, чем написано в школьном учебнике за первый класс. Но почему люди достаточно часто пытаются доказать, что я ошибаюсь и на самом деле они относятся ко второй группе? Как будто такие люди родились в семье двух таксистов, которые тайно правят миром не привлекая внимание психиатров.
- Фрукт - фрукт, сиська - сиська, цветок - цветок, тоже самое, мать твою.
- Да, капитан, они довольно похожи. (...) [Первая картина - работа известного художника]. А [вторая картина] просто мерзость.
Заметили? "Эксперт по одинаковости картин" находится в звании капитана! У него действительно может быть маленький [пиратский?] бизнес и он действительно управляет крупной организацией - командой корабля. И он действительно может повлиять на мир, убивая ученых и важных персон.
"Миром правит не тайная ложа, а явная лажа" (с) Пелевин