Как люди научились считать?
Когда мы говорим «люди научились считать», это подразумевает, что когда-то очень давно люди считать совсем не умели. Но так ли это? Исследования биологов показали, что не совсем так, если не сказать – совсем не так.
Начнём... с растений! Да-да, с растений! В Северной Америке, а именно в штатах Северная и Южная Каролина, на болотах произрастает удивительное растение – венерина мухоловка. Помните песенку про кузнечика – «он ел одну лишь травку и с мухами дружил...» и так далее? Так вот, эта «травка» ест кузнечиков. И муравьёв, и мух, и гусениц тоже.
Листья венериной мухоловки – самые настоящие капканы с острыми зубами по краям. Когда растение охотится, оно широко раскрывает свои ярко окрашенные изнутри листья – дескать, «приходите, тараканы, я вас чаем (в смысле нектаром) угощу...». Только горе той мухе-цокотухе, которая решит зайти к мухоловке «на чай». Лист-капкан очень быстро захлопывается, и насекомое оказывается в смертельной ловушке. Дальше лист выделяет пищеварительный сок, растворяет добычу и выпивает досуха. Когда лист мухоловки снова раскроется, от насекомого останется только хитиновая шкурка, которую унесёт ветер...
Учёные задались вопросом: как мухоловка определяет, что на лист уселась добыча? Сперва ответ казался очевидным: на внутренней поверхности листа у мухоловки есть множество чувствительных волосков. Дотронулся кузнечик до волоска – и волосок как бы посылает мухоловке сигнал: «Хватай!». Но... более внимательные наблюдения показали очень странную вещь: чувствительные волоски мухоловки совершенно не реагировали на посторонние объекты. Например, на случайно упавшую веточку. Или кусочек мусора. Или даже на дождевую каплю! Будто бы у мухоловки есть глаза, и она видит – что именно попало в ловушку. Как в игре «съедобное-несъедобное» (играли?).
Что же открыли биологи? Опыты показали, что у венериной мухоловки нет глаз, зато она... умеет считать! Вот на волосок листа мухоловки упала соринка – РАЗ. Мухоловка ждёт – дальше ничего не происходит? Нет. Тогда не дёргаемся, продолжаем охоту, тревога ложная. Но вот на лист прыгнул тот самый кузнечик. Он задел один волосок (РАЗ), другой (ДВА), третий (ТРИ) – хлоп! Лист-капкан захлопывается. Но это ещё не всё – вдруг всё-таки произошла ошибка? И мухоловка терпеливо ждёт: пойманный кузнечик начинает трепыхаться, пытается вырваться из ловушки, снова задевает волоски – ЧЕТЫРЕ и ПЯТЬ. На пятом касании растение окончательно убеждается: в ловушке – обед! И только после этого выпускает пищеварительные соки.
И тогда биологи задумались: уж если даже некоторые растения умеют считать до пяти, то что же тогда животные? Ведь поведение животных в большинстве случаев намного сложнее поведения растений... Когда знаешь, где и что искать, результат обычно находится довольно быстро. Опыты с обезьянами-шимпанзе показали, что те умеют не только считать, но и решать в уме простые примеры на сложение!
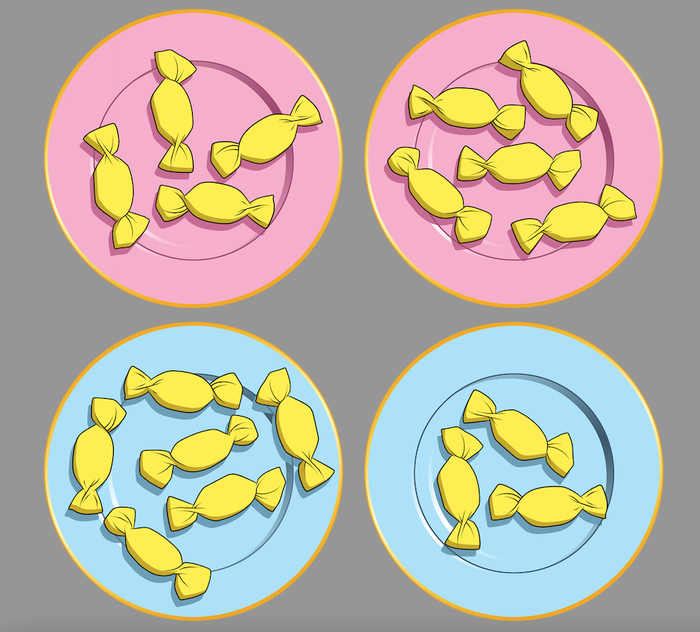
Обезьянам предлагали на выбор две пары тарелочек с конфетами (можно было выбрать одну пару), причём количество конфет в каждой тарелочке было разное. Так вот – шимпанзе почти безошибочно (9 правильных ответов из 10) выбирали именно ту пару тарелочек, на которой сумма конфет была больше!
Представьте, что надо "на глазок", не считая, определить, где конфет больше – на розовых тарелках или на голубых? И не ошибиться девять раз из десяти (комбинации конфет будут разные). Как думаете, получится у вас это сделать, не считая?
Думаете, это всё? Если бы! Оказалось, что отлично умеют считать волки и львы! Когда на территорию одной волчьей стаи вторгалась другая волчья стая, волки, внимательно слушая вой («голоса») чужаков, всегда знали, сколько волков в чужой стае, больше или меньше. Если меньше, волки атаковали пришельцев. Если же «чужих» было больше, стая уступала им территорию без боя.
Точно такое же поведение демонстрировали прайды львов – львы считали голоса чужаков, сравнивали количество «сколько нас» и «сколько их», и делали абсолютно правильные выводы.
Однако волки, обезьяны и львы – всё-таки высшие животные. А как насчёт насекомых?
И снова результаты опытов озадачили учёных: оказалось, что обыкновенные медоносные пчёлы прекрасно умеют считать до четырёх!
Как это выяснили? С помощью опыта: пчёл запускали в лабиринт с двумя комнатками. В одной комнатке стояла мисочка с мёдом, вторая комнатка была пустой. Пути в разные комнаты исследователи отмечали последовательностями из крупных и ярких геометрических фигур: треугольник, круг, квадрат... Выяснилось, что, когда таких меток на правильном пути было одна, две, три или четыре, пчёлы безошибочно запоминали правильный путь. Но вот когда меток на каждом пути становилось больше, пчёлы начали ошибаться и прилетать в пустую комнату так же часто, как в комнату с кормом... То есть пчёлы умеют считать!
Но ведь их никто этому не учит! Выходит, навыки счёта животные получают просто «от природы»?
Как это происходит? На эту тему учёные высказывают самые разные гипотезы – но единого и стопроцентно верного решения пока что не нашлось. Одна из самых распространённых гипотез говорит о том, что числа у животных и человека возникают в процессе нервной деятельности в головном мозге (а даже у медоносной пчелы есть головной мозг, представьте себе!) как бы «автоматически». Смотрите.
Самое первое (и главное!) природное число – это «один». Что такое «один»? Представьте себе: летний полдень, пасека, ульи, над поляной с цветами жужжит множество пчёл, собирающих нектар. А в стороне, на ветке деревца, притаился в засаде хищник – оса-филант, которую пчеловоды называют «пчелиный волк». Пока пчёлы летают дружно, роем, пока их «много», они опасны! Филант терпеливо ждёт, сидит неподвижно и пристально наблюдает. Но вот одна из пчёл неосторожно отлетела от подружек в сторону, осталась «одна»! Филант видит эту ОДНУ пчелу и молниеносно бросается на неё!
Понимаете, насколько важно для охотника понимать разницу между «один» и «много»? Если бы филант этого не понимал, он бы запросто сунулся в гущу пчёл, те с воплями «наших бьют!» накинулись бы на него коллективно, и закончилось бы это для филанта грустнее некуда.
Второе природное число – это число «два». В муравейнике голодный муравей выпрашивает у сытого собрата каплю еды – это взаимоотношение «я и ты», «я и партнёр». Точно так же обмениваются кормом осы и пчёлы. Число «два» – это мать и детёныш. Ну и, само собой, не забываем, что у человека две руки, две ноги, два глаза, два уха – эти открытия малыш тоже осознаёт и «принимает к сведению».
Наконец, в мозгу у живого существа постепенно появляется и природное число «три». Число «три» – это как бы окно во внешний мир, это «я, ты и кто-то ещё». Например, «я, моя добыча и враг, который хочет эту добычу у меня отобрать». Или «я, хищник, который на меня охотится, и спасительная нора».
Числа «один, два, три» в восприятии живых существ – невероятно древние, им десятки миллионов лет. Недаром эти числа у людей всегда считались самыми главными, самыми волшебными и магическими. У кого есть второй номер «Лучика» за 2022 год? Вспоминайте статьи «Почему Бог троицу любит?» и «Троичная логика!».
Постепенно, очень медленно, формируются представления о более сложных числах: четыре лапы у кошки, пять пальцев на одной руке. Это было непросто! Вы уже читали книжку про Робинзона Крузо? Помните, там моряк Робинзон подружился с краснокожим туземцем по имени Пятница? Как Пятница считал? «Раз, два, три, много». Если Пятница хотел назвать число «пять», он говорил: «Раз, два, три, раз, два». А если число «шесть» – то: «Раз, два, три, раз, два, три».
Для большинства животных числа «пять» и «шесть» – это уже «чересчур». Тут (за редким исключением) справляются только люди. Опыты показывают, что чем число больше, тем труднее с ним работать животным, и в какой-то момент все большие числа у них превращаются в неопределённое «много».
Собака хорошо различает два удара стенных часов («время обедать!) и семь ударов часов («время гулять!»), но вот девять часов от десяти отличает очень плохо.
Обезьяна сумеет отличить двадцать конфет от шестидесяти конфет (то есть она понимает, что одно «много» может быть больше другого «много»). Но вот отличить двадцать две конфеты от двадцати трёх обезьяна уже не сумеет.
Существует и другое важное отличие людей от животных – в том, как они воспринимают числа. Опыты показали, что животные (и примитивные люди!) не умеют мыслить числами абстрактно, отвлечённо. Кошка прекрасно отличает одну мышку от двух мышек – но она не понимает существования самого числа два.
Учёные, которые изучали жизнь человеческих племён, ведущих естественный образ жизни (примерно таких, как тот самый Пятница из книжки), очень удивлялись такому факту: эти люди часто умели считать, но при этом они умели считать только предметы, причём только одинаковые предметы!
Например, говорят такому человеку:
– Пожалуйста, посчитай до десяти на своём языке! – Хорошо. А что посчитать? – спрашивает тот. – Ничего. Просто посчитай!
И человек очень удивляется. Как же можно посчитать то, чего нет? Такой человек мог считать только «один орех, два ореха...» или «одна лодка, две лодки...», но посчитать «один, два» он не мог!
Или, например, ему говорят: «Здесь растёт шесть пальм».
А он: «Здесь нет шести пальм! Есть три банановые пальмы, две кокосовые и одна саговая. И всё!»
Как можно складывать кокосовые пальмы с банановыми?
Не спешите, кстати, смеяться над «глупым дикарём». В его рассуждениях есть здравый смысл! И сами мы, когда учимся в школе арифметике, делаем множество ошибок, когда вдруг начинаем во время решения задач, например, складывать «метры с секундами». Понимание того, что можно складывать друг с другом (и умножать, и делить), а что нельзя, – это довольно хитрая штука, которой дети обучаются в школе не один год. И островитянин, который говорит, что кокосовые пальмы нельзя складывать с банановыми, по-своему прав. Просто у него ещё не развилось «абстрактное мышление».
Как у Буратино, помните?
– Я говорю, – терпеливо повторила девочка, – предположим, что у вас в кармане два яблока. Некто взял у вас одно яблоко. Сколько у вас осталось яблок? – Два. – Подумайте хорошенько. Буратино сморщился – так здорово подумал. – Два... – Почему? – Я же не отдам Некту яблоко, хоть он дерись! – У вас нет никаких способностей к математике, – с огорчением сказала девочка. – Займёмся диктантом.
Абстрактному мышлению («яблоки вообще», «пальмы вообще») люди научились не так уж давно – приблизительно пять-шесть тысяч лет назад. «Как подсчитать, сколько будет десять цыплят и пять цыплят?» – строго спрашивал учитель ученика в школе в Древнем Египте. Ученик отсчитывал десять палочек, затем ещё пять палочек, считал палочки вместе – и гордо отвечал: «Будет пятнадцать цыплят!». Он считал палочки, а отвечал «в цыплятах» – и это было величайшее открытие древней математики.
Вы читали журнал "Лучик".