bayesyatina

Радикальный скептик (Далее Р): О, привет. Ты же развиваешь критическое мышление?

Сайнстер (далее С): Да, конечно!

Р: Отлично. А ты знаешь, что сепульки существуют?

С: Ха. Специально для подобных утверждений существует Бритва Хитченса. Этот принцип, который изобрёл известный научный скептик Кристофер Хитченс, и гласит он: то, что заявляется без доказательств, может быть отвергнуто без доказательств.

Р: Как же вы любите апеллировать к авторитетам. Но, так чисто для справки, Хитченс ничего не изобретал, а просто пересказал широко используемую ещё с XIX века латинскую пословицу «Quod gratis asseritur, gratis negatur» («Что свободно утверждается, то свободно отбрасывается»). Поэтому я бы не сказал, что он прям изобрёл новый гносеологический принцип. Но давай по существу: я отклоняю бритву Хитченса на основании бритвы Хитченса. Ты заявил этот принцип без доказательств, и я отклоняю его без доказательств.

С: Эй, это не так работает! Тебе знаком термин бремя доказательств? Бремя доказательств лежит на том, кто что-то утверждает! Ты выдвинул утверждение о существовании сепулек, значит, ты и обязан приводить доказательства.

Р: Это очень скользкое правило. Был такой философ Ричард Уэтли, так вот он в своих работах сравнивал подобные стратегии с гарнизоном, обороняющим осаждённый форт. Форт может быть неприступен, пока гарнизон ведёт оборонительную игру, но если командир решит совершить вылазку в открытое поле, поражение может последовать незамедлительно. Так и в споре человеку достаточно только скептических аргументов, чтобы успешно отстаивать свою позицию. Поэтому крайне выгодны стратегии, перекладывающие на оппонента, необходимость выдвигать утверждения. Проблема в том, что почти любое предложение в естественном языке можно переформулировать в негативной форме. Вот смотри: ты утверждаешь, что сепулек нет, значит, бремя доказательств на тебе. Я-то ничего не утверждаю, а лишь скептически отношусь к подобному твоему УТВЕРЖДЕНИЮ. Скажи-ка мне, ты точно везде проверял отсутствие сепулек? Покажи мне мета-анализы, эксперименты, или что ты там используешь в качестве доказательств?

С: Погоди, я же ничего не утверждал.

Р: А, ну вот мы и выяснили, что ты не отрицаешь существования сепулек? Ну, значит, ты согласен, что они существуют.

С: Пфф. Ты просто совершаешь классическую логическую ошибку, о которой писал ещё Джон Локк. Её название Argumentum ad ignorantiam - аргумент к невежеству. Это аргументы вида: Привидения существуют, поскольку никто ещё не доказал, что их нет.

Р: Как же вы любите ссылаться на философов, при этом называя философию бесполезной. Но я, кажется, уловил суть. Нельзя делать выводы из отсутствия свидетельств, так?

С: Ну наконец-то ты понял.

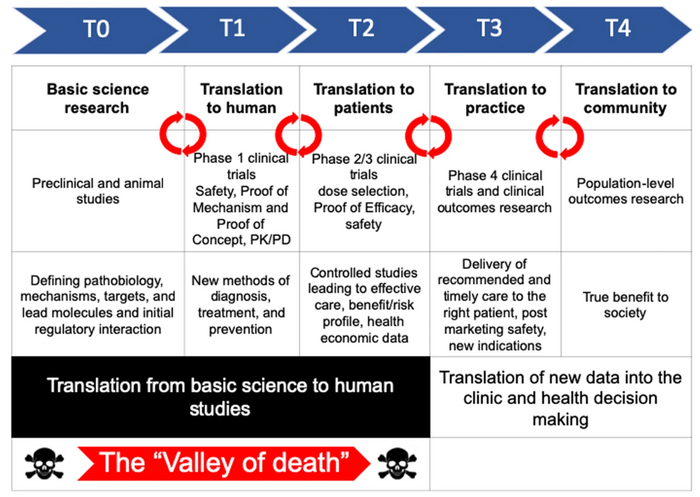
Р: То есть мы не можем сделать вывод о безопасности препарата из того факта, что мы не обнаружили побочные эффекты?

С: Хм…

Б: Если бы сайнстер прочитал статью про логические ошибки, то, вероятно, он бы узнал, что они делятся на формальные и неформальные. Последние, к которым и относится аргумент к невежеству, зачастую вообще не являются ошибками.

С: Ты кто?

Б: Меня зовут Роман Ачисов, вы, кстати, читаете какую-то байесятину, и мы здесь пытаемся меньше ошибаться. Иногда отсутствие свидетельств что-то доказывает, а иногда нет. Например, когда речь идёт о лекарстве, мы считаем препарат безопасным, если в исследованиях не нашли побочных эффектов. Но при этом мы не считаем, что призраки существуют только потому, что у нас нет доказательств обратного. Почему так? Здесь нам поможет немного Байесовской магии.

Когда мы получаем какое-то свидетельство, оно изменяет вероятности гипотез. Гипотезы, при которых такое свидетельство было более ожидаемым, становятся вероятнее, а гипотезы, при которых оно маловероятно, наоборот, теряют вес. Это напоминает весы: если одна чаша опускается, другая поднимается.

Допустим, у нас есть две гипотезы:

• Г1: препарат безопасен (то есть у него нет ни одной побочки)

• Г2: препарат опасен, но его побочные эффекты очень редки и могут не проявиться в исследовании

Эти гипотезы представляют собой два мира, в которых мы можем жить (строгости ради их гораздо больше). И вот мы проводим исследование и не находим побочек. Означает ли это, что лекарство безопасно? Не совсем. Мы могли ожидать такой результат при обеих гипотезах. Именно в этот момент многие восклицают: отсутствие свидетельств - это не свидетельство отсутствия. Но с точки зрения теория вероятностей, наши шансы получить такой результат чуть выше, при Г1 (безопасное лекарство). То есть в первом мире такой результат был бы чуть более вероятным. Значит, наше доверие к Г1 немного растёт, но не слишком сильно.

Если бы Г2 предполагала, что побочки очень частые, то отсутствие их в исследовании стало бы уже сильным свидетельством против неё. Чем больше раз мы повторяем тест (исследование) и не находим побочек, тем сильнее наше доверие к гипотезе о безопасности.

При этом важно учитывать не только количество исследований, но и их качество (например, насколько тесты чувствительны), но это мы обсудим в другой раз.

Сейчас я лишь хочу подчеркнуть, что отсутствие свидетельств вообще-то может быть аргументом, но сила этого аргумента определяется тем, с какой вероятностью мы ожидаем различных исходов при разных гипотезах. В мире, где существуют приведения, но они хорошо прячутся, шансы встретить их не высокие. Но в мире где их не существует, шансы ещё ниже. И если мы не встретили их, или не нашли в результате эксперимента, то это нормальный аргумент в пользу их отсутствия.

[Если хотите больше "технических" подробностей, то читайте эту работу]

Р: Ну допустим, отсутствие доказательств существования сепулек является слабым свидетельством в пользу того, что они не существуют. Я согласен с такой формулировкой. Но мы тут, вообще-то, бремя доказательств перекидываем, если ты не заметил. На ком же оно?

С: Конечно, на тебе. Даже без логических ошибок, бремя доказательств падает на того, кто утверждает что-то необычное. А существование сепулек определённо необычное заявление! Как сказал Карл Саган, экстраординарные утверждения требуют экстраординарных доказательств.

Р: Ну, вообще-то, ни сам принцип, ни даже эта формулировка не принадлежат Сагану. Принцип впервые упомянул в своей работе философом Дэвид Юмом за 200 лет до него. Формулировку же в таком виде за несколько лет до Сагана озвучил социолог Марчелло Труцци.

С: Ты здорово уходишь от разговора, но со мной этой не прокатит. Бремя доказательств на тебе, потому что ты утверждаешь нечто отличное от нормы. Ты слышал про чайник Рассела? Если я скажу, что между Землёй и Марсом вращается фарфоровый чайник, слишком маленький, чтобы его могли обнаружить даже самые мощные телескопы, никто не сможет доказать, что я ошибаюсь. Но если я заявлю, что, поскольку никто не может опровергнуть моё утверждение, оно не должно подвергаться сомнению, я буду высмеян.

Р: Да, только позволь мне закончить эту цитату философа Бертрана Рассела, звучит она так: «Однако, если существование такого чайника было бы записано в древних книгах, преподано детям как священная истина и внушалось бы обществу с раннего возраста, сомнение в его существовании выглядело бы странным, а скептик подвергался бы осуждению». Как видишь, Рассел указывал на относительность понятия нормы. Вот в моём окружении большинство определённо верят в сепульки. И заявление, что их не существует не только глубоко возмутительно, но и крайне необычно.

С: Странное у тебя, конечно, окружение. Но к счастью, большинство людей в сепульки не верят. Так что тебе не увернуться от бремени доказательств.

Р: О, любитель неформальных логических ошибок прибегает к аргументу от большинства? То есть продажи гомеопатических препаратов подтверждают их работоспособность?

С: Ладно, ты прав. Мнение большинства не всегда надёжно. Но у нас же есть научный консенсус! Мнение профильных специалистов легко укажет на то, какое мнение сто́ит считать необычным, а стало быть, и на то, кто обязан предоставлять доказательства.

Р: Это резонное предложение. Вот только с ним связана пара проблем. Кого считать специалистами? Вот, например, в вопросе НЛО астрономы небезосновательно считают себя специалистами. Однако всякие там уфологи тоже претендуют на эту роль.

С: Ты что ещё и в НЛО веришь?

Р: Термин абстрактные рассуждения тебе, видимо, неизвестен. Нет, я просто сбиваю твою спесь и пафос. Ну вот есть этот ваш любимый научный метод. А кто является экспертами по нему? Физики, математики или социологи? Может, философы? А, как я мог забыть, философия же не наука.

С: Ну хорошо,не для всех вопросов есть очевидно подходящее сообщество экспертов, но для многих же есть?

Б: У меня была статья про авторитет. Там как раз поднимался вопрос того, кому стоит доверять и почему. Всё, что там было сказано, относится не только к отдельным авторитетам, но и к экспертным сообществам. На уровне сообществ также бывают конфликты интересов. То есть если вы спросите сообщество специалистов по сепулькам, существуют ли сепульки, то они будут иметь сильное давление ответить положительно. Это не значит, что их выводы можно выкинуть в мусорку, но это стоит учитывать наряду с другими свидетельствами. Ещё одной важной тонкостью будет то, что консенсус будет тем более точен, чем более независимы мнения экспертов внутри него. Если все эксперты воспитаны в рамках «одной школы», это создаёт эхо-камеру. Основная суть в том, что разные сообщества заслуживают разной степени доверия.

Р: Ну в такой формулировке я не спорю с рекомендацией оттолкнуться от консенсусного мнения.

С: Получается бремя доказательств на тебе?

Р: Почему?

С: Ну ведь научный консенсус на моей стороне?

Р: А с чего ты это взял?

С: То есть ты думаешь, большинство учёных считают, что сепульки есть?

Р: Каких именно учёных?

С: Да какая разница?

Р: Огромная. Вот ты утверждаешь, что бремя на мне, потому что таков научный консенсус. А сам не удосужился даже проверить есть ли подобные опросы или что пишут в учебниках. В чём сила твоего аргумента, если ты просто говоришь: я верю, что учёные считают так, значит, я прав? Такой подход называется критическим мышлением? Я просто не в курсе.

С: Я так устал от твоей бесполезной демагогии.

Р: Вот так всегда, как только у тебя заканчиваются аргументы, ты объявляешь меня софистом и демагогом. Это ни разу не ad hominem, здесь никаких норм рационального диспута не нарушается.

С: Пусть нас рассудит третья сторона: на ком должно быть бремя доказательств?

Б: Ну вообще ни на ком.

С: В смысле?

Б: Дело в том, что средневековый диспут заимствовал общие нормы римского права, среди которых была идея о том, что бремя доказательства лежит на утверждающем. Оттуда концепция распространилась на руководства по проведению дебатов и теоретические работы по риторике и аргументации, а после популяризовано и, так сказать, ушло в массы. Однако это заимствование не очень уместно. Если целью спора является совместный поиск истины (или более практически наилучшей позиции с обоснованной степенью уверенности), то лучшей стратегией будет просто вывалить на стол лучшие аргументы, перемешать их с аргументами собеседника и взвесить чаши весов. Вообще, крутым лайфхаком для рационального спора является вести обсуждение так, как делал бы это наедине с собой. Ну правда, почему должна быть какая-то разница между самостоятельным рассуждением над темой и диалогом, если цель в установлении истины?

С: А что если собеседник не хочет вести нормальный спор? Как мне его заставить? Вот в чём главный вопрос!

Б: Я считаю - это довольно вредная интуиция, что есть объективные стандарты спора, и если собеседник их не выполняет, то можно принудить его к этому. Отсюда и берётся вся эпопея со списками логических ошибок. У каждого человека есть личные эпистемические стандарты. Я вот считаю, что полезно использовать в некоторых рассуждениях логику и теорию вероятности. Более того, я верю в то, что есть более эффективные познавательные стратегии (эпистемическая нормативность) к обладанию которыми я и стремлюсь. Если у другого человека стандарты отличаются, вам придётся придумать формат в котором вы сможете взаимполезно обмениваться информацией не соблюдая эпистемические стандарты друг друга. Ну или прийти к общим стандартам (что вообще-то отдельная задача).

Р: Погоди, то есть бремя доказательств по-твоему бесполезно? А ничего, что это юридический термин?

Б: Бремя доказательств — это важная штука, но работает она не везде. Вот в этой работе авторы делят споры на два типа: в одном бремя доказательств только мешает, а в другом — наоборот, необходимо.

Когда спор касается просто установления истины или оценки степени уверенности (то есть, насколько вероятно, что что-то, правда), здесь перекидывание бремени доказательств только мешает. Но есть и споры, где мы не просто ищем истину, а решаем, что с ней делать — и это решение несёт за собой риски и последствия. Например, если мы уверены в чём-то на 70% (ну, к примеру, в безопасности препарата), и мы должны решить: когда стоит действовать (например выпускать его на рынок или нет)? Для таких случаев нужна граница принятия решений. Такие споры называют пруденциальными, потому что здесь важно учитывать риски.

Классический пример — юридическая система. В уголовном праве презумпция невиновности специально создаёт перекос в пользу обвиняемого. Это потому, что наказать невиновного считается гораздо хуже, чем отпустить виновного. С точки зрения поиска истины — да, это искажение и подкручивание. Но с точки зрения принятия решений это оправдано, потому что в долгосрочной перспективе даёт наилучший результат.

Это применимо не только в судах. Бремя доказательств нужно в любой ситуации, где ошибиться в одну сторону хуже, чем в другую. Это называют пруденциальной асимметрией.

Яркий пример из другой сферы, это история с талидомидом. В 1950-х этот препарат активно продвигали как средство от тошноты у беременных. В результате более 10 000 детей родились с тяжёлыми пороками развития, а около 40% из них не выжили.

Но в США лекарство так и не попало на рынок благодаря сотруднице FDA Фрэнсис Келси. Она отказалась одобрять таледомид, потому что на её (субъективный) взгляд доказательств безопасности не достаточно. Этот случай изменил систему регулирования лекарств и принёс Келси президентскую награду.

В жизни мы тоже интуитивно сдвигаем бремя доказательств в подобных ситуациях. Представь, ты берёшь в руки охотничье ружьё. Разумнее считать, что оно заряжено, пока не убедишься в обратном. А вот если ты берёшь банку газировки, логично предполагать, что она не взболтана, пока нет оснований считать иначе.

Конечно, правильно установить бремя доказательств в споре с пруденциальной асимметрией очень сложно и трудозатратно. Есть высокий риск промахнуться, и устанавливащий несёт серьёзную ответственность за последствия. Но в этом случае это неизбежно.

Совершенно другая ситуация в бытовых спорах. Бремя доказательств в них всплывает из интуиции о внешнем судье. Как будто существуют объективные стандарты (не этические), которых необходимо придерживаться в дебатах. И один из них заключается в том, что пока оппонент строго не доказал что-то, вас этот внешний судья признаёт правым. Мол, вы имеете полное право верить в любые убеждения, пока не получили идеальное математическое доказательство своей неправоты. Как я уже говорил в одном из роликов, это наследие аристотелевской логики, в которой ты либо точно прав, либо также точно ошибаешься. Именно в такой ситуации очень важно, кто будет утверждать, ведь, как верно заметил радикальный скептик, гораздо проще указать на ошибки, чем создать идеальную и безошибочную концепцию.

Я же предлагаю байесовскую перспективу, где у тебя и собеседника есть некоторые обоснованные степени уверенности. Обоснованы они доказательствами. И целью спора является вывалить всё свои доказательства на стол, и совместно взвесить. В этом случае бремя доказательств становится обременительно для обеих сторон. Это, конечно, не сделает любое обсуждение идеальным, особенно если собеседник не поддерживает такой подход. Но даже в одностороннем порядке это может увеличить лично вашу пользу от такого диалога.

С: Ну звучит здраво. Но что там с сепульками?

Р: Ой, да нет никаких сепулек. Я просто хотел поспорить. Пошли чай пить.

Ситуация в гарантийном центре по обслуживанию убеждений.

• Здравствуйте! Я хотел бы вернуть пару убеждений по гарантии.

• Добрый день! Давайте посмотрим. Где приобретали?

• Ну вот это ещё в школе, кажется, брал, а это из книжки.

• А это что? (Указывая на прилипшее к руке убеждение)

• А, это из группового чата. Теория заговора про злобных англосаксов. Прилипла, не могу отодрать.

• Давайте помогу (приставляет книжку Роба Бразертона “Недоверчивые умы”, убеждение с шипением отлетает). Ну смотрите, такое (указывая на отлетевшее убеждение) мы не обслуживаем. На это, школьное, срок годности вышел. А вот это давайте посмотрим. Вроде нормально всё. А в чём проблема?

• Не работает. Ну как не работает, ожидания не оправдывает.

• (недолго крутит в руках убеждение и светит фонариком) Ааа, понятно. Так вы в нём слишком уверены. Убеждением нормальное, вы в нём просто не сомневаетесь совсем. Про калибровку уверенности слышали?

• Нет, а что это.

• Оно и видно. Как зовут вас?

• Гриша. И давай на ты?

• Хорошо, пойдём

• Куда?

• В твою голову. Куда же ещё.

(громкий хлопок, герои оказываются в месте, похожем на заваленный склад)

• Как я и думал. Бардачок тут у тебя. Ничего, разберёшь. Был такой когнитивный психолог, Даниель Канеман, так вот он однажды сказал: «В жизни вашего разума есть одна примечательная особенность: вы редко приходите в замешательство». Канеман имел в виду, что мы редко сомневаемся в своих знаниях, и про любую тему рассуждаем с лёгкостью. У нас есть мнение почти обо всём. О, это что, велосипед?

• Да

• А ты знаешь, как он устроен?

• Ну да, я его тысячу раз видел

• Здорово, а сможешь его нарисовать?

• Ну я не художник

• Это не проверка художественных способностей, просто обозначь принципиально, как надо расположить детали, чтобы он работал.

• А, тогда легко. Взрослый же?

• Да, взрослый. Психолог Ребекка Лоусон предложила испытуемым сделать то же самое. Все испытуемые жили в городе и видели велосипеды постоянно, большинство умели водить велосипед, и у многих он даже стоял дома. И при этом больше половины испытуемых не справились. Причём не справились, это значит, допустили принципиальные ошибки, которые приводят к тому, что велосипед точно не будет работать, как задумано. Кто-то рисовал раму между передними и задними колёсами, что не позволяет поворачивать рулю. Кто-то рисует педали на переднем колесе, хотя в задании чётко оговаривался взрослый двухколёсный велосипед. Но большинство допустило ту же ошибку, что и Гриша. Нарисовали цепь между передними и задними колёсами.

• Похоже, я знаю меньше, чем казалось

• Точно так же сказал один из участников исследования. Очевидно, мы можем обойтись без подробных знаний об устройстве велосипеда. Здесь важно другое. До прохождения испытания Лоусон попросила оценить уровень понимания этого самого устройства по шкале от 1 до 7 (от "я не знаю вообще" до я "досконально знаю его устройство"). Средние оценки колебались между 4-5, то есть люди думали, что довольно неплохо знают, как устроен велосипед. Однако для многих это оказалось иллюзией, которая развеялась, только когда они заглянули в свой мозг и не нашли там нормальной конструкции. Оставлю тебе это на память.

• Что это?

• Художник Джанлука Джимини попросил друзей по памяти нарисовать велосипед, а потом воссоздал рисунки в 3д, чтобы они стали как настоящие.

• М-да, лучше бы ты мне нормальный чертёж дал.

• Проблема не в том, что ты чего-то не знаешь. Профессор Девид Даннинг объясняет это так: «Совершенно определённо, невежественный мозг нельзя сравнить с пустым сосудом. Он наполнен всякой накопленной за годы информацией: жизненным опытом, теориями, фактами, интуитивными догадками, стратегиями, алгоритмами, эвристическими правилами и метафорами». Нам нравится определённость, и хочется ощущать твёрдую почву под ногами. Однако зачастую это ощущение иллюзорно, а наши знания вовсе не так надёжны, как нам кажется. Посмотри, твой мозг имеет мнение по любому вопросу, и на первый взгляд они все кажутся надёжными. Но если ты взглянешь подробнее, окажется, что информация у тебя есть далеко не обо всём.

• Ну это понятно. Я не могу знать всего.

• Да, но это не мешает тебе одинаково уверенно рассуждать буквально обо всём, о чём ты имеешь хотя бы поверхностные знания. Учёные обнаружили, что люди особенно предрасположены к переоценке своих знаний в простых физических задачах (например: по какой траектории будет падать тело?) природных явлений (как возникает радуга и куда направлен хвост кометы?) и устройств (как работает застёжка-молния?), а также со сложными социальными структурами вроде политики или права.

• Ну, допустим. Но что плохого в том, чтобы быть слишком уверенным в подобных штуках? Ну самоуверен я в области политики, кому это мешает?

• О, проблема в том, что у тебя есть общее правило для сортировки всех твоих убеждений. Самоуверенность заставляет принимать необоснованные решения, которые зачастую приводят к неудовлетворительным результатам и разочарованиям. Давай возьмём, к примеру, профессиональную деятельность. В одном из исследований врачи, которые были полностью (то есть на 100%) уверены в своих диагнозах, ошибались в среднем в 40% случаев.

• Но я ещё студент!

• Хорошо. Студенты, которые оценили вероятность ошибки в 1%, ошиблись в 27% случаев. В другом исследовании студентов попросили оценить, в какие сроки они сдадут свои курсовые. Причём их попросили назвать три даты: к какому числу они сдадут с 50% вероятностью, с 75% И 99% вероятностью. В 50% сроки уложились только 13%, в 75% сроки уложились 19%, а в 99% сроки завершили только 45% студентов, то есть меньше половины.

• Может, они не были заинтересованы угадать? Может, надо было их дополнительно замотивировать? Деньгами, например.

• Учёные пробовали, сотня баксов не улучшила ситуацию. Они даже пробовали пугать испытуемых перспективой показаться глупыми перед сверстниками. Это не работает.

• Звучит грустно. Но мне то, что делать? Может, стоит уже смириться с тем, что я ничего не знаю? Есть же эффект Даннинга — Крюгера, который говорит, что люди, которые только начали, в чём-то разбираться, переоценивают свои убеждения. Значит, надо просто считать, что ты ни в чём не разбираешься, и всё.

• С эффектом Даннинга — Крюгера не всё так просто, но об этом в другой раз. В любом случае это не выход. Я называю позицию: “я знаю, что ничего не знаю” - грехом неуверенности. Проблема в том, что кое в чём ты всё-таки разбираешься. А в чём-то даже довольно неплохо. И свалить все эти убеждения в одну кучу - плохое решение. В твоей голове получится полный бардак. Ведь там, где у тебя вполне достаточно данных для приемлемого прогноза, ты заявишь, что недостаточно уверен. Вернёмся к тем же врачам. Представь, что ты пришёл узнать результаты анализов, а врач говорит: ну, наши тесты не обладают 100% точностью, поэтому я ни в чём не уверен._

• Но разве скромность — это плохо?

• Ложная скромность с занижением реальной оценки твоих знаний — это ужасное решение, из-за которого ты постоянно будешь упускать возможности.

• Самоуверенность — это плохо, неуверенность это плохо. Что же тогда хорошо?

• Правильная степень уверенности.

• Это как?

• Тебе нужно разложить убеждения по полочкам в соответствии с тем, насколько ты в них уверен.

• А зачем тут цифры?

• Это уровни уверенности. Я нанёс их для того, чтобы ты мог потренироваться в калибровке.

• В калибровке? Про которую ты говорил в начале?

• Да. Калибровкой обычно называют сравнение показаний измерительного прибора с эталоном. Но прежде чем провести сравнение результатов твоего мозга с эталоном, давай сначала соберём данные. Я задам тебе 40 вопросов, на которые тебе нужно будет ответить просто да или нет, а затем добавить степень твоей уверенности.

• А почему минимум 55%?

• Так как вариантов ответов всего два, то если ты совсем не знаешь, то ставь 55%, и бросай монетку. Я взял вопросы из книги Джулии Галеф.

• Понял.

(Некоторое время спустя…)

• Кажется, разложил.

• Отлично. Смотри, это полка 55%.

• То есть, грубо говоря, половина ответов, или убеждений здесь неверны. Вот только ты не знаешь, какие именно. Но если здесь и правда около половины правильных, значит, у тебя хорошая калибровка. Это — эталон. На 75% полке должны быть правильными три из четырёх ответов. А на самом верху должна быть всего одна ошибка на 20 ответов.

• Ааа, вот как это работает.

• Сравнение этого эталона с твоим результатом и называется калибровкой. Давай взглянем, что у тебя получилось?

• Зелёная линия -это идеальная калибровка. А красная линия — это твои ответы. Чем сильнее отклонение, тем хуже твоя калибровка. Напомню, что в данном случае неважно отклонение в сторону слишком сильной уверенности или слишком слабой. И то и другое одинаково плохо. В первом случае ты будешь делать необоснованные ставки и вкладываться в малоперспективные авантюры. Во втором же случае ты будешь переплачивать за страховку и упускать реально выгодные предложения.

• Кажется, моя калибровка не идеальна.

• Не переживай. Ты не одинок. Исследователи Альперт и Раиффа задали испытуемым 1000 вопросов по общеизвестным темам. Вопросы были из разряда «сколько таксистов работает в вашем городе?». То есть ответы были численными. Затем их попросили обозначить 98% доверительный интервал для всех ответов.

• 98% чего?

• Доверительный интервал, это когда ты говоришь что-то вроде: я уверен на 98% что таксистов больше чем 500, но меньше  чем 50 тысяч. То есть 98% доверительный интервал означает, что реальный ответ попадёт в твой диапазон 980 раз из 1000. Ну представь, что ты начинаешь стрелять и я спрашиваю, какого размера должна быть мишень, чтобы ты 98 раз из 100 попал. Понятно, что чем меньше я буду требовать попаданий, тем меньше будет мишень.

• Кажется, понятно.

• Ну а ошибиться здесь будет значить, выяснить, что в реальности таксистов меньше или больше установленных тобой порогов. Если их 200 или 200 тысяч.

• Теперь понятно.

• Вернёмся к испытуемым, которые обозначили свои 98%-интервалы для тысячи вопросов. Если бы их калибровка была идеальной, то мы должны были бы ожидать, что в среднем 980 ответов попадут в доверительный интервал, а 20 промахнутся.

• Судя по всему, промахов было больше

• Сильно больше. 426!

• Оу. А моя калибровка, не так уж и плоха. Но хотелось бы получше, конечно. А кто-нибудь вообще хорошо откалиброван?

• Да, но ты не поверишь.

• (Скептический взгляд)

• Найт Сильвер написал целую книгу, где исследовал то, насколько хороши в прогнозах различные прогнозисты. И есть одна служба…

• Не тяни уже, что это за служба?

• Это национальная служба погоды США.

• Прогнозы погоды? Но они же всегда врут?

• Насколько ты в этом уверен?

• На 95% (ставит это убеждение на верхнюю полку)

• Тогда взгляни на график их калибровки

• Но этого не может быть

• Конечно, далеко не только прогнозисты погоды обладают хорошей калибровкой. Но об этом, пожалуй, в другой раз. Раз уж ты так уверен, то я обязан тебя предупредить: поаккуратнее с верхними полками.

• Потому что с них что-то, может, упасть?

• Ну можно и так сказать. Исследователи выяснили, что, когда речь идёт о небольшой уверенности всё было довольно неплохо. У них в эксперименте люди делали ставки на правильность своих ответов. Пока ставки были 1к1, 2к1 и 3к1 (то есть с уверенностью 50%, 66,6% и 75%) всё было довольно неплохо. Проблемы начинались выше, потому что по мере поднятия ставок от 3к1 почти ничего не менялось. То есть точность возрастала сильно медленнее роста уверенности. При ставке 100к1 верными оказались 73% ответов, при 1000к1 верными оказались лишь 81%. То есть там, где следовало бы поставить примерно 4к1, люди ставили 1000к1. И что хуже всего, исследователи обнаружили склонность людей к экстремально высоким ставкам (то есть к огромной самоуверенности)!

• Вот блин. Придётся снять это (пробует снять убеждение с верхней полки). Чёрт, не снимается. Похоже, за что-то зацепилось.

• А, это твоё эго. Видишь ли, демонстрируя сильную уверенность, ты поставил свою репутацию. К тому же в дело вступили эмоции. А они в этой ситуации не очень надёжный помощник и уж точно не мерило достоверности. Если тебе очень нравится во что-то верить, это не должно влиять на твою ставку. Ведь в реальной жизни ты ставишь не только деньги и репутацию, но зачастую и здоровье. Если ты регулярно будешь игнорировать свидетельства, которые тебе не нравятся, то со временем у тебя начнёт дребезжать адекватность.

• Ладно, я понял (снимает, наконец, убеждение с верхней полки). И что я теперь должен для каждого своего убеждения придумать какую-то оценку и постоянно их менять?

• Нет. Цифры я рисовал для тренировки и демонстрации принципа. Конечно, в реальности постоянно назначать осмысленные вероятности — невыполнимая задача. Но при этом всё ещё практически полезно думать об убеждениях не качественно (когда у вас есть только два варианта: знаю / не знаю), а количественно. То есть держать в голове вот такие полки, и хотя бы приблизительно закидывать убеждения в какую-то их часть. Повторюсь, мы не счётные машинки, и оперировать цифрами для нас очень сложно, поэтому чаще всего делать этого не стоит. Но если очень нужно, то я расскажу один лайфхак под названием тест эквивалентной ставки. Давай возьмём для примера какое-нибудь предсказание. Допустим, ты пытаешься понять, насколько ты уверен в том, что в течение трёх лет в твоём городе появится такси без водителя. Чтобы «оцифровать» свою уверенность в этом убеждении, попробуй следующее. Представь, что тебе дают на выбор два варианта: 1) предсказать, что такси появится, и если так и будет, ты получишь миллион рублей, и 2) тебе дают вытянуть вслепую шарик из коробки, где один белый и три чёрных шарика, и если ты вынешь белый, то получишь миллион рублей. Что ты выберешь?

• Ну это легко, я бы взял шарик.

• Значит, твоя уверенность меньше 25%. Пусть шариков теперь будет один белый и 15 чёрных. За белый миллион. Или ставишь на беспилотное такси?

• Не, ну тогда всё-таки на такси. Шансы есть.

• Твоя убеждённость выше 6%. А если один белый и 8 чёрных?

• Хм. Я даже не знаю.

• Вот и нащупали. Около 11%. В принципе, ты можешь оцифровать любое убеждение с любой точностью. Хотя на практике это почти никогда не нужно.

• Ладно. Но я же не могу волшебным образом разложить все свои убеждения по полкам. Я уж молчу о том, чтобы разложить хорошо, тут бы хоть как-то раскидать.

• Да, порядок тут мгновенно не появится. Да и некоторая степень хаоса будет всегда присутствовать. Это тяжёлая работа, но ты можешь начать с малого. Разложи, то что используешь прямо сейчас. Ты вот принёс мне убеждение. Выбери для него полку. Со временем класть убеждения на свои полки, и периодически перекладывать, когда узнаёшь новые данные, войдёт в привычку. У тебя в голове появится внутренний секретарь, который в случае твоего громкого заявления начнёт постепенно шептать: убедитесь, что у вас достаточно фактов для такой уверенности. Со временем он окрепнет и начнёт орать. Наведение порядка в голове — это не героический спринт, а терпеливый марафон. Это не волшебная кремлёвская диета, а здоровое питание на всю жизнь.

• То есть для начала мне нужно просто иногда задумываться о том, насколько я уверен в том, что озвучиваю и какие для этого есть основания?

• Да. Со временем ты почувствуешь, что некоторые “основания” тебя часто подводят, а другие, наоборот, более надёжны. У тебя появится собственный протокол для руководства своим складом.

• Выглядит посильно.

• Вот и здорово. Тогда я пошёл.

• Стой, ты же обещал волшебный способ улучшения калибровки, или я неправильно понял.

• А, точно. Альперт и Раиффа, ну те, что просили установить доверительный интервал, провели повторный эксперимент. Они полностью повторили изначальные условия, но перед тем, как дать испытуемым приступить к работе, они показали результаты прошлого эксперимента и разъяснили концепцию калибровки. Затем испытуемые также установили 98% доверительный интервал, и на этот раз в среднем выпали уже 190 ответов (было 426), что, конечно, далеко от идеала, но сильно лучше прошлого раза. Так что я уже улучшил твою калибровку.

• (Себе под нос) подожди-ка, это значит, что Сашка, который мне так уверенно что-то заявляет…

• Ооо, блин. Стой. Я забыл. Знания о калибровке нужно применять к себе, а не использовать против того, с кем ты несогласен! Иначе ты можешь попасть в долину плохой рациональности!

• (Загадочно улыбаясь) А насколько ты уверен в этом?

Наш мозг по умолчанию воспринимает, что как я о мире думаю, таков он и есть. Это когнитивное искажение называется «наивный реализм» и я о нём уже рассказывал. Однако задумавшись, мы легко понимаем, что не все наши убеждения точно отражают реальность.

Вот например Ханс Рослинг в начале своей книги «Фактологичность», задает 12 вопросов на знание базовых фактов о мире. Я приведу три из них.

Вопрос 1: За последние 20 лет доля мирового населения, живущего в нищете…

• почти удвоилась

• осталась почти неизменной

• сократилась почти вдвое

Вопрос 2: Сегодня в мире насчитывается 2 миллиарда детей (до 15 лет). Сколько детей согласно прогнозу ООН будет в мире в 2100 году?

• 2 миллиарда

• 3 миллиарда

• 4 миллиарда

Вопрос 3: Сколько годовалых детей в мире прививается сегодня от каких либо болезней?

• 20%

• 50%

• 80%

Пройти полный тест вы можете по ссылке (или в книге «Фактологичность»). Так вот, Рослинг выяснил, что в среднем люди отвечают правильно лишь на 2 из 12 вопросов, что буквально хуже чем результат обезьян, которые угадывали бы случайно. Обезьян здесь Рослинг использует просто как образ случайности, генератор случайных чисел справился бы так же (и тот факт что люди справились хуже - выдаёт закономерность, но это тема отдельной статьи).

Наши знания о мире могут устаревать, быть неверными или искаженными в какую-то конкретную сторону. Довольно скверно, ведь на основе этих устаревших знаний принимаются крайне важные решения. На всемирном экономическом форуме в Давосе в 2015 году Рослинг задал те же три вопроса политикам и главам международных корпораций. На вопрос о бедности они ответили значительно лучше обывателей (они знали, что доля живущих в нищете сократилась почти вдвое), но на вопросы о росте населения (детей согласно прогнозу будет столько же) и распространенности вакцинации (80%) хуже, чем можно было бы ответить случайно, то есть хуже обезьян. Решения принимаются на основе информации, и сложно отрицать, что релевантная информация могла бы улучшить их качество.

Но к счастью вы не принимаете никаких решений на основе этих данных, ведь вы же не политики и не главы международных корпораций. Ну ошибётесь вы рассуждая за чаем о том, что бедность в мире растёт. Это же не влияет на вашу жизнь. Вам-то вполне достаточно тех знаний, что у вас есть, чтобы эффективно принимать решения. Ведь так? Да, кстати, а где вы их получили, и почему вы так уверены что их достаточно?

Может вам дали их в школе? Ну это вряд ли. Ведь школа даёт самый базовый уровень знаний. Школьные знания это очень упрощённый срез актуальной научной картины мира, адаптированный для несформированного, в хорошем смысле, детского мозга.

Но даже если бы школьная программа содержала достаточный уровень знаний для вашей жизни (что бы мы не подразумевали под этим термином), она не способна просто загрузиться к вам в мозг без потерь. Но даже то, что не потерялось на этапе передачи знаний, похоже не так уж надёжно хранится.

Не верите? Вот* опрос в котором вопросы из школьной программы задавали взрослым людям. Там было всего 7 вопросов. Как думаете, сколько человек справилось со всеми вопросами?

Не самый впечатляющий результат. Как так вышло? Наверняка людям с бухты барахты задали вопросы из школьной программы какого-нибудь 10 класса, что-нибудь о дигибридном скрещивании или попросили решить неравенство с логарифмом. Конечно они не справились.

Вот только в реальности это был тест, решать было ничего не нужно, только выбрать верно или ложно утверждение. Вот список этих утверждений:

• «Электрон меньше, чем атом» (верно)

• «Вся радиация создана человеком» (ложно)

• «Пол ребенка определяют гены отца» (верно)

• «Лазер работает, фокусируя звуковые волны» (ложно)

• «Антибиотики убивают не только бактерии, но и вирусы» (ложно)

• «Континенты, на которых мы живем, движутся уже миллионы лет и будут продолжать двигаться в будущем» (верно)

• «Обычные растения – картофель, помидоры и т.п. – не содержат генов, а генетически модифицированные растения — содержат» (ложно)

На всякий случай отмечу, что подобные опросы проводятся по всему миру, и результаты не очень отличаются. Так что даже если принять допущение, что школьная программа полностью загружается в наши навигаторы, судя по всему значительная её часть очищается для экономии места.

Это порождает забавные баги в работе нашего навигатора. В другом опросе почти половина Россиян не смогла назвать регионы (или хотя бы один из них) в которых находится озеро Байкал. При этом там хотели бы побывать 37% опрошенных. То есть некоторые люди буквально хотели бы оказаться там, сами не знают где.

Но с другой стороны может и не не нужны все эти лишние знания? Билет на Байкал можно купить и не зная регион. Вот, например, Шерлок Холмс, утверждал что не засоряет голову лишней информацией, вроде информации о том, что Земля вращается вокруг Солнца

Ватсон, поймите: человеческий мозг — это пустой чердак, куда можно набить все, что угодно. Дурак так и делает: тащит туда нужное и ненужное. И наконец наступает момент, когда самую необходимую вещь туда уже не запихнешь. Или она запрятана так далеко, что ее не достанешь. Я делаю по-другому. В моем чердаке только необходимые мне инструменты. Их много, но они в идеальном порядке и всегда под рукой. А лишнего хлама мне не нужно. — Учение Коперника, по-вашему, хлам?! — Хорошо. Допустим, Земля вращается вокруг Солнца. — То есть... то есть... КАК — допустим? — Земля вращается вокруг Солнца. Но мне в моем деле это не пригодится!

Шерлок Холмс, конечно, выдуманный персонаж, но подобная точка зрения не редкость и среди реальных людей. Мол я хороший специалист, зачем мне забивать голову ненужной ерундой.

Вы же хороший специалист? Правда согласно статистике каждый второй россиянин не работает по специальности (а может каждый третий, или всё таки две трети?). То есть многие из тех, кто получил в свой арсенал полезные инструменты для своей деятельности, зачастую не пользуются этими самыми инструментами.

Но даже если вы угадали со специальностью, даже если ваша учебная программа дала всё необходимое для вашей профессиональной деятельности, и даже если ваша специальность по какой-то странной причине не требует обновлять ваших знаний о ней, разве специальностью ограничиваются необходимые знания о мире?

Случайно ли, что автор произведений о Шерлоке Холмсе, Артур Конан Доил, увлекался спиритизмом и оккультными практиками? В любом случае, радикальный подход заужающий необходимые знания до профессии, рождает ситуации из разряда: возьму-ка я астрологический прогноз о том, стоит ли мне начинать бизнес. Сергей Абдульманов, в одной из статей рассказывал о том, как они запускали сервис экспертных консультаций для предпринимателей. Но оказалось, что люди не очень то хотят платить за консультации каких-нибудь юристов, зато с удовольствием кинулись платить за астрологов и тарологов. Не удивительно, ведь согласно опросу* только 24% из опрошенных россиян чётко ответили, что астрология не наука.

Но какая разница, ведь это знание не влияет на принятие важнейших решений в вашей жизни? Почему бы не сделать расклад таро на выбор спутника жизни? Не обратиться к альтернативной медицине за лечением? Не узнать у нумеролога ваше предназначение и подходящую профессию? Ведь всё это «не важные решения».

Но это не мотивационное эссе о том, что нужно знать всё на свете. Многие штуки могут быть вам не интересны (как например знание о том, что земля и солнце вращаются вокруг общего центра масс). Это как раз нормально, но речь не про интерес. «Узкий специалист» говорит о пользе. Он уверен, что знает, какая информация полезна, а какая бесполезна для его жизни. Он не готов тратить ни секунды драгоценного времени на поверхностные знания отклоняющиеся от выбранного курса. Вот только достаточно ли ему знаний для правильного выбора курса, и будет ли этот курс вечен? Радикальная борьба с расширением кругозора иногда приводит к страшному диагнозу «хронической информационной удовлетворенности» (пометка: это не реальный диагноз). Это когда «я знаю уже всё, что нужно». Так печально видеть людей, которым его поставили в молодом возрасте. Можно ли спастись от этого недуга?

Принимайте минимакс.

Это не лекарство, разве что в фигурально смысле. Это список вопросов по различным тематикам, который составлен по результатам опроса ученых, преподавателей и популяризаторов науки, который ставит целью сформировать связное представление о мире в голове современного человека.

Там нет ответов, только вопросы. И это, конечно, далеко от персонализированного списка вопросов важных лично для вашей жизни. Но цель этого списка в другом - сохранить ваше любопытство в живых. Ведь если оно умрёт, то упадут шансы ответить на самые важные вопросы, от которых прячется «узкий специалист» за показным прагматизмом.

На часть вопросов из списка минимакс помогут ответить плейлисты по темам, которые я заботливо отбирал на протяжении последних трёх лет. Там есть плейлисты о нашем мозге, математике, звёздах, происхождении жизни, эволюции и многом другом.

Конечно, задаваться вопросами из минимакса это не единственный способ бороться с «хронической информационной удовлетворенностью». Делитесь своими способами в комментариях.

И как сказал Ричард Фейнман: «Разумеется жизнь у каждого из нас только одна, и когда вы совершаете все положенные вам ошибки и начинаете понимать, чего вам делать не следует, тут-то она к концу и подходит». Не подсмотрел ли он это изречение у народной мудрости «век живи, век учись, помрешь дураком». Не знаю, но уверен, что к этой пословице он наверняка бы добавил: «ну хотя бы не таким, как если бы не учился».

О, и кстати. Данные по вопросам из начала статьи уже устарели, ведь книга Рослинга издана в 2017 году. Обновим?

*-выполняет функции иноагента.

• Где это я?

• Привет! Я - это ты из будущего, и я расскажу тебе, почему логические ошибки, в которые ты вечно тыкаешь другим, зачастую не являются ошибками, да и те, что являются - не всегда логические. А часть из них вообще противоречат друг другу.

• О, разговор с собой из будущего, какой избитый приём. Но ты меня заинтересовал. Ты утверждаешь, что некоторые логические ошибки — не ошибки? Приведи пример.

• Хорошо. Эталонная логическая ошибка — это апелляция к эмоциям. Соискатель приходит на собеседование и вместо ответа на вопрос о квалификации начинает перечислять, что дома его ждёт жена-инвалид, у него семеро детей и им нечего есть и нечего надеть.

• Ну, всё верно, соискатель ведь, правда, не прав, значит, это ошибка!

• Да, он не прав. Но это не имеет никакого отношения к апелляции к эмоциям. Не она делает его утверждение неверным.

• Ты имеешь в виду, что в данном случае проблема в отсутствии квалификации, а не в давлении на жалость?

• Именно, он не ответил на вопрос работодателя. Если бы он не давил на жалость, это ничего бы не поменяло. Более того, хорошая речь должна вызывать эмоции, просто чтобы её дослушали. Отец классической логики, Аристотель считал так называемый “Пафос”, то есть влияние на эмоции аудитории, важным элементом ораторского мастерства.

• Ага, вот ты и попался. Это же логическая ошибка, под названием «апелляция к авторитету». Так делать нельзя.

• Да ну. И почему же нельзя апеллировать к авторитету?

• Но это же всем известно? Ой, это же апелляция к большинству... Ну тогда, потому что… эм… потому что классическая логика — это очень авторитетный авторитет, который, гласит, что так делать нельзя?

• В точку.

• Блин, но это же ошибка под названием “порочный круг”. Нельзя же говорить “мы не верим авторитетам, потому что верим в авторитет логики”.

• Да. Обычно сразу после фразы “не доверяйте авторитетам”, следует рекомендация “пользуйтесь проверенными источниками информации”. Никто не видит в этом противоречия? На самом деле проблема в том, что мы не можем разбираться во всём. Мы не можем даже разбираться во всём, в чём хорошо было бы разбираться. Поэтому мнение эксперта вполне себе является аргументом, если у тебя нет возможности разобраться в вопросе самостоятельно. А ссылка на исследование с хорошим дизайном — это апелляция к авторитету научного метода, и это не плохо. Это, конечно, не значит, что выбор авторитета, которому стоит верить, это дело вкуса, но об этом в другой раз.

• Ну вот, на самом интересном месте.

• О, это не самое интересное. Что, если я скажу, что, пожалуй, самая известная логическая ошибка «ad hominem» или «переход на личности» не всегда ошибка?

• Че-е-его?

• Если твой собеседник по какой-то причине подбирает информацию однобоко, это может напрямую относиться к сути спора. Ты же наверняка слышал что-нибудь о термине «конфликт интересов».

• Это когда производитель бадов сам проверяет свои средства на безопасность и эффективность или вроде того?

• Да. В таких случаях считается хорошим тоном, если ты в обсуждении сразу заявляешь о том, что ты ангажирован, или иными словами заинтересован, в том, чтобы оказаться правым. Твои аргументы могут быть подобраны однобоко, причём даже не умышленно. И для меня как собеседника, это очень даже релевантная информация. А если мы выступаем перед аудиторией, то и для них тоже. Так что в каком-то смысле здесь ad hominem вполне уместен. Однако также хорошим тоном считается не затрагивать личность собеседника, даже если информация о его личности является непосредственно связанной с его заявлениями.

• Я что-то запутался. “Апелляция к личности” это всё-таки плохо?

• Это сомнительное с этической точки зрения решение, за которое в быту можно получить в глаз. Однако это не логическая ошибка. Как и родственное ему «отравление источника». Популяризаторы науки часто упоминают так называемые «мусорные научные журналы». Это такие издания, которые за деньги готовы опубликовать любую чушь под видом научной статьи. Так вот, если ты предоставишь публикацию из подобного журнала, то я заявлю, что, вероятнее всего, она не несёт научной ценности и это будет «отравлением источника». С другой стороны, если я предоставлю публикацию из «Nature», упомянув источник, ты заклеймишь меня за «апелляцию к авторитету».

• Оу, но это не должно так работать.

• Но именно так и выглядит бездумное применение знаний, полученных из ролика «10 главных логических ошибок за 5 минут». Подобный список - это вовсе не строгая система, построенная на логике. Значительная часть «логических ошибок» это набор противоречащих сами себе костылей, которые иногда работают как надо.

• Противоречащих сами себе?

• Конечно. Взгляни на ошибку под названием «сам такой» (иногда это называют «вотэбаутизм», или апелляция к лицемерию).

• Это как если бы я указал тебе на логическую ошибку, а ты, вместо того, чтобы её исправить сказал бы, что я сам допустил её раньше в обсуждении. Получается ты не прав, ведь я раньше указал тебе на ошибку!

• Я смело могу заявить о том, что ты совершаешь ошибку под названием «двойные стандарты», ведь указываешь мне на правила, которые сам не соблюдаешь. Но далеко мы так не уйдём. Обрати внимание, обе эти ошибки направлены на то, чтобы выяснить, кто из собеседников неправ.

• Так в этом же и есть суть спора?

• Нет, суть спора в том, чтобы выявить правильную позицию.

• Но в чём разница?

• Ну в одном случае ты пускаешь всю свою интеллектуальную мощь на то, чтобы показать, что твой оппонент - демагог и софист, а его речь наполнена манипуляциями и полемическими уловками. Он, кстати, занимается тем же самым. В таком случае знание о логических ошибках выступает как оружие. Оно и было разработано для этого, ведь, по сути корнями уходит в инструментарий публичных дебатов.

• Ну, допустим это выглядит не очень привлекательно. Но что ты предлагаешь? Выкинуть мои знания о логических ошибках на помойку?

• О, это обычно называют ложной дилеммой (или ложной дихотомией). Когда ты говоришь «я должен либо тыкать всем без разбору в логические ошибки, либо не использовать знание о них». Раз уж мы затронули ложную дилемму, то я обращу внимание, что она также не связана с логикой. Это скорее эвристика, лайфхак, который полезно использовать для проверки, достаточно ли вариантов мы рассматриваем. Два варианта может быть мало, но и добавление третьего ещё не означает, что теперь их достаточно. Поэтому возможна ложная трилемма, или четырелемма. Чип и Дэн Хиз в книге «Ловушки мышления» называют такое неосознанное заужение своего выбора - «узкой рамкой». Но как ни назови, это не ЛОГИЧЕСКАЯ ошибка, хоть и полезно этого избегать.

• Ты ушёл от ответа, но, к счастью, я всё записываю. Какой вариант применения логических ошибок я упускаю, и почему не стоит тыкать в них у оппонента?

• Забавно, что твой вопрос является частично и ответом. Смотри, я указал тебе на то, что ты применяешь ложную дилемму. То есть я указал тебе на ошибку, пусть бы она была и логической. Но у тебя не возникло ощущения, что ты получил ответ, потому что ты его и не получил.

• Да, я его до сих пор не получил.

• Это часто происходит в дебатах, где главная цель - это выявить ошибки собеседника и доказать свою правоту. Ведь нам кажется, что если собеседник ошибся, то он потерял баллы, а стало быть, мы заработали. Однако это не так, и ошибка оппонента на самом деле не влияет на реальное обстоятельство дел, которое (в идеале) мы пытаемся выяснить.

• Как это не влияет? Если собеседник ошибся, значит я прав?

• О, кажется, тут что-то пропущено. Давай восстановим логическую цепочку. Если собеседник ошибся, значит его позиция не может быть правдой, а ложность его позиции однозначно доказывает правдивость моей, значит я прав. Такие штуки любят называть «скрытыми допущениями», и каждое допущение требует отдельного доказательства.

• Оу, не всё так просто, да?

• Именно. Человек может быть прав, но при этом допускать логические ошибки. Вспомни школу. Если твоё решение математической задачки неверно, ты всё ещё можешь случайно прийти к правильному ответу.

• Но шансы таким образом решить задачку правильно не очень высокие!

• Это если ты не посмотрел в решебник. До большинства мыслей, которые мы озвучиваем, мы не дошли сами в результате дедуктивных умозаключений. Зачастую люди терпят крах при попытке обосновать, в общем-то верные суждения формальным образом, особенно если эти умозаключения были получены от кого-то. То есть они буквально берут верный ответ и обосновывают его неверными аргументами.

• Но мы ведь можем указать, что такое РЕШЕНИЕ неверно.

• Да, но не указать, что неверен ОТВЕТ. Ты спрашивал про суть спора. Так вот, если тебя действительно интересует ОТВЕТ, то вместо того, чтобы, покряхтывая от самодовольства, поздравить самого себя с блестящей победой, после того, как ты перечислил все «логические ошибки» собеседника указав на его неверное решение, всё же попробуй найти ответ. В идеале можно пропустить первый пункт, как не несущий пользы. Я называю это — установка на поиск истины.

• Ты имеешь ввиду, что можно не озвучивать логические ошибки оппонента, а сразу указывать на верное решение? Ну то есть в случае ложной дилеммы не тыкать в ошибку, а сразу озвучить недостающий вариант? Но нужны ли тогда вообще знания о штуках, которые мы называем логическими ошибками?

• О, конечно. Правда, для поиска истины подходят не далеко не все из этих штук. К счастью, есть простой способ их различать.

• А ты не мог с этого начать?

• Нет, так было бы неинтересно. Самое полезное применение для знаний о логических ошибках — это поиск и выявление их в своём собственном рассуждении. Но ошибки, которые призваны ткнуть в неправоту собеседника, очень плохо с этим справляются. В каких рассуждениях ты можешь себя поймать на ошибке «сам такой» или «апелляция к жалости»? Больше того, значительная часть самых полезных штук из списка «логических ошибок» - это штуки, связанные с теорией вероятности и статистикой, а не с логикой.

• Это какие, например?

• Ну вот, в статье про совпадения я рассказывал об «ошибке игрока», «ошибке выжившего», и ошибке под названием «корреляция не взаимосвязь». А в статье про рационализацию я рассказывал про мотивированный подбор аргументов, который в науке называют «cherry picking». Все эти штуки традиционно включают в список логических ошибок, хотя точнее было бы назвать их стастистическими или вероятностными. Чтобы лучше продемонстрировать принципиальную разницу приведу пример. В статье про доказательства я рассказывал о «поспешном обобщение».

Это когда мы делаем наблюдения: Вода кипит дома при 100 С°Вода кипит на улице при 100 С°Вода в лаборатории кипит при 100 С°А затем делаем вывод: вода везде кипит при 100 С° (что неверно, к примеру, в горах вода закипит при меньшей температуре).

• Эту ошибку ещё называют неполной индукцией. Подразумевая, что бывает полная индукция. Но на практике (в отличие от мира чистой математики) мы никогда не обладаем полной информацией, и нам всё равно нужно делать выводы. И это не страшно, просто выводы эти будут вероятностными. Однако в классической логике рассматриваются только варианты: утверждение верно или утверждение неверно. И без полной информации мы не можем получить никакого промежуточного результата. Это же, кстати, порождает костыли, вроде «ошибки анекдотического свидетельства».

• Это когда я утверждаю, что ты привёл лишь один пример или случай из жизни, и он не может опровергнуть моё утверждение?

• Да, но, по сути, ты просто пытаешься проигнорировать неудобное свидетельство. Если я тебе соврал, то проблема в том, что я соврал. Но если я не вру, то нельзя просто так взять, выкинуть свидетельство. В медицине, к примеру, подобные «анекдотические свидетельства» называются клинический случай, в бизнесе «кейс». Да, их реальность нужно проверять, но никто их не игнорирует. Потому что игнорировать свидетельства, ужасная идея. Для этой идеи, конечно же, тоже придумали соответствующую ошибку, под названием «ни один истинный шотландец».

• А это я знаю.

Ни один истинный шотландец не добавит сахар в овсянку.Но мой дядя шотландец, и он обожает овсянку с сахаром!Я же сказал «ни один ИСТИНЫЙ шотландец!».

• Да, в статистике подобные штуки относятся к махинациям с выборкой. Но о плохой статистике мы поговорим в другой раз.

• Ну, хорошо. Но если эти ошибки не связаны с логикой, то почему они называются логическими?

• Так сложилось исторически. Раньше логикой называли науку о правильном мышлении, а в корзину с логическими ошибками складывали все нарушения правильного мышления. Эта традиция продолжается и сейчас, теперь туда зачастую кидают даже когнитивные искажения.

• Но неужели ни одна логическая ошибка не является чисто логической?

• О нет, конечно, есть чисто логические ошибки. Их ещё называют формальными, потому что сегодня современная логика — это наука о формальных системах. Знание о них довольно полезно для любого человека, но к тому же жизненно необходимо для людей, работающих с формальными системами, например, для математиков, программистов или юристов.

• Вот это круто, и какие ошибки являются формальными?

• Всё, что нарушают таблицы истинности

• Че-е-его?

• О, я рассказывал о них в статье про логику, думал ты читал. Всё время забываю, что ты из прошлого. Там я рассказывал, то есть ты будешь рассказывать, про то, что называется формальными ошибками. Вот пример: если идёт дождь, то на улице будет мокро. И на улице мокро. Из этих посылок нельзя сделать вывод, что идёт дождь, потому что улица может быть мокрой и по другим причинам. Название такой формальной ошибки «подтверждения консеквента».

• Звучит невесело

• Да, у большинства ошибок довольно замудренные названия. Так вот, таблицы истинности наглядно показывают, какие логические заключения можно делать, а какие нельзя. К примеру, если у тебя есть утверждения: если идёт дождь, то на улице точно мокро, и наблюдение - на улице сухо, то вот из этих посылок можно сделать вывод, что дождь не идёт. У правильных выводов тоже есть свои названия, например, этот называется modus tollens.

• Это интересно, почему об этом не рассказывали в дебатном клубе, когда мы изучали логические ошибки?

• Потому что знания о логических ошибках и знания о логике, как ты видишь, пересекаются не так уж сильно. А поверхностные знания о логических ошибках приводят, фигурально выражаясь, к забиванию гвоздей микроскопом.

• Интересно. Но у меня остался ещё один вопрос, а разве наш с тобой диалог — это не парадокс, наподобие Апории Зенона?

• О, я бы мог рассказать суть апории Зенона в которой говорится, что «В гонке Ахилес никогда не сможет обогнать черепаху, если у неё будет фора в полпути, поскольку Ахилес должен сначала достичь точки, откуда стартовала Черепаха, но Черепаха уже пройдёт сколько-то за это время, и ему снова придётся догонять и так до бесконечности», но раз ты в курсе, то не стану её рассказывать. Но при чём тут она?

• Я имею в виду, раз я беседую с собой из будущего, то обновление информации в моей голове, разве не должно менять тебя, то есть меня, в будущем и твои действия? Короче, разве это не парадокс?

• А, ты про это? Не переживай. Мы просто персонажи, написанные для этого диалога. Наша цель лишь в том, чтобы рассказать о вреде бездумного применения знаний о логических ошибках и о пользе их корретного применения. Так что никакого парадокса нет. Как и нас.

Ночью в Берлинской обсерватории была открыта новая планета солнечной системы. Открытие осуществили Иоганн Галле и его аспирант Генрих Д’Арре на основе расчётов французского астронома Урбена Леверье. Наблюдение произведено экваториальным ахроматическим рефрактором фирмы Merz und Mahler. Это стало возможным благодаря тесному международному сотрудничеству в области астрономии, а также в результате значительного усовершенствования технических средств наблюдения за небесными телами.

Галле, открывший планету, предложил назвать планету «Янус». Леверье, сделавший вычисления хотел, чтобы планета была названа в его честь.

Примечательно, что астрономам впервые удалось найти планету благодаря предварительным вычислениям, а не с помощью методов наблюдения, как это было раньше.

В утреннем комментарии член Королевского Астрономического общества и Парижской академии наук Джордж Эйри отметил:

«Во всей истории астрономии и, даже я могу сказать, во всей истории науки не происходило ничего подобного… Уран, Церера, Паллада были открыты в ходе наблюдений, которые вовсе не предусматривали открытие планет… Но движение Урана, изученное учёными… указывало на действие некоторого возмущающего тела. Математики, наконец, решились приступить к работе, чтобы удостовериться в возможном существовании такого тела. Они показали, что предположение о возмущающем теле, движущемся по некоторой определённой орбите, полностью объясняет возмущение Урана. С твёрдостью, которую я должен характеризовать как замечательную, они выразили своё убеждение, что возмущающая планета должна находиться точно в некотором месте и иметь такой-то вид. Она действительно была найдена на этом месте и имела предсказанный вид. История астрономии не знает других подобных примеров

».

К сожалению, открытию точно не удастся избежать споров о приоритете. Выяснилось, что на данный момент уже имеются другие независимо сделанные вычисления.

Так, математик Джон Адамс из Кембриджской обсерватории получил схожие с Леверье результаты. Адамс, как и Леверье основывался на работах Алексиса Бувара. Напомню, что Бувар ранее обнаружил отклонение траектории Урана от прогнозируемой, указывающее на наличие неизвестного небесного тела.

Однако, в результате медлительной коммуникации с вышеупомянутым Джорджем Эйри из Королевской обсерватории в Гринвиче и директором Кембриджской обсерватории Джеймосом Чаллисом, вычисления Адамса не привели к активным наблюдениям. К сожалению, как заметил в одной из своих статей Астроном Владимир Сурдин, «хороших телескопов всегда меньше, чем хороших астрономов». У телескопа имени Джеймса Уэбба время расписано буквально поминутно.

Непонятным остаётся, почему у двух научных групп столько времени заняло решение проблемы, которая является элементарной для современных компьютеров. Видимо, какие-то причины тому были.

К сожалению, Иоганн Галле и большинство других исследователей, участвовавших в проекте, на текущий момент недоступны для комментариев.

Полагаю те из вас, кто интересуются не только новостями науки, но и её историей уже смекнули, что всё сказанное мной, правда, и все действующие лица реальны. Важная опущенная деталь, это то, что события этой «новости» происходили в 19 веке. Это история обнаружения планеты Нептун. И в отличие от множества научных сенсаций в современных СМИ она подтвердилась. Что ж, по-моему, эта первоапрельская шутка - отличный повод поговорить об увлечении научными сенсациями.

Не буду скрывать своего мнения, я считаю погоню за сенсациями пагубной привычкой. В статье про доказательства (здесь же на Пикабу) я уже говорил, что главная проблема историй (коими и являются научные сенсации) в том, что мы любим необычные истории.

То есть сложность именно в искажённом восприятии. Мы ожидаем, что научные сенсации верны, ведь они же научные. Но в реальности они в большинстве случаев неверны, ведь они же сенсации.

Откуда мы берём сенсации?

Процесс производства научного знания сопряжён с выдвижением огромного количества гипотез, из которых лишь единицы в итоге оказываются годными. СМИ же подсвечивают гипотезы на любом этапе, выбирая, конечно, самые странные и безумные.

Давайте покажу это на примере процесса разработки новых лекарств. Любое нормальное лекарство проходит ряд этапов проверок.

Сначала идёт ряд доклинических этапов: в пробирке, на клеточных культурах, на животных. По данным Национальных институтов здравоохранения, от 80 до 90% исследовательских проектов терпят неудачу ещё до того, как они проходят испытания на людях. При этом на каждый маленький шажочек здесь СМИ пишут заголовки вроде: «Учёные изобрели новое лекарство от рака». Биохакеры, в ответ на каждое мало-мальски удачное исследование на мышах, покупают новый БАД в свой суперарсенал.

И мы с вами поговорили ещё только про доклинику. Потом идут несколько фаз клинических испытаний на людях. Там так же отсеивается значительное количество «кандидатов». Вот в этой статье говорится о том, что лишь один из 1000 препаратов прорывается сквозь все исследования и доказывает свою эффективность.

Шансы на успех новой гипотезы или лекарства называются априорной вероятностью. На этапе выдвижения гипотезы они довольно скромные, ведь большинство гипотез отсеиваются на самом первом этапе. С каждым этапом отсева шансы увеличиваются, но на каждом этапе это лишь шансы на успех.

Здесь есть важная оговорка. Препарат не становится эффективным, как и научная гипотеза не становится верной. Они изначально являются таковыми, только вот мы этого не знаем. Неопределённость существует у нас в голове. С каждым этапом проверок мы обновляем свою уверенность. Тут был такой шанс, здесь уже другой. Вот этими самыми шансами, зачастую и пренебрегают в СМИ.

Пара примеров

Давайте вспомним недавнее прошлое. В 2011 году в эксперименте OPERA учёные зарегистрировали нейтрино движущиеся быстрее скорости света. Что вообще-то запрещает специальная теория относительности Эйнштейна. Сразу же полетели новостные заголовки: «Теория относительности опровергнута! Эйнштейн был неправ». И это могло бы оказаться так, наука не догматична. Как сказал Терри Пратчетт: «в науке самые важные места занимают те, кто смог опровергнуть постулаты чьих то убеждений, особенно основополагающих». Но из-за того, что СМИ не публикуют тысячи экспериментов, где СТО была подтверждена, акцент на одном эксперименте, где она была опровергнута, создаёт смещённое восприятие о шансах на тот факт, что это правда. Чем же закончилась эта история? Выяснилось, что на сложном оборудовании был неправильно подключен кабель.

Другой случай, чуть поновее. Обнаружение фосфина в атмосфере Венеры в 2020 году. Даже уважаемые мною спикеры не удержались от спекуляций на эту тему. Конечно же, посыпались заголовки: «Жизнь на Венере, Венера обитаема?» Оказалось, что за фосфин приняли другое вещество — диоксид серы. Доказала это другая группа учёных в рецензируемом журнале Nature Astronomy 28 июня 2021 года.

Трезвая оценка

Ещё раз подчеркну: дело не в том, что сенсации не могут быть правдой. Вопрос в нашем с вами восприятии и ставках на правдоподобие новостей. СМИ в результате оптимизации (осознанно или не осознанно) предлагают игнорировать знание о количестве «пустых» сенсаций среди всех новостей (что и является априорной информацией). Таким образом, они как бы призывают нас к диалогу. Эй ты, да-да ты. Смотри: этот эксперимент опровергает текущий научный консенсус. А ну-ка оцени, кто здесь прав? Кто, если не ты со своим другом на кухне, сможет понять ошибается ли научный консенсус?

Но как сказал Александр Панчин в одном из наших чаепитий:

«… место для информированной дискуссии по научным вопросам - это рецензированные научные журналы среди специалистов… Да иногда и научный консенсус может ошибаться, но если он и ошибается, то не вы это выясните. Загуглив пару сайтов в интернете вы не обретёте достаточной компетенции, чтобы опровергнуть научный консенсус, даже если он не прав»

Аккуратность научного сообщества

Об опасности игнорирования априорных шансов хорошо осведомлён Нобелевский комитет. Вообще-то Альфред Нобель завещал выдавать награду за открытия, совершённые в прошлом году. Чего нобелевский комитет не делает и почему-то выдаёт премию за открытия 10-20 летней давности. Такое решение обусловлено нежеланием краснеть потом за то, что премии были вручены за ошибочные открытия. Краснеть просто уже приходилось, вот пара примеров:

Йоханнес Фибигер в 1926 году получил Нобелевскую премию по медицине за открытие паразитического червя, вызывающего рак. Фибигер был первоклассным учёным и внёс огромный вклад в науку, в том числе в ранее развитие онкологии. Но в этот раз он ошибся, и премию получил поспешно.

Подобная история произошла и с Энрико Ферми. Один из величайших физиков 20 века получил Нобелевскую премию в 1938 году «за демонстрацию существования новых радиоактивных элементов, получаемых при облучении нейтронами, и за связанное с этим открытие ядерных реакций, вызываемых медленными нейтронами». Вот только новых элементов Ферми не открыл. Позже выяснилось, что он наблюдал ядерное деление, при котором ядра урана распадались на более лёгкие уже известные элементы.

Вообще-то, чем более сенсационным является заявление, тем больше времени и сил на самом деле потребуется для того, чтобы его обосновать и вписать в учебник. И тем меньше шансы, на то, что оно подтвердится. Даже эксперты в области не способны перепрыгнуть от априорной вероятности сразу к оценке шансов конкретной гипотезы.

Вот иллюстративный пример: есть такая ABC-гипотеза в математике, одна из проблем тысячелетия, между прочим. В 2012 году японский математик Синъити Мотидзуки заявил, что смог её доказать. И нет, я не ошибся - не доказал, а заявил, что доказал. Дело в том, что разработанный им для доказательства математический язык — дико сложная штука (это вам не английский за 3 месяца выучить). В мире есть десяток математиков, способных проверить доказательство, но у них внезапно свои дела. Ведь они специалисты экстракласса и работают над своими задачами. На сегодняшний день статус доказательства всё ещё неопределённый. И это вам не физика, где для некоторых доказательств нужно построить коллайдер за пару миллиардов долларов или космический телескоп за десять миллиардов. Это математика, работающая в мире чистых формальных моделей.

Что же я в итоге предлагаю?

Ну, во-первых, я не предлагаю отказаться от просмотра новостей науки в пользу истории науки или чего-то в этом роде. Я скорее призываю к трезвой оценке сенсационных заявлений, связанных с научными открытиями. Взгляните, например, на канал QWERTY, они постоянно отпускают ироничные шутки на тему наиболее неординарных заявлений учёных. Я считаю это вполне здравым подходом.

Ну и, конечно, я призываю восхищаться невероятными открытиями прошлого, которые сегодня уже попали в учебники. Да, какая-то часть из них окажется неверной, и кто-то даже получит за это Нобелевскую премию через 20 лет. Но процент моделей, которые окажутся неточны, там сильно отличается от выборки из газетных сенсаций. Закончу я, пожалуй, символичной цитатой Льва Ландау: «Произведение оптимизма на знания — величина постоянная».

Благодарности:

• За ссылки в "медицинский блок" Алексею Водовозову

• За примеры сенсационных новостей Валерию Иванову

О пренебрежении априорной информацией в бизнесе я говорил в этой статье.

Александр в ролике рассказал о так называемом "эффекте обратного действия". Это когда люди, получая достоверные аргументы, противоречащие их убеждениям, не меняют мнение, а укрепляются в правоте. Я об этом эффекте тоже рассказывал на Пикабу. (см. конец абзаца про Логику).

Эффект впервые обнаружен исследователями Найханом и Райфлером. И в СМИ он сразу приобрёл статус аргумента против популяризации науки и развенчания всяких-разных мифов. И это было бы хорошим аргументом, если бы эффект существовал. Однако независимые исследователи Портер и Вуд не смогли воспроизвести эффект несколькими годами позднее. Вот только на этом история не заканчивается, а начинается самое интересное.

Небольшое отступление. Давайте взглянем на комментарий, собравший под видео Александра больше двух сотен лайков: "Эффект обратного действия доказан. Учёные несмотря на опровержение фактами и не воспроизводимость эксперимента уверенно продолжают настаивать, что этот эффект есть. То есть даже экспериментальные данные разных исследований не смогли переубедить группу учёных, которые этот эффект придумали. Значит, эффект реально работает как минимум на учёных придумавших этот эффект".

К сожалению, я не закончил эту историю в вышеупомянутом ролике, хотя обмолвился о её продолжении (Александр также не развернул её до конца). Исправляюсь! Портер и Вуд ставили задачей своего исследования вовсе не проверку "эффекта обратного действия". Они планировали сделать академическую репутацию на работе о том, какие политические вопросы вызывают самый сильный "эффект обратного действия". Для этого они собрали гораздо бОльшую выборку, чем в оригинальном исследовании Найхана и Райфлера и взяли целых 36 тем. Каково же было их разочарование, когда хоть какой-то эффект обнаружился только в одном из 36 вопросов. Тогда они расширили выборку до 10 тысяч людей и 52 тем. Результат остался прежним...

Портер позже признался, что они были искренне уверены, что сделали что-то не так. Что они "поломали эксперимент". Найхан и Райфлер обладали внушительной академической репутацией, и Портеру было непросто сообщить "первооткрывателям" о том, что эксперимент не воспроизвёлся. Но он всё же сделал это. И, как вы уже догадались по приведённому комментарию, обе группы учёных с противоположными выводами продолжили отстаивать свои результаты а мы с вами так и не получили внятного ответа...

Если вы действительно подумали так, то не угадали. Вообще-то, Найхан тогда сказал: «Было бы ужасной иронией, если бы доказательства, противоречащие эффекту обратного действия, спровоцировали меня на удвоение этого эффекта». То есть, Найхан согласен с комментатором под роликом Александра - было бы и правда смешно. Но вместо этого все четыре исследователя объединили свои усилия и провели два новых исследования с ещё большими выборками. В результате все они подписались под следующим выводом: «Как и в случае с другими недавними исследованиями, мы находим мало свидетельств эффекта обратного действия на фактические убеждения респондентов».

Мне кажется, нам всем есть чему поучиться у Найхана и Райфлера.

«Многие критики, особенно наиболее ярые и философски подкованные, склонны, читая мою книгу, ограничиваться ее названием» Ричард Докинз

Вы путешественник, встречающий посреди поля забор. Если вы не знаете для каких целей этот забор установлен, худшее решение - это снести его. Причём это решение плохо именно потому, что вы не знаете функционального предназначения забора. Возможно он охраняет вас от чего-то очень опасного. Возможно он используется не так, как вы предполагаете. Так или иначе — ваше незнание о задачах, которые выполняет данная ограда вовсе не является поводом сносить её.

Этот факт подметил английский писатель Гилберт Честертон цитатой: «Никогда не ломайте забор, не узнав, зачем его поставили». Он таким образом хотел предостеречь от необдуманных реформ. Но как данный принцип может быть применён вне политики, в повседневности?

Не спешите сносить

Наши убеждения чем то похожи на заборы, о которых писал Честертон. Когда мы сталкиваемся с новым убеждением, которое кажется нам нелепым, у нас встаёт тот же выбор. Мы можем немедленно начать демонтаж. То есть промаркировать данное убеждением как глупое, а всех его носителей как людей недалёкого ума.

Но принцип «Забор/ограда Честертона» предлагает нам разобраться с какой целью и на каких основаниях существует убеждение, прежде чем бороться с ним.

Для этого нам понадобится пятьдесят грамм любознательности и тонну непредвзятости (зачем столько непредвзятости опишу в будущей статье про стилменинг и идеологический тест Тьюринга). Возможно мы выясним, что желание сносить забор было обосновано только нашим незнанием. Тогда мы сможем отказаться от необдуманных поступков.

Если же свидетельства покажут, что снос забора вполне обоснован, работа всё равно была проделана не зря. Теперь столкнувшись с защитниками забора (носителями убеждения), нам есть что обсудить. Диалог больше не нужно начинать с оскорблений и попыток ткнуть собеседнику пальцем в глаз. Мы можем обменяться с ним свидетельствами, а это в разы продуктивнее!

Конечно мы можем не договориться, особенно если хотя бы один участник дискуссии не разделяет ценность точных убеждений. Но это явно выглядит перспективнее, чем начинать разговор с сомнений в адекватности собеседника. А если нам повезёт, и собеседник будет настроен так же, мы можем прийти к наиболее оптимальному решению (не с точки зрения удовлетворить пожелания всех сторон, а с точки зрения получения лучшей модели).

Не спешите сносить ≠ не сносить вообще

«Естественный ход развития космических наук приводит к тому, что накапливаются новые данные, и во всеоружии новых фактов мы разгоняем войско устаревших идей» Карл Саган

Для демонстрации давайте обсудим изобретение «новой физики». Ну вы знаете, человек решает, что все физики ошибаются, а он изобрёл что-то принципиально новое. Чушь? Если знания человека в предметной области ограничены школьным курсом, скорее всего так и есть.

Но если он вник во все тонкости современной ему физики, возможно так и есть. Вся современная наука построена на людях, которые сдвигают границы нашего понимания. Кто-то действительно строит «новую физику». Разница лишь в том, что дилетант не может быть уверен в ложности того, чего не понимает. У него нет права сносить забор.

Таким образом, заниматься сносом конечно нужно. Ведь любое улучшение, это снесённый забор. Однако не каждый снесённый забор - это улучшение. Для развития города нужно регулярно демонтировать ненужные заборы (или хотя бы модернизировать). Но для этого просто необходимо отличать нужные от ненужных, иначе можно снести весь город (или не сносить вообще ничего от страха перед изменениями). Так что ограда Честертона - это не гимн против реформ и революций. Это призыв понять, с чем мы имеем дело, прежде чем начать действовать.

Равнодушие неопределённости

Все вышесказанное относится к случаю, когда забор вам действительно мешает. Демонтаж забора (борьба с убеждениями) дело затратное, оно стоит вполне ощутимых ресурсов. Поэтому важно помнить про вариант «пройти мимо». Нет, серьёзно, если убеждение показалось вам глупым, возможно так оно и есть. Человечество накопило несчётное количество заблуждений. Благодаря ускорению обмена информацией мы получаем доступ к тоннам чуши ежедневно. И я вовсе не призываю вникать во всё это. Если забор можно спокойно обойти, то стоит ли вообще с ним связываться? Но маркировка его каким либо определённым образом - это действие. Либо честно идите мимо, либо вникайте - здесь нет царского пути. В ином случае неизбежно вырабатывается не самая продуктивная привычка маркировать чушью любое непонятное убеждение.

Важные оговорки

• Этот принцип относится только к новым, непонятным идеям. Поэтому он не может использоваться для защиты. Ведь нам уже должны быть известны все обоснования того, в чём мы уверены. Так что стоит воздержаться от использования ограды Честертона в качестве универсальной защиты своих необоснованных убеждений.

• Если забор нужен и работает, но можно сделать лучше - нужно делать. Уродливые заборы не украшают город, а точные убеждения должны без сожалений заменяться ещё более точными.

• На оценку ценности забора никак не должны влиять потраченные на него ресурсы. Если это старый забор, который стоил кучу денег и он бесполезен, его нужно сносить. Если мы потратили кучу времени на то, чтобы изучить какую-нибудь нерабочую модель, это не должно становиться аргументом за полезность данной модели (впрочем эту идею я планирую развить в статье про невозвратные потери).