Когда пишут 1+1=3 это понятно, имеется в виду, что 2 покупаешь, а третий бесплатно, а тут что имеется в виду?

Взял отсюда. Снято вот тут

Пикабушники, среди вас есть физики-математики? Предыстория (отсюда можно пропускать, ctrl-F: запускать), арендовал значит небольшой домик в деревне Глинково под Сергиев Посадом на месяц на лето под удаленку (уже третий год один и тот же дом снимаю на месяц), сижу неделю кайфую, звонят родственники (живут в Мытищах), просят на неделю-две пристроить к себе племянника, типа школа закончилась, им надо поехать отдохнуть, а его деть некуда. Аргументы типа я как бы на работе не канают, тк как мы работаем на удаленке всем известно. И попросили, чтобы он балду совсем не гонял куда нибудь пристроить хоть на пару часов в день. Ну я душа добрая (или не очень как можно понять дальше) ну ок-везите. Он уже довольно взрослый, особо прям контролировать не надо, деревня фигли (хоть и модная, отстроилась мое почтение). Пока собирались-везли, думал куда пристроить, так вот: в прошлом году шел из магазина, вижу дед лет 80(85 как оказалось) несет сумки, еле тянет, ну я решил помочь донести до квартиры в соседней пятиэтажке, пока шли разговорились и выяснилось: дед когда-то работал в каком то советском НИИ ХЗМНОГАБУКОФФ, после распада переехал сюда, живет на пенсию и репетиторствует по математике и физике. Зашел к нему, квартира как квартира, интернета нет, живет как наполовину отшельник, себе на уме, есть старый телек, куча книг и дофига досок для записей и на них судя по всему попытки вызвать Дьявола или Лилит ну как минимум. Кароче, куда пристроить нашел, но суть вообще не в этом. Я как-то решил к нему зайти забрать мелкого и тут вспомнил про нерешенные задачи тысячелетия (https://ru.m.wikipedia.org/wiki/Задачи_тысячелетия), решил думаю дай угарну над мужиком, распечатал пару из них прям из Википедии и под видом помочь брату студенту на сессии попросил доказать (типа дали задания похожие на те, что будут на экзамене), ну и отдал ему, а не глянете (ну и усложнил, мол, ответ должен быть кратким и емким), он молча типа ок и взял (как выяснилось он почему-то и понятия не имел, что такие «загадки» есть). Кароче я распечатал “задания”: ( запускать) 1) Докажи, что для любой простой компактной калибровочной группы G квантовая теория Янга — Миллса для пространства R^4 (четырёхмерного пространства-времени) существует и имеет ненулевую спектральную щель. (Это Теория Янга — Миллса); 2) Докажи, что все нетривиальные (то есть имеющие ненулевую мнимую часть) нули дзета-функции Римана имеют действительную часть 1/2 (гипотеза Римана); 3) Докажи математически, что если положительный ответ на какой-то вопрос можно быстро (за полиномиальное время) проверить (используя некоторую вспомогательную информацию, называемую сертификатом), то верно ли, что и сам ответ (вместе с сертификатом) на этот вопрос можно быстро найти? (Равенство классов P и NP).

Кароче, опущу детали, получил следующие ответы (там по сути со слов записывал, нибуя не понял, могу ошибиться): 1) В квантовой теории Янга — Миллса в четырех измерениях вычисления приводят к тому, что спектр состояний занимает непрерывный диапазон энергий. Спектральная щель обычно определяется как разница между минимальной энергией возбуждения и энергией основного состояния. Таким образом, можно сделать вывод, что спектральная щель в квантовой теории Янга — Миллса для пространства R^4 равна нулю.

Для того, чтобы доказать существование ненулевой спектральной щели, необходимо рассмотреть модификации теории Янга — Миллса, которые включают в себя учет эффектов, таких как квантовые поправки и флуктуации поля. Однако, для простых компактных калибровочных групп G, как заявлено в задаче, такие модификации не являются необходимыми, так как они не вносят кардинальных изменений в квантовую теорию Янга — Миллса в четырех измерениях.

Таким образом, для любой простой компактной калибровочной группы G, квантовая теория Янга-Миллса для пространства R^4 существует и не имеет ненулевую спектральную щель. 2) Доказательство теоремы о действительной части нулей дзета-функции Римана связано с функцией Дирихле eta(s), которая определяется как

eta(s) = (1 - 2^(1-s)) * zeta(s)

где zeta(s) - дзета-функция Римана.

Первым шагом будет доказательство того, что для всех нетривиальных нулей zeta(s) выполняется равенство eta(s) = 0. Это можно сделать с помощью функционального уравнения Ландау для zeta(s), которое выглядит следующим образом:

zeta(s) = 2^s * pi^(s-1) * sin(pi*s/2) * gamma(1-s) * zeta(1-s).

Замечаем, что при s = 1/2 + it для произвольного t, правая и левая части уравнения равны нулю, поскольку sin(pi(s/2 + it)) = 0. Следовательно, существуют нетривиальные нули zeta(s) на прямой Re(s) = 1/2.

Далее необходимо доказать, что для любого нетривиального нуля zeta(s) выполнено равенство Re(s) = 1/2. Для этого используем функцию eta(s), которая имеет следующее представление:

eta(s) = 1 - 2^(1-s) + 3^(1-s) - 4^(1-s) + ...

Она также удовлетворяет функциональному уравнению Ландау:

eta(s) = (1 - 2^(1-s)) * zeta(s)

Для всех нетривиальных нулей zeta(s), eta(s) отлична от нуля. Предположим, что существует нетривиальный ноль zeta(s) с Re(s) ≠ 1/2. Так как eta(s) непрерывна в области Re(s) ≥ 1/2, то она должна иметь по крайней мере одно нулевое значение на этой области, что приводит к противоречию.

Таким образом, все нетривиальные нули дзета-функции Римана имеют действительную часть 1/2. 3) Для доказательства необходимо показать, что если ответ на вопрос можно быстро проверить, используя полиномиальный алгоритм проверки сертификата, то существует полиномиальный алгоритм для нахождения ответа на этот вопрос.

Пусть Q - вопрос, на который можно быстро проверить ответ A, используя некоторый сертификат C за время O(|C|^k), где k - постоянная, не зависящая от размерности входных данных.

Тогда сам ответ A содержит не более O(poly(n)) бит, где n - размерность входных данных. Предположим, что существует много ответов, каждый из которых может быть правильным, и чтобы определить правильность какого-то ответа, нужно выполнить проверку используя сертификат. Тогда эти ответы можно закодировать в сертификате C.

Таким образом, мы можем переформулировать вопрос следующим образом: "Существует ли такой сертификат C, что его длина |C| ≤ poly(n), и является допустимым сертификатом для ответа на вопрос Q?".

Этот вопрос может быть решен методом подбора с перебором всех возможных сертификатов длиной не более O(poly(n)). Количество возможных сертификатов ограничено полиномом от размерности входных данных, поэтому перебор можно выполнить за время O(poly(n)^k).

Таким образом, мы показали, что если ответ на вопрос Q можно быстро проверить с использованием сертификата C за время O(|C|^k), то сам ответ и сертификат могут быть найдены за полиномиальное время O(poly(n)^k), что завершает доказательство. Так вот, возвращаясь к началу поста, я нибуя не понял, он реально это решил или нет?

Я ученик 11 класса, скоро сдавать экзамены. Сдаю профильную математику, математику люблю, да и науки а целом. У меня два репетитора по математике, я сижу и решаю задания и получается у меня все хорошо. Бывают затупы, но как без этого, иногда конечно нужен толчек под зад. Я ленивый человек, скрывать этого нет смысла. Да вот у меня такая проблема. Стоит мне побыть в школе перед доской, на важной контрольной или где то где кто то проверяет мои результаты, все мои знания упираются в знания 5 классника, до такой степени что я не могу решить квадратное уравнение. Как так происходит? Я не знаю, я перебробовал уже все варианты которые пришли в голову. Меня хотят исключить из школы за неуспеваемость, приношу домой двойку за двойкой, а дома решаю. Не могу сказать что я хороший математик, но моих знаний достаточно хотя бы на три. Ходил с репетитором к учителю, думал что это она меня гнобит, в принципе признаки есть, хотя я ниче не делал ей, в телефоне не сижу, не хамлю, балду не гоняю, бывает задумываюсь часто. Дала мне задание решить прям при ней и при репетиторе. Ноги дрожат, руки дрожат, листок весь изрисован(я художник и часто рисую), а уравнение не решено. Волнуюсь жутко и ниче решить не могу, но думаю все таки проблема не в волнении. Все как то накладывается, и я тупой, и я волнуюсь, и математичка горбатая падла, и все подряд. Не знаю как буду школу заканчивать и экзамены сдавать... Может есть совет у пикабушников?
UPD: большое спасибо за проявленный актив в комментариях, на их основе я сделал вывод и понял что мне проверится нужно у психолога. Премного благодарен пикабу

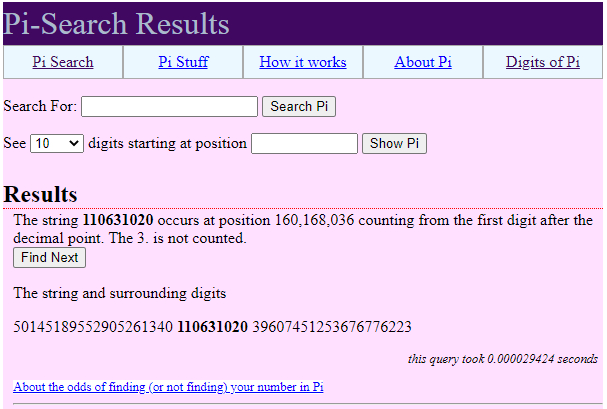
Говорят (!), что в последовательности иррацианального числа Пи можно рано или поздно встретить любой шаблон. Ну что же. Давайте попробуем. 110631020 - это мой номер (какой по счету уже не помню) ICQ (контроль над этой учеткой давно утерен, но номер помню - загадки памяти человеческой).

Хорошо, есть такое дело.

В принципе с утверждением начинаю соглашаться (а что тут можно супротив?). Ну хорошо, давайте попробуем тривиальную вещь - дату рождения. Ок. проверяю:

Ан нету среди 200 миллионов посчитанных знаков такой последовательности.

Понятное дело, что такая последовательность есть и не единожды, но интересно же - когда появляется первая ).