Как начать 3д печать. Топология? Кто такой «Топология»? Зачем она мне?1
Когда я начинал путь в 3д, возникало много вопросов. Но не всегда удавалось находить ответы. В первую очередь, потому что я не знал какие вопросы надо задавать.
Попробую постепенно их разобрать.
Поскольку начинал я с САПР/CAD (система автоматизированного проектирования/computer-aided design), то не мог понять почему все постоянно говорят про «сетку». Нет, я знал, что она есть. Но зачем она нужна именно мне? Почему это так важно?
А это и не важно! Если ты занимаешься проектированием деталей – она тебе не нужна. Нет, ну не то чтобы совсем не нужна, но, в целом, можно пренебречь. Почему?
На картинке в начале поста, вы можете видеть 3 состояния одного объекта.
Первый – куб из CADа (Fusion 360). В том виде как я его нарисовал.
Второй – из Blenderа. В виде набора полигонов.
Третий – экспорт из Фьюжена в STL формат. Открыл его в Блендере.
В процессе экспорта произошла триангуляция. Триангуляция – процесс разбиения полигонов на треугольники.
КАДы работают с твердотельными объектами, а программы вроде Blender, 3D Max, Cinema 4D – работают с мешами. Mesh – та самая сетка. А ещё КАДы оперируют математическими формулами, и им пофигу на сетку, им важны размеры.
Сетка состоит из полигонов. Полигоны состоят из вершин(vertex), и соединяющих их граней(edge).
Обычно полигоны состоят из четырёхугольников. В некоторых случаях – из треугольников. Есть ещё многоугольники(n-gon). Четырёхугольники любят, это наши бро. Треугольники используются в игровых движках, слайсерах (мы же тут про 3д печать, да?), ну и где-то ещё. Это тоже бро. А энгоны – не бро! Они приводят к артефактам, нарушениям топологии, сбоям в работе модификаторов, и проблемам при текстурировании.
Важное замечание: иногда невозможно избежать многоугольников в сетке, а иногда они ни на что не влияют. Но всё же их лучше избегать.
Так вот! К чему это я? Когда мы перегоняем модель из формата в формат, программа сама решает, как переводить твердотельную модель в полигональную. И вам может не понравиться решение, которое она приняла.
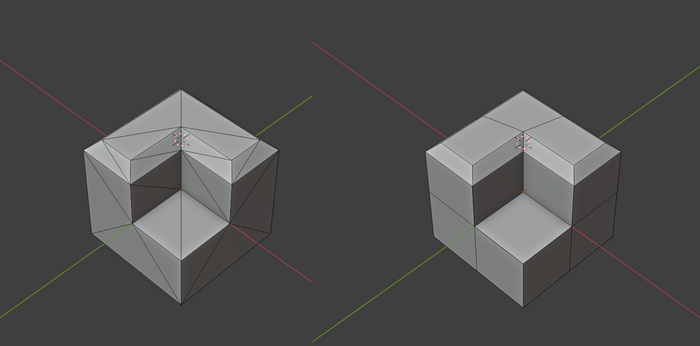
Например, тут наложены фаски. Слева – во Фьюжене. А справа – в Блендере.
Топология ещё сносная. Теперь накладываем модификатор Subdivision.
Первый вариант – то, что вышло из Фьюжена. Второй из Блендера. А третий вариант – то, что мы хотели получить. Так вот чтобы это получить – нам необходимо добавить грани поддержки. Только тогда наш куб сгладится как положено. Но в триангулированной версии куба, мы уже не можем этого сделать. Вся топология сетки порушена. Теперь ни один модификатор не ляжет так как вы ожидаете. Результат непредсказуем. Делать UV развёртку, на такой модели, и накладывать текстуры – тоже, то ещё развлечение. Я уж молчу про анимацию с деформациями.
Так он выглядит с поддержками, до применения модификатора.
Что мы имеем? Вы можете забить на любую топологию сетки. Ровно до тех пор, пока не решите сделать что-то с моделью. Текстуры, анимация, деформация. Всё это недоступно, если вы не следили за сеткой изначально.
Разумеется, есть решение: ретопология! Это когда вы ручками, или при помощи сторонних программ, пересобираете сетку. Т.е создаёте модель заново, поверх старой.
Или просто поправляете существующую. Иногда это может занять ооочень много времени.
Автоматизированный способ – часто не удовлетворяет всем требованиям. Но решать Вам.
Неправильная топология – одна из причин, почему вы не можете взять модель для печати, и анимировать её. С ней придётся долго работать. И часто бывает так, что проще отрисовать новую, чем проводить ретопологию старой.
Хотите ещё крипоты?
Угадайте что тут изображено!
Ладно. Хватит на сегодня. Пишите в комментариях темы, на которые нужны посты, постараюсь разобрать.
Всем бобра!