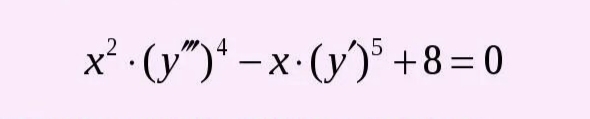А так выглядело до сборки

Что узнал занимаясь разработкой этого устройства:

-3д печать позволяет реализовать без поддержек функциональную резьбу

-если пружины то обязательно плоские и из PETG, а вот такие варианты как на изображении ниже ужасны особенное если они небольшого размера.

Видео для любителей ASMR)

Так получилось, не специально... эта штука недолго, но красиво светится в темноте) PETG был только такой под рукой.

К сожалению или к счастью, после того как я закончил устройство мне стали выдавать другой инфузионный набор в комплект которого уже входит установочное устройство, и эта вещь так и осталась неиспытанной. Все модели для ознакомления выкладываю на thingiverse.

Ну и куда без нейросетей?! Кстати девушка на видео врет, судя по тому какие крутые проекты делают товарищи из лиги 3д принтеров (последнее что видел был шлем с вентиляцией и камерами), я уверен, они бы справились лучше.

Сейчас же я вам постараюсь рассказать смысл этих дифференциальных уравнений (далее по тексту - дифф.ур) или же какую они играют важную роль в нашей жизни. А вернее - важную роль при развитии современных технологий, цифровизации и т.п.

Сразу скажу, что я не прям математик и отличник, но постараюсь своими словами, свой логикой донести до вас своё представление.

По сути математика как и любая другая дисциплина позволяет взглянуть на наш окружающий мир с разных сторон, описывать его с разных взглядов, и поэтому каждый человек его воспринимает по-своему (кто к чему как говорится склонен). Математика в свою очередь позволяет описывать процессы, явления в этом мире в виде формул, в виде каких-либо закономерностей, показывать вероятность событий в числах, собирать статистические данные и осуществлять прогнозирование и т.д.
И в первую очень это нужно тем, кто двигает прогресс, кому нужны расчеты и исследования (научные кадры, инженеры).

Если же обычные уравнения описывают простые статические закономерности, например:
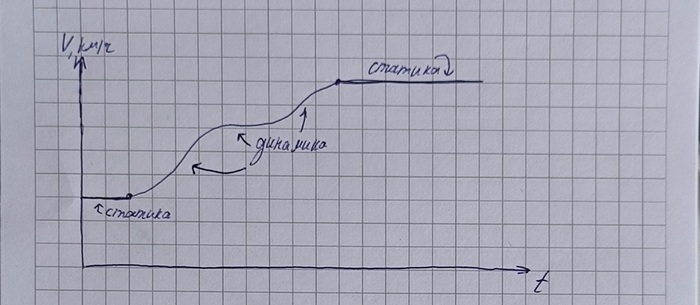
простая формула движения машины (т.е. через сколько времени ты приедешь к пункту назначения, выдерживая постоянную скорость);
или радиальная скорость вращения минутной стрелки (т.е. через 60 секунд минутная стрелка сместится на 360/60 градусов).

То дифференциальные уравнения позволяют описывать систему ЦЕЛИКОМ (в идеале конечно же), т.к в жизни имеются переходные процессы. Соответственно, когда заходит речь о динамике - статистические уравнения становятся сложнее, приобретая вид дифференцированных. Суть переходного процесса заключается в том, что мы переходим от одного статического положения к другому статическому.

Например (№1), ехали с одной скоростью (статическое движение), разогнались до другой скорости и продолжили ехать дальше с новой установленной скоростью (снова статическое).

Хотя в жизни это практически никогда не случается, ибо любое внешнее воздействие выводит систему из равновесия.

Простой пример (№2). Небольшая горочка или ямка, небольшой перевозимый груз или плохое топливо, тепло на улице или холодно (как внешние факторы) хотя бы минимально, но будет влиять на скорость машины, на расход топлива, на температуру двигателя, и эти процессы в real life никогда не будут статичными, и всему этому в математике как раз дается описание этим явлениям в виде дифф.ур. А организм - это вообще целый ансамбль переходных процессов внутри человека (динамичный и попрой непредсказуемый, биохимия и образ жизни дают о себе знать).

Так вот вернемся к дифф.ур. В одном дифференциальном уравнении зашито БЕСКОНЕЧНОЕ количество обычных уравнений, поэтому я и сказал ранее что дифф.ур. - это описание ЦЕЛОЙ СИСТЕМЫ, которая будет зависеть не только от НАЧАЛЬНЫХ УСЛОВИЙ, но и иметь какие-то свои КОЭФФИЦИЕНТЫ, которые будут охарактеризовать динамику переходного процесса (резкость графика функции, её крутизну, импульсивность и т.д).

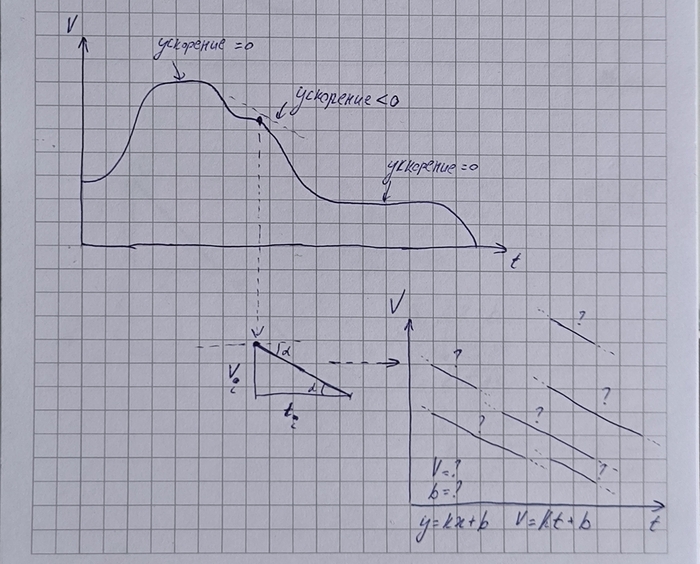
Пример (№3). У нас есть график скорости машины (зависимость скорости от времени). Найдя производную в одной какой-нибудь точке, можно определить тем самым ускорение машины (конкретно в тот момент времени). Величина ускорения при этом будет охарактеризовываться величиной угла наклона касательной к оси х в этой точке. Но найдя первообразную этого же ускорения, выполняя тем самым обратное действие (как это делается при решении дифф.ур с нахождением интеграла), мы сможем построить ТОЛЬКО линейный график функции.
И что нам потом этот линейный график даст? Да ничего путного! Это просто прямолинейный график, в котором мы знаем только угол наклона, который можно построить где угодно на плоскости, на любой высоте (относительно координаты х и y).

Поэтому при решении дифф.ур (при нахождении интеграла) появляются как раз те самые непонятные константы (С), которые гласят о том, что уравнений может быть бесконечно, и эти константы позволяют (если рассматривать данный пример) устанавливать конкретное положение прямой на графике.

И теперь для того, чтобы попасть в нужную нам исходную точку, нам необходимо найти эту самую константу, а для этого потребуются исходные данные (начальные условия) в виде скорости V и времени t в исходной точке. Попадая в эту точку, мы находим частное решение (уравнение со всеми известными коэффициентами). Что нам может дать это частное решение в данном случае? Спрогнозировать какая будет скорость за ближайшее время (в данном случае это через 1-3 секунды). Но как вы понимаете, это далеко не точные данные, т.к. первоначальный график был не линейный, а хаотичный. С помощью одной проведенной такой процедуры мы не построим исходный график движения, мы лишь его охарактеризовываем только в один какой-то конкретный момент времени.

Какой мы можем сделать из этого всего вывод. Общее решение дифф.ур. — это когда мы находим бесконечное количество уравнений у системы, а частное решение — это когда среди всех полученных уравнений мы находим то самое, которые нам нужно исходя из начальных условий.

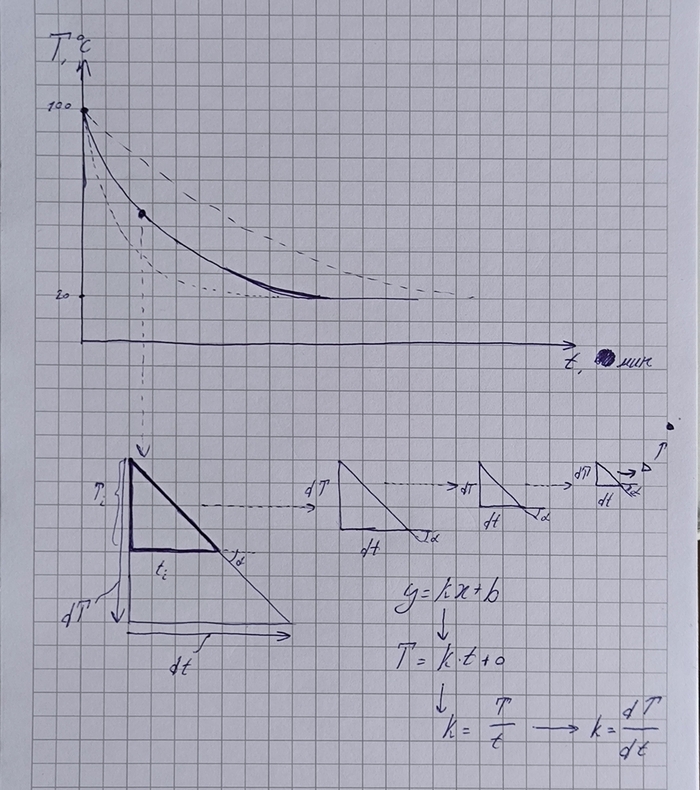
Теперь для наглядности продемонстрирую самое настоящее дифф.ур. на простом бытовом примере. По каким законам у нас происходит остывание воды в кружке? Как вы понимаете, этот процесс не линейный и к тому же зависит от множества внешних факторов.
В качестве таких внешних факторов выступают как минимум: объем воды, теплоёмкость жидкости (молока, воды, киселя), конвекция воды (соответственно накрыта ли кружка блюдцем или нет), испарение (влажность в комнате), теплопередача кружки (фарфор, пластик, алюминий), температура комнаты, площадь поверхности, и т.д. Под последним подразумевается, что если мы перельем горячую воду из кружки в противень, то она остынет намного быстрее, т.к. она растекается по большой площади.
Поэтому чтобы описать процесс одним простым уравнением (не дифф) - нужно соблюсти ВСЕ вышеуказанные внешние условия, и подобрать все подходящие коэффициенты, но это как вы понимаете практически нереально. Поменяется чутка объем - закон изменения уже будет немного другим, а это соответственно новое уравнение.
Так вот вся эта система будет описываться следующим уравнением:

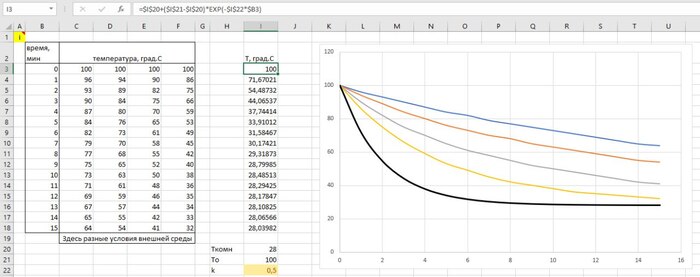
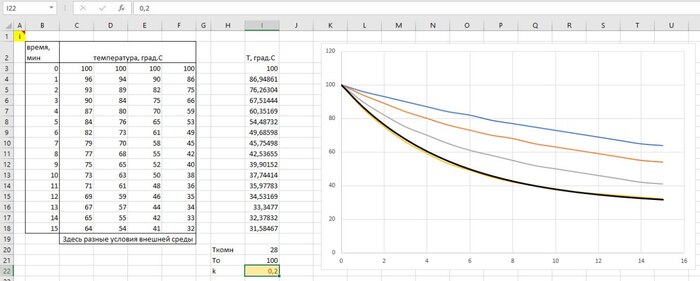
dT/dt = -k(T-Tкомн)

Как я читаю это уравнение: "изменение температуры dT по изменению времени dt (или же скорость изменения температуры) равно крутизне графика", где "показатель крутизны зависит от коэффициента k и разницы между температурами". Другими словами, чем больше разница между температурами, тем круче будет график и тем быстрее значит остынет вода и наоборот. Поэтому приближаясь к комнатной температуре вода начинает остывать очень медленно.

Что такое dT/dt?
Буква d - означает ПРОЦЕСС изменения (в моём понимании).
Если мы просто проведём касательную к графику и достроим треугольник, то угол наклона как раз будет описываться коэффициентом T/t, что соответствует прямой y=kx+b, где b мы принимаем за ноль (т.к высота графика относительно оси y не влияет на данный анализ), y - это температура Т, х - это время t.
Теперь давайте попробуем визуально начать увеличивать треугольник, и как вы понимаете процесс его увеличения никак не влияет на этот коэффициент T/t, т.к пропорции треугольника остаются прежними, и угол остаётся тем же. А если наоборот его уменьшать до бесконечности? Всё равно даже у этого милипи*дрического треугольника, у которого стороны T и t стремятся к нулю, пропорции останутся теми же, угол будет тем же, и коэффициент соответственно не поменяется и будет тоже прежним. И вот как раз этот dT/dt и охарактеризовывает угол наклона графика относительного этого достроенного маленького до бесконечности треугольника (если это можно так выразиться в простых словах). Т.е., другими словами, dT/dt - характеризует угол наклона графика в той самой точке.

Теперь просто вбиваем написанное выше уравнение в калькулятор и выводим результат (нет смысла изъё*ываться ручным счетом). Как решается это дифф.ур. — это не про данную статью, это уже целый курс по высшей математике, расписывать здесь не вижу смысла, я передаю лишь смысл этого всего. Итак, получаем решение

T(t) = Tкомн + (С)*e^(-kt) - экспоненциальная функция

Как выводилась "е" в математике - это тоже другая история. Сейчас это нам не интересно.

И вот у нас из одного диф.ур, описывающего систему, получается множество раличных уравнений, зависимых от времени t, коэффициента k и константы C. Другими словами - уравнение с параметрами.

В качестве константы C у нас будет (To - Tкомн) - в физике это, кстати, будет называться перегревом, где Тo — это температура в нужной нам точке (в той точке, которую мы хотим выбрать для расчета, например 90град.)

Зная все необходимые данные, мы можем построить точную зависимость остывания воды для конкретного случая. И затем можем уже решить простое уравнение в любой точке (любого момента времени t).

И если с константой С, комнатной температурой Ткомн и временем t всё понятно. То, как теперь, собственно, найти ту самую k, зависимую от множества раннее указанных факторов??? Самый простой способ — это провести лабораторную работу у себя дома - измерить температуру естественного остывания воды. Нам лишь нужны точки (замер температуры) в разный момент времени (t = 0, 1, 2, 3 ... 30 мин).
Без этих точек у нас не получится вывести дифф.ур.

Все просто: Измерили, забили точки в эксель, построили эмпирический график))

Далее строим второй график только уже не по измеренным данным, а по формуле, указанной выше. Подставляем те же t, а коэффициент k подбираем вручную, чтобы теоретическая зависимость максимально повторяла экспериментальную (эмпирическую).

Теперь повторяем эксперимент с разными кружками, с разным объемом, с блюдцем / без блюдца, подбираем тем самым коэффициент k на все случаи жизни.

Поздравляю! Вы построили тепловую модель остывания воды!

Теперь вы можете не пользоваться термометром, а лишь рассчитывать температуру воды в любой момент времени когда захотите.

Делать конечно же это на постоянной основе вручную и при этом отслеживать тайминг — это само-собой очень муторно и очень неудобно. Однако подобные тепловые модели позволяют избавиться, к примеру от лишних датчиков в различных системах, или же сравнивать расчетные данные с реальными (фактическими), ведь компьютер способен в режиме реального времени производить мониторинг системы, выполнять более миллион операций/вычислений за долю секунды, для компа это не сложно, компу нужны лишь алгоритмы и заданные условия, для этого, собственно, предусмотрены специализированные ПО.

То, что я привёл выше - это лишь сааааамое простое диф.ур, которое имеет только отдалёёёёённое приближение к реальности. На деле же эта система будет выражена в более сложном виде, и скорее всего она будет описываться диф.ур. 2-го или 3-го порядка, система, которую невозможно будет описать в максимальной точности. Все, потому что невозможно в реальной жизни учесть прям все-все влияющие факторы и представить это в виде одной буквы k, как это сделал я для наглядности. В свою очередь эти коэффициенты k в жизни (как ни странно) ТОЖЕ динамичные! И они состоят из множества других коэффициентов, которые по-хорошему надо описывать законами физики /научно-обосновывать, а не тупо подбирать вручную. Поэтому представленное в данной статье дифференциальное уравнение описывает в ПРОСТОМ ВИДЕ систему остывания воды. И описать систему мы можем только в очень приближенном виде.

Так, где же ещё применяются дифф.ур.? Да на самом деле много где:

Расчеты электронных схем, в которых используются конденсатор, катушка, аккумулятор (т.к. эти элементы являются накопителем энергии)

Расчеты тепловых процессов (в двигателях, устройствах, в той же электронной схеме)

Расчеты нагрузок и моментов (в строительстве и проектировании)

Имитация жизненного цикла элементов, приборов, конструкций

Гидродинамика и аэродинамика

Динамичные процессы (разгон двигателя)

Картинки если что я просто в инете взял (не я рисовал)

В общем дифф.ур. позволяют моделировать процессы сложных системах, которые зависят от многих факторов, от начальных условий, процессы, которые можно максимально близко привести в соответствии с реальностью, но не повторять их в точности.

Надеюсь было интересно и полезно)