Представьте себе: Базиль сто раз подбрасывает монетку, и каждый раз выпадает орёл. Это нормально?

Да быть такого не может! Либо у нас избирательная слепота на решки, либо монетка фальшивая - с двумя орлами.

В целом естественнее получать что-то поравномернее. А почему так?

Обозначим орлы орлами (вернее, ноликами) и единицами решки. И сложим все результаты по сотне подбрасываний. ЦПТ (центральная предельная теорема) утверждает: "чем больше подбрасываешь, тем ближе будешь в среднем арифметическом к одной второй". Одна вторая - матожидание для равновесной монетки (где вероятность выпадения и орла, и решки именно 1/2).

В этом смысле сотня орлов подряд - дикое отклонение.

С точки зрения суммы, бесспорно, сто решек подряд - это нонсенс. Но почему мы считаем именно сумму?

Вычислим знакопеременную сумму: х1 - х2 + х3 - х4... В этом случае как сотня решек подряд, так и подряд сто орлов будут вполне себе матожидаемыми результатами. А уникальными отклонениями станут "ОРОРОР...ОР" и "РОРОРО...РО".

Что вообще происходит?

Где-то там выше мы не случайно ввели числовые обозначения (орёл и решка -> нолик и единица). Мы теперь можем результат испытаний прочесть как вектор. Стомерный вектор, дело обычное. Очередная вершина стомерного кубика с единичным ребром.

Если мы сделали ровно одно испытание, у нас отрезок вариантов (вернее, концы отрезка: по Ох отметим 0 и 1).

Если мы сделали два испытания кряду, их результаты - это (0;0), (0;1), (1;0) и (1;1), т.е., вершины квадратика, уже на плоскости.

Если три испытания - вершины детского кубика с динозавром и буквой Ю.

Ни одна из вершин полностью симметричного кубика уникальной априори не будет. Следите за руками: берём агрегатную функцию "сумма координат" (линейная функция, постоянная на гиперплоскостях, перпендикулярных направлению главной диагонали, растущей из начала координат, т.е., вектору из сплошных единиц), считаем вершины кубика с одинаковым результатом по этой вот агрегатине, а потом заявляем: ну ой, тут две уникальнейших точки выдались (начало координат, где сплошные орлы, и ровно напротив конец главной диагонали, где одни решки).

Что нам мешало взять другую диагональ? Или вообще не диагональ. Там дофига разных векторов, спроецируем на любой.

Собственно, почему "сплошные орлы" выглядят удивительно? Потому, что подспудно мы сравниваем не с конкретной другой последовательностью, а с набором других: "вероятнее получить что-нибудь равномернее", где этих вот "равномернее" у нас мешок.

В магазине стоит большой ящик картошки. Вы берёте оттуда одну картофелину, откладываете, дальше набираете целую сумку картошки. Переносите в другое место, вываливаете там где-то всю сумку, и тот первый клубень. А берёте одну картофелину. Какова вероятность, что вы скорее взяли нечто, что несли в сумке?

Сравните с утверждением "получить цепочку из сплошных орлов менее вероятно, чем цепочку с чётким чередованием орлов и решек". Или "чем ОРООРРОООРРР..." (одна, одна, две, две, три, три и т.д.) Собсно, каждый отдельный заданный результат, индивидуально, столь же невероятен, как и сплошные орлы.

Каждый отдельный заданный результат из ста испытаний имеет вероятность... вероятность... 1/2^100. Давайте прикинем, что это. Двойка в десятой чуть больше тысячи. В тридцатой - чуть больше тысячи в кубе, т.е., миллиарда. В сотой больше, чем в девяностой, а в девяностой больше, чем куб миллиарда. Одна миллиардная в кубе - вот (в грубой нижней оценке) вероятность получить любую заранее заданную - одну конкретную - последовательность из ста орлов и решек. Любую, а вовсе не только "сплошные орлы".

Ясно, что с точки зрения многомерного кубика ни одна из его вершин не особенная. Но получается так, что в привычной проекции (на главную диагональ из нуля и подобные) образуется очень не равномерное распределение точек по целевому отрезку.

Мне любопытно было узнать, а есть ли другие проекции? На других направлениях, более, так сказать, натуральные для таких кубиков? Чтобы как-то поравномернее получалось, или совсем равномерно? Чтобы проекция помнила все точки лично, а не какую-то агрегатную функцию, типа суммы координат?

Аналогичный вопрос для игральной кости (там исходно многомерные кубики со значениями координат от 0 до 5 - это ребро длины пять, а не шесть, замечу).

Название поста отсюда: многомерная штука с кучей узлов, в форме кубика, это типа кусок многомерной авоськи. Чтобы носить в ней бутылку Клейна, или проекции брать на различные направления.

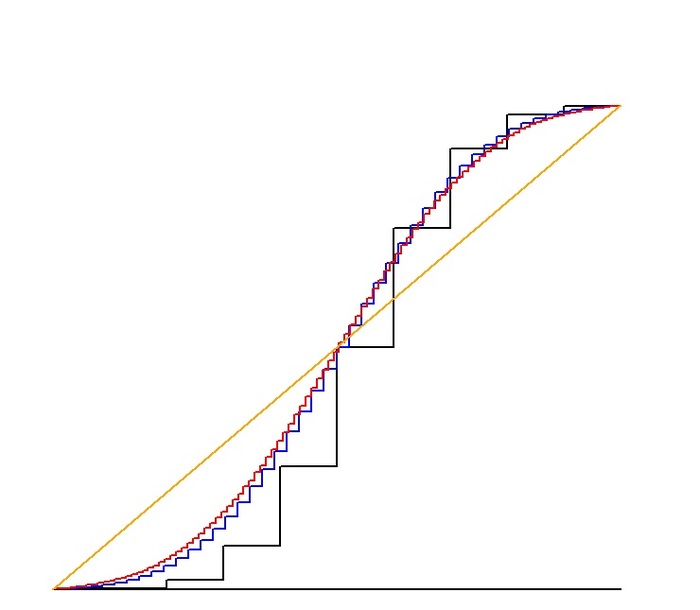
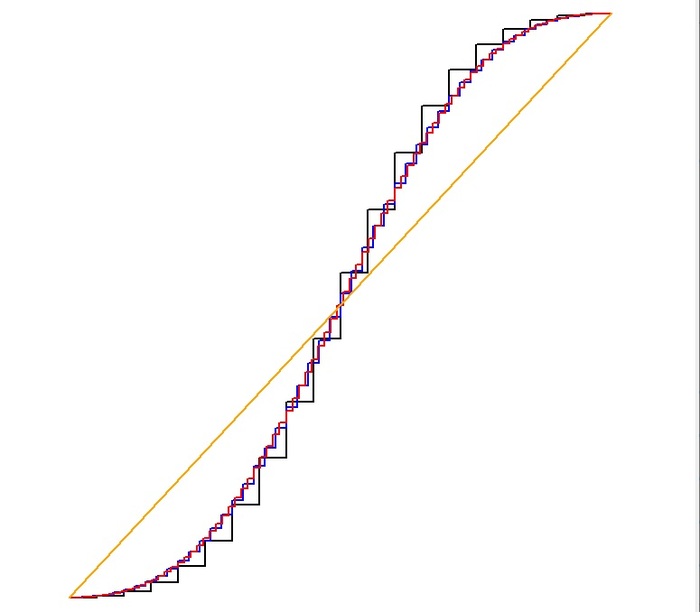
Я посчитала и для монетки, и для игральной кости случаи "проецируем на вектор из сплошных единиц / вектор из натуральных чисел подряд / вектор из простых чисел подряд / и ещё там один". Делала следующим образом: собирала массив из скалярных произведений вершин с целевым направлением (на кого проецируем), упорядочивала по возрастанию, нормировала. Дальше строила графики типа интеграл плотности распределения: чёрный - по проекции на вектор из единиц (т.е., сумма координат), синий - на вектор из натуральных подряд, красный - из простых чисел подряд, а оранжевый - я пока не скажу.

Главное, на оранжевом - равномерное распределение.

Зацените глюковину: можно авоську Клейна спроецировать на такой вектор, что в результате получится равномерная плотность. Без вообще какой-либо потери в данных (в отличие от убогой суммы координат).

Комментарий к картинкам: почему всего девять подбрасываний монетки и лишь четыре подбрасывания игральной кости. Ну потому что получаются большие массивы данных, и довольно высокие графики даже при шаге вверх на полпикселя. Не помещалось в экран, короче. Ну или так помещалось, что ничего по делу там уже не разглядишь.

Внимание: кто придумал, что за оранжевый вектор, я вам специальный камент сделаю к этому посту - чтобы там можно было бы написать "я придумал!!!" Только ответ пока не пишите - дайте другим помучиться, имейте совесть.

Как я вообще вот этим всем занялась. Я репетитор, по математике с информатикой. Но только по математике я ближе к алгебре - с чистой абстракцией мне возиться приятно, а вот с реальностью так себе. Ну и статистика, как я думала, мне не под силу.

В прошлом году, однако, сразу двое студентов (матано-линальных) стали очень просить, чтобы я с ними продолжила в этом году про матстат. Я сначала поотпиралась, но потом вдумалась - нафиг терять доходы (передавать их коллегам), и взялась разбираться. Ибо, в конце концов, теорвер для начала - чистая комбинаторика, это я всё же умела.

И накупила я себе тонну книжек про эту вашу статистику. И закопалась там, и людей доставала вокруг, до кого дотянулась. Кто хоть какие-то знания в этом предмете имел.

Ну так и вот. Мой вывод - это нормально не понимать. Ну потому что понять, почему главная диагональ многомерного кубика уникальна, нельзя. Нипочему потому что. Не уникальна, и всё, вот.

Заказать мягкого котика вы можете на aliexpress

или на яндекс маркете

Приглашаю вступить в моё сообщество