Перемена мест слагаемых6
Я бы тоже так решил. Идиотизм.
)))
Черт.. Ладно, ваша взяла. Я умею признавать ошибки. Вернее неспособность отстоять свою правоту. А я действительно прав ))
раскрыть ветку (1)
Ошибка в том что, метод, которым детей обучают умножению, вы воспринимаете как закон. Просто, если ребёнок сам сообразил, что можно поменять местами множитель и множимое, если он понимает что он умножает, неправильно говорить ему что это неправильно, что это ошибка, тем более если в дальнейшем окажется что это не было ошибкой. Я б на месте отца объяснил бы своему ребёнку все это, раз уж он сам с этим столкнулся, пускай раньше времени. Авторитет учителя пошатнется, да и хуй с ним. Я сам, с годами, вспоминаю школу и понимаю, процентов 70 из них тупые. Ах да, полез в Википедию на всякий случай, вдруг я ошибался
К сожалению некоторое количество комментаторов на Пикабу из всех арифметических действий владеет только навыками минусования. Но к счастью арифметике на них глубоко пох и вряд ли правила изменятся в обозримом будущем..
раскрыть ветку (25)
Арифметике пох на шарики и пеналы, она занимается числами, их свойствами и отношениями. И она говорит, что операция умножения является коммутативной, то есть a*b=b*a.
раскрыть ветку (20)
Боже мой, адекват в ветке. Я уж подумал, что тут все в какой-то параллельной реальности обучались, где их обучали складывать МАШИНКИ и ДОМИКИ, а не числа. Все эти машинки, шарики, ребятки - это же просто визуальная надстройка для детского мозга, чтобы ему легче было начать во всё это вникать!
Арифметика - это инструмент для решения простейших математических задач. Просто раньше в начальных классах предмет так и назывался. Но тем не менее умножали там не латинские буквы, а предметы.
раскрыть ветку (18)
Предмет не просто так назывался, а по названию раздела математики. А вы сейчас пытаетесь придумать свою арифметику со своими правилами, в которых умножаются не числа, в предметы. И эти ваши правила, которые "вряд ли изменятся в ближайшем будущем" появились не так уж и давно, лично меня учили по другим, в которых "от перемены множителей произведение не меняется".
ещё комментарии
Вот пример
https://www.liveinternet.ru/users/bo4kameda/post309427992
521. Из корзины брали по 2 яйца 3 раза. Сколько всего яиц взяли?
раскрыть ветку (14)
Ну все, под вашими неопровержимыми аргументами я готов признать что арифметика занимается умножением предметов. Осталось определение арифметики подправить в энциклопедиях и учебниках не для 1 класса.
И да - сильно сомневаюсь, что ученику решившему 521 задачу путем умножения раз на яйца за раз и получившему в итоге 6 яиц снизили бы отметку.
ещё комментарии
Можете не сомневаться, снизили бы. В наше время (конец 70-х) было с этим строго. И эти учительницы видимо хорошо учились в то время...
ЗЫ А еще не ЕГЭ все бочку катят, мол заставляет детей бездумно запоминать варианты. Вот пожалуйста, наглядный пример бездумного отношения к вроде бы казалось пустяковой проблеме. А с таких мелочей и начинается образование...
раскрыть ветку (7)
Ну, если под образованием понимать исключительно следование программе обучения нашего МинОбра - то, наверное и ЕГЭ неплох и учительница правильно учит. Только вот почему-то для этого свою математику приходится изобретать. И не только математику.
ещё комментарии
Да какая "своя" математика??? Учат элементарной логике. Чтобы быстро подсчитать количество вещей в N кучках придумали не слагать N раз, а запомнить простое правило умножения количества вещей в одной кучке на количество кучек...
раскрыть ветку (5)
Тебя, видимо, так учили, чтоб ты все таки наконец-то уже блять понял принцип умножения. Но, к сожалению, этим тебе выбили способность мыслить самостоятельно. И сейчас,ты эту схему по которой тебе объясняли, пытаешься выставить каким то незыблимым математическим законом. Позорище
У вас ещё и логика элементарная тоже в редакции МинОбра, видимо. По которой коммутативность у умножения до 6 класса отсутствует.
ещё комментарии
ещё комментарии
ещё комментарии
ещё комментарии
ещё комментарии
Их не берут а складывают, то бишь подсчитывают. Считать можно яйца, но не разы... Хотя ... есть варианты подсчитать разы. Были бы яйца ))
раскрыть ветку (3)
ещё комментарии
ещё комментарий
Почему можно считать только яйца? Это закон, конкурирующий с коммутативным законом умножения?
ещё комментарии
ещё комментарии
Числа там умножали.
Если научитесь умножать предметы, а не числа, подавайте на Нобелевку.
Или у Вас отсутствует способность к абстрагированию..
ещё комментарии
Не надо подавать на Нобелевку. Это обычное правило, которое впиталось с молоком уроками первой учительницы.
ещё комментарий
ещё комментарии
ну значит в будущем вот так "правильно" расставляя переменные они неплохо так поебутся над физическими задачками уже даже среднего уровня, а про уровень выше и олимпиадный я вообще молчу, а если не будут следовать такой же логике назревает вопрос: к чему все эти выебоны тогда?
раскрыть ветку (3)
Объясните мне, пожалуйста, физическую разницу между умножением 3 пеналов на 4 ручки/пенал и 4 ручек/пенал на 3 пенала. Спасибо.
раскрыть ветку (2)
ещё комментарии
Всё ясно. Это отучение от критического мышления и решения задачи несколькими, в том числе, нестандартными результатами. Всё должно решаться только одним, стандартизированным, "правильным" путём. Пусть даже результат правильный, но важнее, что он достигнут не по вбиваемой учебниками схеме.
раскрыть ветку (57)
Это было еще тогда, когда я учился. Если я предлагал свой вариант решения задачи, то учитель просто говорил, что я делаю не так, как проходили и ставил в лучшем случае 3. Выпуск школы 2005.
раскрыть ветку (6)
Учился ещё по советским учебникам, в которых по геометрии к каждой типовой задаче предлагалось несколько вариантов решения - графический, расчётный, прямой, от обратного и т.п. И была Ольга Николаевна, которая на уроке объясняла только первый способ и за решение задачи другим способом снижала оценку на балл. Какое счастье было, когда наш класс другому учителю передали.
раскрыть ветку (1)
Были доп оценки за нестандартные, олимпиадные, просто неизвестные нам тогда варианты решения задач. Выпуск 12 года, но классной и учителем математики была бабушка)))
раскрыть ветку (8)
раскрыть ветку (7)
Скорее всего, этот опытный учитель при проверке работ открывает страницу с ключами теста, и тупо ебашит по ним, отключая голову.
раскрыть ветку (1)
Тут одно из двух - либо просто редкостный долбоебизм, либо глобальный заговор с целью отучить детей думать самостоятельно, а мыслить только так, как прикажут
раскрыть ветку (4)
хз может надо было подписать что на что умножаешь, у нас так было в начальной школе, еще всегда учили в ответе подписывать. 12 чего блять? на поебалу на на. Галина Яковлевна, простите что забыл таблицу квадратов до 20 и синус угла в 30%. никогда не забуду как вы придумывали системы уравнений за 10-15 секунд, как рисовали голой рукой системы координат. И никогда не забуду ваше "решаем по Виленкину" Галина Яковлевна я тупой наркоман который в школу в 8 классе перестал ходить но до сих пор спустя 13 лет без запинки помню теорему Виета и формулу Герона, про дискриминант вообще молчу, разбудите посреди ночи у меня отскочит
Нет, там просто хотят, чтобы в подобных задачах сначала писали один множитель, потом другой (типа яблоки на коробки, а не коробки на яблоки), у меня в школе тоже такое было, запомнить довольно не сложно, но непонятно зачем это. И перемножение другим путем - это не какой-то нестандартный подход, это с их точки зрения просто ошибка. Не вижу в этом ничего критичного.
раскрыть ветку (16)
Переместительный закон
Правило. От перестановки множителей произведение не изменяется.
Может они хотят, чтобы с детства сноски на правила в ответ записывали, чтобы подготовиться к жестокому миру, где надо доказывать, что ты не верблюд?
ещё комментарии
раскрыть ветку (6)
раскрыть ветку (5)
раскрыть ветку (4)
А почему не наоборот? В умножении скаляра на вектор первым пишется скаляр. Понятно, что если вектор a умножить на 2 — это то же самое, что сложить его сам с собой, а записывается это как 2a.
ещё комментарии
То, что ты написал - это и есть
отучение от критического мышления
Непонятно только, почему твой комментарий начинается со слова "нет", если ты обосновываешь то же самое.
ОМГ, ещё один. Где ты тут увидел два множителя чтобы писать сначала один, потом другой. Множитель здесь только один, другое число - множимое. Множитель по определению стоит вторым.
Здесь никто не оспаривается перестановку слагаемых. Здесь идёт речь про величины. Нехуй умножать пеналы на множитель, когда тебя просят найти яблоки. Хорошо выёбываться пока у тебя в задаче есть всего две величины. А когда их 20, половина из них комплексные и ты параллельно решаешь векторную задачу.
раскрыть ветку (6)
Вот блять и повыростали (или нет) долбоебы, которые верят в хуету про множитель и множимое.
Я тебя сейчас короче удивлю, но независимо от того, в каком порядке ты умножаешь - ты умножаешь пеналы на количество яблок в пенале. И при этом пеналы у тебя сокращаются. Курс физики, 7 класс. Ну типо знаешь, когда ты считаешь массу, то тебе похуй умножать плотность на объем, или наоборот. Всё равно в итоге кг выходят.
Офк во втором классе это знать рано, но суть в том, что именно ты несёшь полнейшую хуету. Хорошо выебываться, когда у тебя мозг не забит лишними знаниями. Ещё и какую-то хуйню про комплексные величины приплел, чтоб умнее выглядеть.
Блин, выебоны зашли слишком далеко. Вот что значит твой комментарий? То что ту фигню которую ты написал будет легче решать с твоим множимым и множителем? Серьезно? Давай для начала разберемся. Мы решаем векторную задачу (я тут не понял смысла слова параллельно, если мы решаем две задачи одновременно, то опять же, нафига? Так-то любое действие можно сделать в разы сложнее, если параллельно делать еще одно, "Вот легко тебе чистить зубы водя щеткой по часовой, а вот когда у тебя щетка из железа и ты в на центрифуге под наркотой катаешься...") и в этой задаче мы встретились с тем, что нам надо перемножить 20 множителей, половина из которых комплексные, для начала опять же вопрос, что это блин за векторная задача с комплексными, ну да ладно, мы тут все известные математики, мало ли что нам может встретиться, поэтому как-то к обычной плоскости добавилась комплексная. И тут самое интересное, нам эти все множители нельзя компоновать или сокращать, а нужно именно их все последовательно умножать на множимое? Так что ли? То есть если у тебя есть те же комплексные (a-ib) и (a+ib), а множимое это условно (a^2+3bi-c^3+di), то ты не можешь скомпоновать 2 множителя в простой (a^2+b^2), ибо это неудобно, гораздо удобней конечно наплодить в множимом 16 слагаемых от перемножения. Браво. Короче ребят, множимое - это ересь, не надо путать себе голову.
Вот только в умножении оба аргумента будут множителями независимо от размерности, а само умножение для чисел, даже комплексных, коммутативно.
И кстати, если уж придираться к тому, что перемножается, то у вас ошибка - нефиг как раз умножать яблоки на что-то, когда дано Х пеналов и У яблок/пенал
раскрыть ветку (3)
раскрыть ветку (2)
Это, конечно, аргумент. Ведь в младшей школе только их и перемножают, как всем известно
раскрыть ветку (1)
Ну в общем оценку снижать — это всё равно бред. Ответ и действие же правильное. Но можно было бы устно поспрашивать потом этого ученика, чтобы проверить, понимает он смысл действия или нет.
ещё комментарии
Вобще-то, к критическому мышлению этот случай отношения не имеет, это абстрактное мышление, когда перехдя на более высокий уровень абстракции игнорируются несущественные детали и производятся обобщения.
А во втором классе еще абстрактное мышление у детей не начинает развиваться. Так что раньше четвертого-пятого класса эту тему не надо затрагивать.
раскрыть ветку (2)
Ага, цифры они понимают, а абстрактное мышление только через 2-3 года завезут... Одно слово - учителки...
Нам наша математичка говорила что ей не интересен результат, ей важно как ученик решил пример. Потому часто примеры без решения а только с ответом она либо не засчитывала (касалось известных всем отличников образования то есть двоечников и троечников), либо заставляла объяснить как получился такой ответ. И, конечно, фигни с перестановкой слагаемых/перемножаемых величин не было.
раскрыть ветку (3)
Охохо, наша последняя была ОЧЕНЬ заинтересована в пути решения задачи. Нужно было расписать в мельчайших подробностях каждое действие. Я понимаю, что так проще отловить ошибку и поставить адекватную оценку, но как же заёбывало изводить по полтетради (на 48 листов) на одну домашку. Я с ней еще тогда обсуждала - что вот, вот это я делаю в уме, потому что могу, потому что это элементарно для старших классов. И всё равно - нужно расписать абсолютно всё и ниибёт.
раскрыть ветку (2)
Это всё же какая-ни-какая защита от списывания. Вы такая одна на весь класс могли быть, а списывальщиков треть потока.
раскрыть ветку (1)
Фигня это. Можно и переписать, хоть и больше времени уже нужно, и попросить за тебя сделать. К выпуску с математикой дружили минимум 5 человек, с кем-то да договоришься.
Любимая фраза нашей математички в школе (заслуженый препод ссср и рф, завуч школы) - "Думать вместе со мной". Спустя 11 лет все еще преподает..
Хз, у нас в инсте препода ответ вообще не волновал. Ты мог даже не писать его. Ему было важно порядок действий и формула. А то что ты где то попути мог ощитаться - его никак не колышило
Ничего, в другой ветке плюсов накидали тому, кто возмущался странным подходам "нас такому не учили", запутали, нахера....
Не стоит делать поспешные выводы
Вы про чё? Тут только перемена мест множителей и всё. Какой ещё способ? Второй написан - сложением.
Наоборот. Это учит понимать смысл действия. 5 пеналов по 3 ручки, а не наоборот. Т.е. нужно понимать смысл умножения. Это требуется, только когда непосредственно изучают умножение. Потом уже все равно.
раскрыть ветку (2)
Это может научить только тому, что вокруг много идиотов.
5 пеналов по 3 ручки вы получите 15 пена*ручек
по 3 ручки в 5 пеналах = 13 ручко*пеналов
А все почему? Потому что долбоебы! Во-первых в министрах долбоящеры вороватые, во-вторых на местах - долбоклюи тупорылые и в-третьих родители в подавляющем большинстве - долбоебы обыкновенные с отсутствием критического мышления.
Один из множителей - безразмерная единица. А вот место его нахождения в уравнении - нормальным людям побоку, а вот для долбоебов - до усрачки спорить будут, в том числе используя свое положение. Не замечая очевидных ошибок при этом.
Можно умножать и так: возьмём из всех пеналов по одной ручке, получим 5 ручек, затем ещё по одной и ещё по одной, получим 5+5+5 = 15 ручек, после чего ручки в пеналах кончатся. Записать в виде умножения это можно как 5·3
А каком критическом мышлении идёт речь здесь? им объяснили как делать, условие просто не выполнено.
ещё комментарий
Мне кажется это зависит от конкретного учителя. У моих детей в школе такого не случалось. Старшая закончила 11классов, средняя в 8м, младшая в 5м.
Есть тут учителя? Может разъяснит кто?
раскрыть ветку (70)
Не учитель, но объяснение простое. В младших классах работа на логику, абстрактные вычисления не берутся. Поэтому учитель проводит следующие рассуждения для умножения: сложить X предметов Y раз. Итого получаем для примера из поста следующие утверждения: (4 * 3) взять 4 ручки 3 раза = 4 ручки + 4 ручки + 4 ручки = 12 ручек. Ответ ученику не засчитан, поскольку логика у него сломалась: (3 * 4) взять 3 пенала 4 раза = 3 пенала + 3 пенала + 3 пенала + 3 пенала = 12 ручек пеналов.
И тут так же, надо взять 2 шарика 5 раз, чтобы ответ был в шариках.
Работа на абстрактные вычисления идет в следующих классах, где уже учат, что множители можно переставлять как угодно. В остальном учитель может следовать методичке или не следовать, но такие правила есть для вторых классов.
раскрыть ветку (66)
раскрыть ветку (17)
Посмотрите на формальное определение умножения в математике: a * b = a + a + a ... + a, (b раз). Поэтому если вы берете 4 ручки 3 раза, то строгая математическая операция будет 4 * 3. Даже название множимое (что?) и множитель (сколько раз?) об этом говорят. Только потом вы используете абстрактную математику и уходите от этих понятий на более высокий уровень.
Переместительное свойство объясняют потом так:
взять 4 ручки по 3 раза = взять 3 ручки по 4 раза
4 * 3 = 3 * 4
a * b = b * a
После этого можете воротить что хотите и как хотите, но пока дети этого не узнали, к ним во втором классе вот такие требования. Точно не скажу, но вроде к концу второго или в третьем они переходят на нормальные вычисления.
раскрыть ветку (16)
У нас в школе при умножении с самого начала были два множителя и произведение, равно как и при сложении - два слагаемых и сумма
И так же с самого начала рассказывали, что от перемены мест результат не меняется
раскрыть ветку (1)
Раньше учитель мог объяснять как хочет, сейчас наплодили этих методичек и требует их соблюдения. В теории, при таком подходе нет ничего плохого, но тут уже все зависит исключительно от умения учителя доносить информацию. И учебника, который в теории должен это все объяснять в т.ч. родителям тоже.
Может, что-то сильно поменялось, у меня начальная школа была в девяностых, потом мехмат, но слово "множимое" я вижу впервые в жизни. Всегда было два множителя, как два слагаемых. По-разному элементы назывались лишь в асимметричных операциях вроде вычитания или деления.
раскрыть ветку (1)
Да, у меня такого тоже не было, пока я учился. Хотя Большая Советская Энциклопедия содержит именно такое определение умножения и разделение на множимое и множитель. Сейчас это вроде как является педагогической практикой, решать именно так, пока не дойдут до перемены мест множителей. А дальше нормальная математика в понимании взрослого человека и алгебры. Это уже тут всплывало несколько лет назад: https://pikabu.ru/story/iz_metodichki_dlya_uchiteley_obuchen...
А нам в самом первом классе про перемену мест слагаемых и множителей рассказывали. Даже помню иллюстрацию где две руки держат цветы или игрушки какие-то и руки сначала нормально держат, а потом скрещивают.
В моё время, когда допускали эту "ошибку", то учитель не снимала балл, а стрелочками указывала, что надо числа было множить в другом порядке и ставила минус. И когда делали работу над ошибками, она как раз объясняла, что "умножаем 4 ручки на количество пеналов".
Определение a * b = a + a + a ... + a (b раз) ничем не отличается от определения a * b = b + b + b ... + b (a раз). Поэтому не имеет значения, каким определением пользуется школьник.
раскрыть ветку (7)
Профессор математики огрел бы вас стулом за такую ересь, просто потому, что определение есть и оно одно. Причем дано этими самыми профессорами математики и не только в России.
ещё комментарии
На самом деле математики, например, Вербицкий, считают, что "таких учителей надо дико бить палками, а потом увольнять с волчьим билетом. Потому что это не учители, а говно натуральное, выродки тупые вообще" - http://lj.rossia.org/users/tiphareth/1685303.html
А школьник дал другое определение, и теперь их два. То, что вы считаете, что одно определение лучше другого, когда они равноправны, как раз и говорит о том, что от математики вы далеки.
раскрыть ветку (5)
А школьник дал другое определение, и теперь их два.
Мне больше нечего сказать, вы уже все сказали за себя.
раскрыть ветку (4)
Идея, будто справедливость математических выводов зависит от того, школьник или профессор их сделал, а не от того, насколько хорошо они обоснованы, также чужда математикам.
Но, вообще-то, хватит прикидываться, будто математики на стороне учителя, я уже привёл слова Миши Вербицкого.
раскрыть ветку (3)
Какое мне дело до одного Миши, если есть международные организации ученых? И они дают определенные стандарты, определения и выполняют работу на международном уровне.
Во-вторых, учитель тут причем? Если вы не в курсе (а вы явно не в курсе), то у учителя есть методические указание и потом приходит проверка и дрючит его за их невыполнение. Достаточно одной тетрадки без исправления подобной "ошибки" и понеслась. Это разве проблема учителя? И люди, которые настроены против учителя, просто недалекие в этом плане. А лапки проблемы растут из минобра, в котором сидят не математики, а чиновники и они определяют стандарты образования. Математик способен пояснить данные операции корректно через определение, у минобра это сделано через задницу.
раскрыть ветку (2)
Один Миша - это на одного реального математика больше, чем приведённый вами профессор, который огрел бы меня стулом.
Математики не очень парятся над соблюдением единообразия формальных договорённостей. Кто-то включает ноль в натуральные числа, кто-то не включает, и всем норм.
Я не проверял, но предполагаю, что значение порядка множителей - это изобретение плохих педагогических колледжей, а не указания Министерства образования.
раскрыть ветку (1)
Я не проверял, но предполагаю, что значение порядка множителей - это изобретение плохих педагогических колледжей, а не указания Министерства образования.
А возможно и то и другое, иначе не знаю, как такое могло придти в школы. Шесть лет назад уже был срач по этому поводу: https://pikabu.ru/story/iz_metodichki_dlya_uchiteley_obuchen... Я просто рассказал, почему так решают и на каких определениях строится обоснование решения в арифметике для 2 класса по методичкам, длится эта вакханалия до изучения переместительного закона (не очень долго). И во взрослом мире все по другому, тут я с вами согласен.
ещё комментарии
Походу это мнение отдельно взятого опёздола с дипломом педагогической шараги. Потому что очень многим было на это насрать.
раскрыть ветку (1)
Идея хорошая, реализация говно.
Особенно страдают дети, которые ко второму классу уже знают переместительный закон и не могут понять, почему им решения перечеркивают. А учитель не может ему объяснить, почему надо "именно так" из-за неправильно поставленной задачи.
ещё комментарии
Что за дичь? В "правильном" решении у вас 4 ручки взять 3 раза, а в "неправильном" появляются пеналы (вместо раз) и выглядит как явный бред, атата, учитель прав. Заменили слова неуместно и выставили решение бредовым. А на самом деле речь только о том, 4 ручки взять 3 раза или 3 раза взять 4 ручки. И они абсолютно одинаковы
раскрыть ветку (16)
классическая подмена понятий только чтобы его вариант выглядел (не являлся, а лишь выглядел в глазах большинства) единственно верным. подсказать кто кроме учителей этим занимается у нас в стране?
ещё комментарии
ещё комментарий
Потому, что согласно определению умножения в арифметике, на первом месте стоит множимое, а на втором множитель. Поэтому читается оно всегда в таком порядке: a * b = взять "a" предметов "b" раз. Свойство перестановки тоже читается по другому a * b = b * a (взять 4 ручки 3 раза = взять 3 ручки 4 раза), но второклассники проходят его позже, а потом идут абстрактные вычисления и все это уходит в привычную нам алгебру.
раскрыть ветку (12)
раскрыть ветку (6)
Откройте любой современный учебник для 2 класса одобренный министерством образования. Скорее всего, вы увидите там именно такое определение или вкладываемый смысл. У меня же нет под рукой библиотеки для младших классов, каких-либо проверенных сайтов, а у взрослых все по другому и никто этим не заморачивается т.к. нет размерностей из-за абстракции. Мое дело пояснить было, а не убедить в единственной правильности этого подхода.
раскрыть ветку (2)
Ну вы это вообще молодец - подтверждать верность подходов описанных в учебнике, определениями из этого же учебника.
раскрыть ветку (1)
Я не подтверждаю верность этих подходов, я подтверждаю их используемость во втором классе и что такое существует. Заметьте, после второго класса их уже никто не использует и все возвращается к нормальной математике. А кто утвердил их использование для второклассников и посчитал их верными, это уже не ко мне, а к тем, кто одобряет подобные учебники и методику обучения.
Кстати это определение содержится в большой советской энциклопедии: https://gufo.me/dict/bse/Умножение
раскрыть ветку (2)
Только сейчас заметил подлог. Взять 4 ручки (a) 3 раза(b) = 3 раза(b) взять 4 ручки(a), то есть a*b=b*a. В вашем же случае получается, что вы меняете местами смыслы, то бишь значения, а и б во второй части.
раскрыть ветку (4)
В алгебре нет размерностей и соответственно правила "а предметов b раз", там чистая абстракция без размерностей. Данное правило действует только для второго класса, пока не вышли в перемену мест множителей. При этом им могут объяснять это на реальных предметах так: есть плитка шоколада из 12 подушечек, разрезать ее можно на 4 части по 3 подушечки (3 подушечки взять 4 раза) или на 3 части по 4 подушечки (4 подушечки взять 3 раза). Я подсмотрел, как это делается, поэтому подлог совершен не специально. Когда дети это усвоят, уже все равно, что на что умножать и дальше идет нормальная математика.
раскрыть ветку (3)
Это все понятно как раз. Непонятно одно- где вы нашли ограничение для второго класса и почему учителя считают ошибкой правильный ответ?
раскрыть ветку (2)
Не первый раз вижу подобное, причем не только в виде жалоб родителей. Когда интересовался, откуда это, то и методические указания всякие встречал в интернете. Один из примеров на пикабу, но далеко не единственный:
https://pikabu.ru/story/iz_metodichki_dlya_uchiteley_obuchen...
раскрыть ветку (1)
Постоянно в школе бесило это дописывание чего ты считаешь. Полная дичь. Еще и ебали мозг потому что не допишешь, что тут 5 гвоздей, а тут 3 яблока.
"сложить X предметов Y раз"
а может Y раз сложить по X предметов?
это блять не английский язык с железными правилами построения фраз - у нас оба варианты удовлетворяют допустимы.
ещё комментарии
Любая наука и особенно математика очень строгая, посмотрите определение умножения: a * b = a + a + a ... + a, (b раз). Поэтому мы берем X (множимое) предметов Y (множитель) раз и никак иначе. Операция перестановки тоже строгая: взять X предметов Y раз = взять Y предметов X раз, где предмет один и тот же.
раскрыть ветку (9)
посмотрите определение умножения
a * b = b * a
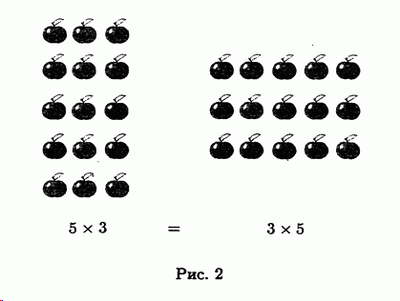
Учитывая уровень интеллекта, который вы деконстрируете... Посмотрите на картинку. Подумайте. Потом, если вам что-то еще будет непонятно, задавайте вопросы.
раскрыть ветку (1)
Да, у меня есть пару вопросов:
1. Зачем вы скидывает картинку, которую я уже скидывал? И которую я описывал ещё в другом месте на примере плитки шоколада? И которую второклассник ещё не знает?
2. Зачем вы что-то пишите об интеллекте, если сами не осиливает посмотреть пару соседних комментариев и разобраться в написанном, но зато упорно лезете с глупым утверждением?
Извините, но мне лень писать объяснение двадцать раз подряд, учитывая что у остальных проблем с пониманием не было. И я сейчас не говорю о тех, кто со мной согласен, а как раз наоборот считают данный подход в обучении(!) бредом и продолжают так считать.
Поэтому мы берем X (множимое) предметов Y (множитель)
и где тут указание на то, что тут обязательно первое, а что обязательно второе?
на английском это все например: "B times A", т.е. ровно противоположно тому, что ты пытаешься навязывать, заявляя о точности математики.
это момент - не математика, а традиция, хотя на самом деле долбоебизм.
раскрыть ветку (6)
От того, что вы взяли английский аналог, суть от этого не поменялась. Вы все равно не имеете права записывать числа по другому, если дано четкое и конкретное определение: `adding 3 copies of 4 together` - 3 раза 4. Добавьте размерность и ничего не изменилось, просто теперь записываете наоборот и учитель перечеркнет другой вариант 4 * 3 = 3 * 3 * 3 * 3 (все еще складываем пеналы, англ. вариант определения).
раскрыть ветку (5)
ты хоть сам понимаешь, что твои аргументы это: "оно так просто потому, что оно так, а не иначе"?
раскрыть ветку (4)
Мои аргументы сводятся к стандартизированному и общепринятому варианту определения. Определения в мире науки, это закон. А ваши сводятся к выводам, которые делаются на его основе, которые вы используете интуитивно. В третьем классе как раз выводы объясняются и все становится на свои места. Поэтому проблемы не в самом методе, а в том, как это организованно для второклассников.
раскрыть ветку (3)
закон в мире науки это: "от перемены слагаемых результат не меняется".
это математика.
а это "4*5 - правильно, а 5*4 неправильно" - к математике никакого отношения не имеет и равнозначно запоминанию и выучиванию бесполезных правил, не имеющих никакого отношению и к реальному миру, и к миру математики.
ещё комментарии
раскрыть ветку (1)
Множители, какая разница?
Вот при делении и вычитании - да, место имеет значение. А при сложении и умножении место значения не имеет, ибо в условиях задачи есть пояснение и уточнение, что собой являет та или иная цифра/число.
ещё комментарии
ещё комментарии
Товарищ, вводя размерность, нужно хотя бы чуточку понимать что это. У вас 4 ручки на пенал. А не просто 4 ручки. Километры в час помните? Так вот тут тоже самое. 4 ручки/пенал * 3 пенала = 12 ручек. 3 пенала * на 4 ручки/пенал = 12 ручек. Умножение коммутативно. 3*4=4*3.
С приветом, дипломированный математик.
С приветом, дипломированный математик.
раскрыть ветку (1)
Когда пишите комментарий, удостоверьтесь, что он не написан и не обсужден уже раз двадцать в соседних ветках в паре сантиметрах от ваших глаз. Это касается как размерностей, так и коммутативности, так и их применительности для второклассников. А то это показывает недалекость ума, даже не смотря на его "дипломированность".
раскрыть ветку (4)
Математическое определение умножения a * b - взять a предметов b раз: a * b = a + a + a ... + a, (b раз). Свойства перестановки тоже по другому объясняются, пеналов вы там не увидите: 4 ручки по 3 раза = 3 ручки по 4 раза. Поэтому мы получим и там и там ручки, даже если поменяем местами множители. Но пока операция перестановки не проходилась, соблюдается строгий формализм. Операция перестановки так же хорошо показана в википедии (на удивление):
Потому что пинал и ручки не математические величины, умножаем количество одних на количество других.
раскрыть ветку (2)
ещё комментарии
ещё комментарий
А почему бы не взять 3 раза по 4 ручки или 5 раз по 2 шарика, если уж так принципиально иметь "множимое"? (У нас в советской школе и слова такого не было, было множитель и множитель)
раскрыть ветку (1)
Учитывая опыт предыдущих ответов и вопросов к ним, скажу так: во втором классе сначало действует урезанное правило а * b - "взять а предметов b раз". Принципиальным это считается недолго, до того момента, пока детям не расскажут правило перестановки и это правило больше не применяют, выходя в нормальную математику. У меня тоже в школе такого не было, но кто-то решил ввести это в педагогическую практику, я же просто пояснил логику для родителей.
А то,что в выражениях коэффициент пишется перед переменной, разве не выглядит логичным? 3*х например. Я бы написала 3*4 в таком случае. Но в рамках конкретной задачи не вижу разницы в порядке записи.
раскрыть ветку (1)
На первом месте множимое, потом множитель. В любом случае после изучения перестановки можно этим не заморачиваться и ставить как хочется. Взрослые как правило даже не думают, что под этим есть формальное доказательство и логика - главное работает и ладно.
Учителя не могут объяснить детям, что такое размерность и как следствие учат хуйне. То, что вы написали - идиотизм с кучей логических ошибок, про которые ниже написали.
Как думают учителя: 3 пинала * 4 карандаша = 12 пиналокарандошов. Видят, что выглядит не очень и поэтому говорят - что финальную размерность определяет та размерность, которая идет раньше, а второю - отбрасывают.
Как надо оформлять такой пример, чтобы к нему не доебались:
3 пинала * 4 карандаша/пинал = 12 карандашей.
Над размерностью производят те же операции, что и над самими значениями.
В действительности, все объяснения умножения через сложения справедливы только для безразмерных натуральных чисел.
Я бы посмотрел как учитель будет объяснять таким образом что-то такое:
15,5(км/ч) * 185 (мин).
раскрыть ветку (6)
Согласен.
Единственное они не могут написать размерность карандаша/пинал т.к. деление и сокращение дробей к этому моменту не пройдено. Поэтому поясняют как могут, потом тут же давая правило перестановки и выходя на нормальное умножение.
раскрыть ветку (5)
Поправить программу и давать все последовательно, объяснить детям как работают размерности? да не бред какой-то, лучше будем врать и учить их тому, что противоречит законам математики. 10из10
раскрыть ветку (4)
Я бы посмотрел, как вы бы им это объясняли) Проще вообще работать без размерностей, чем потом копаться в болоте таких размерностей.
P.S. На данный момент ничего законам математики не противоречит, а используются допущения и упрощения, которые потом расширяются до нормальных рамок. Вас же устраивает, что учитель в начальных классах без объяснений зачеркивает вычитание из меньшего числа большего т.к. ребенок еще не знает отрицательных чисел. Или говорит, что корня из отрицательного числа не существует, а потом ему суют комплексные числа.
раскрыть ветку (3)
Нет, меня не устраивает. Я объяснял детям и не такое.
Правильно, кому-то проще, и пофиг на детей.
Противоречие в том, что запрещена коммутативная операция.
раскрыть ветку (2)
Моей целью было донести до родителей, что во втором классе действует правило а * b - "взять а предметов b раз", которое потом экстраполируется в нормальную алгебру. Возможно, это поможет им преодолеть трудности, которые возникают из-за непонимания логики учителей. Настаивать на правильности этого подхода в обучении я не собираюсь, поэтому ничего не имею против ваших рассуждений.
раскрыть ветку (1)
Я вас понял. И с вами согласен, но делали вы совершенно иное. В вашем объяснении не упомянуты те самые упущения из-за которых весь кипиш и фактически оно неверное. Когда ошибки были выявлены, вы сказали, что малышам они будут непонятны, но при этом само объяснение было рассчитано на родителей.
Если вы преследовали эту цель, то вам надо было изложить все теорию со всеми допущениями и ошибками. А решение уже бы принимали родители. Да и логика учителя здесь не причем, а только его лень, либо отсутствие квалификации.
Не надо воспринимать такие вещи как норму, иначе нам всем будет жопа.
Ну да - подловил учителя в тёмном переулке, отпиздил его , напевая под нос "каждому лектору в жопу по вектору" и проходит такой недуг у проводника к знаниям.
раскрыть ветку (1)
да нет, ваши дети тоже так учились. и вы так учились - это всегда требовалось в арифметике. Мы узнаем. сколько было карандашей? значит, карандаши умножаем на коробки, не наоборот. Ну такое правило. Учитель должен требовать это от учеников.
Задание номер 4 вроде не полностью сделано (там в см и мм надо было измерить), но там +. А за правильный математический пример +-. Где там логика?
По мне, так 5 * 2 как раз по тексту задания, т.к. У 5 ребят по 2 шарика = 5 самцов
Потому как 2 * 5 это, По 2 шарика у 5 ребят
раскрыть ветку (28)
5*2=5+5
2*5=2+2+2+2+2
Детей учат не только умножать, но и понимать, что они умножают и зачем.
Это когда вы считаете ребят с яблоками - в общем-то пофиг, что на что умножать. А когда вы начнете считать, сколько вариантов у пяти детей выбрать по пять яблок из пяти сортов, расположенных определенным образом в 5 корзинах...
раскрыть ветку (27)
Но ведь у 5 ребят по 2 шарика, т.е. 5*2=2+2+2+2+2. Разницы никакой. Чисто субъективное восприятие человека. Не стоит оправдывать этот идиотизм.
ещё комментарии
раскрыть ветку (14)
Кто это решил? Это все ещё 5 ребят и 2 шарика у каждого. Просто один "умник" решил что такое написание будет значить "два раза по пять", а не "пять раз по два", хотя последнее даже звучит логичнее. Вы ведете себя как радикалы какие-то. Любое инакомыслие пресекается на корню, вместо того, чтобы объяснить что это одно из верных решений. Жаль что у нас в школах есть такие люди.
раскрыть ветку (8)
Все верно, по скольку у каждого было по два шарика, а ребят было пять, то что мне мешает 2х5. Это и называется логика. Ребенок ведь в ответе написал 2+2+2+2+2=10, где ошибка?
Собственно, примерно это я и хотел сказать.
А так у многих возможно и появляется машинальное желание написать 5 * 2 из-за построения текста задания. Конечно, задание вида "У каждого мальчика по 2 шарика. Мальчиков 5. Сколько у них шариков?" Выглядит корявее, но явно располагает необходимые акценты и больше захочется написать 2 * 5 уже.
Вот если бы при этом всём привели конкретную формулу вида:
предмет(или его количество) * сколько раз = общее число предмета
то многие не спорили, т.к. многие не знают конкретные требования, а как кому-то кажется что есть только один вариант записи - это бред. Как условишься, так и будет. Так-то всё вокруг нас состоит из условностей, и речь и прочее, но это не говорит о том что так делают все. Не все пишут же буквы одним и тем же способом.
Возможно, некоторые дети понимают суть, но восприятие "раз * что-то", для них лучше чем "что-то * раз". И менять это, как левшу правой рукой заставлять писать - будет каждый раз дёргаться сначала левой рукой, потом внутренне ломать свой естественный уклад и через силу заставлять делать это медленно, коряво, получая стресс. В данном случае надо донести суть на уроке, а задания или соответствующие главы с заданиями должны содержать конкретные требования. При этом, лучше делать пометку, что необходима конкретная запись(ссылка на главу), чтоб у ребёнка, который мыслит иначе не возникало каши от того, какой вариант надо, т.к. для него правилен один вариант, но он начнёт сомневаться что ошибся, как результат - получит худшее восприятие темы и багажом ещё начнёт развивать в себе неуверенность. В лучшем случае такого ребёнка достанет нападки, что он всё делает не так, и он начнёт ни во что не ставить чужое мнение и плевать на него, в худшем - получим тупящщего, тормозящего и неуверенного и замкнутого в себе.
Кто это решил?
Скорее всего греки. Множитель это то, что стоит вторым. Множимое - ставится первым. По определению. Всем похуй что ты считаешь иначе. Иди создавай свою математику, со своими правилами и доказывай что она лучше нынешней.
@MarisaChan ну и тебе тоже заодно.
раскрыть ветку (5)
множимое? што?
ок, допустим это не бред героинового наркомана.
в двух вагонах поезда едут по пять мальчиков, каждый из которых держит по 2 шарика. сколько шариков едет в подвижном составе?
ну ка, давай ка расскажи мне, как называется число, которое стоит третьим?
а если ещё чисел в умножении добавить?
раскрыть ветку (2)
Ну тоже логика не самая. Действия производятся по порядку. Соответственно, участвуют одновременно лишь два члена уравнения. С остальным согласен.
Мдаа, человек не способный уловить такую простую мысль высирает аргументы на уровне "шах и мат атеисты".
Там нет третьего числа, ибо ты не перемножаешь три значения одновременно. Ты в любом случае умножаешь только два. Например находя общее количество мальчиков, а затем выполняя действие по шарикам.
а вот ещё тебе задачка.
сила, изменяющая за 1 секунду скорость тела массой 1 кг на 1 м/с в направлении действия силы давит на один квадратный метр поверхности.
сколько паскаль давление?
что у нас тут по твоему определению множимое, а что множитель, и как называются остальные величины, раз у тебя названия есть только для двух.
Свою математику?) Вы пишете ерунду, одно из основных и элементарных правил математики: "От перемены мест множителей произведение не меняется". Это не я придумал. А вот ту чушь, которую вы защищаете, придумали точно не греки.
Какая такая логика так говорит? Сложение должно в голове происходить у ребенка на начальных этапах. 5*2 или 2*5 не важно, он просто представляет себе 5 детей с 2 шариками у каждого и все. Запись не должна играть роли в данном случае.
раскрыть ветку (4)
Школьная логика говорит о том, что первое число в таких выражениях идет то, что берем, а второе то, сколько раз берем первое. При этом ребенок может прекрасно осознавать что и как, но критически мыслить программа обучения не дает, однако критически мыслит не много ребят, так что идти поперек правил зачастую бессмысленно, все зависит от конкретных ситуаций. Как сам помню, были преподаватели, которые позволяли отходить от правил в расчетах. Зная, что ученик прекрасно понимает то, что считает.
раскрыть ветку (3)
Что за бред? Какая разница 5 раз берем 2 шарика или 2 шарика берем 5 раз? Кольцо целых чисел коммутативно по умножению, какая разница-то? Некоммутативные кольца вообще в школе, емнип, не проходят!
раскрыть ветку (1)
Ну и что кто берет?
5 мальчиков, 2 шарика.
Берем 2 шарика по 5 раз, или у 5 мальчиков по 2 шарика ?
Мы сами выбираем множитель. Либо количество пацанов, либо количество шаров у каждого поцана.
ещё комментарии
Ты явно не прав и в школе учился плохо, потому что на самом деле вот так:
5*2 = 2+2+2+2+2
2*5 = 5+5
А то, что ты написал это ересь и вообще не по канону. И поэтому тебя нужно сжечь, даже если ты красивый.
раскрыть ветку (9)
Как раз не правы вы.
Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемое столько раз, сколько указывает множитель.
раскрыть ветку (3)
Я утверждаю, что множитель в данной записи стоит первым, что даже нашло отражение в особенностях и стилистике русской речи: "пять раз по два".
Я подожду ваших опровержений, хотя и утверждать обратное есть попрание всех основ, форменное издевательство и вообще!
раскрыть ветку (1)
Мы сами выбираем множитель. Либо количество пацанов, либо количество шаров у каждого поцана.
ещё комментарии
Вы не правы. На правах кандидата технических наук заявляю, что a*b - это b раз просуммированное a.
раскрыть ветку (4)
ещё комментарии
реально дичь какуюто несешь, ответь, почему 5*2 произносят как "пятью два"? потому что пять раз по два... таблицу умножения помнишь как учил?
ещё комментарии
раскрыть ветку (2)
Бред. Математика это инструмент для получения результата и не имеет значения к какому в прикладном плане этот результат имеет отношение. Тот кто решает задачу используя математические действия изначально понимает к чему полученный результат имеет отношение. По этому для решения любых задач математическими инструментами не имеет значения к каком понятию привязано то или иное число. Значение имеет только результат. Все остальное-чушь. 5 вилок в 3 коробах. Сколько всего вилок? Ответ вы получите в вилках, независимо от того как вы оформите решение задачи.
Интерсно какой дегенерат это написал?) Это как минимум математически неправильно, т.к. мы исключаем коммутативность операции умножения.
Очень сильно бомбил от этого. Жена сказала не бомбить, а дочке сказала, просто ставь вперед то, что ищешь. Но вот прошло полгода, я заметил, что училка уже хуй кладет на то, какое число впереди. А в начале года прям пиздец был.
раскрыть ветку (1)
а отрезок в миллиметрах ни учитель, ни ученики посчитать так и не смогли? т.к исправлений нет
Я конечно с вами согласен... Но думаю, вопрос был сколько всего шариков, в итоге нужно 2 шарика умножить на 5 ребят. А учитель посчитал что 5 ребят умноженное на количество шариков это не правильно.
Ну в хрень какая то все равно
Ну в хрень какая то все равно
раскрыть ветку (4)
Ваша проблема в том, что вы ШАРИКИ умножаете на РЕБЯТ, а умножать нужно КОЛИЧЕСТВО шариков на то КОЛИЧЕСТВО раз, сколько их нужно взять.
И тогда никаких проблем взять пять раз по два шарика или по два шарика взять пять раз.
Если у той училки в голове тоже шарики на ребят умножаются, то у нее проблемы с головой и ее точно из школы гнать надо.
раскрыть ветку (2)
Тоже подумал сначала гнать, но теперь я хоть ее логику уловил. Может быть это проф деформация, поскольку как раз дети могут не понимать почему одно на другое умножается.
Дочка вчера тоже четверку принесла. В учебнике написано 600х350, а ребенок умножил 350 на 600. Умножение в столбик, у учителя видимо шаблон не сошелся.
раскрыть ветку (3)
Причём подобный вариант даже проще при умножении руками, ребёнка похвалить только за оптимизацию.
раскрыть ветку (2)
Тут на днях с ребенком степь рисовали, нарисовали юрту, лошадок травку зелёную, двойку принесла. А ведь всей семьей сидели , думали , как бы по красивше сделать. Даже подписали - Калмыкия ( Мы Мурманчане ) Предмет, "Окружающий мир" Учитель сказал, что степь должна быть желтая. И ниипет!))
Думаю, логика тут в том, что первым должно идти кол-во шариков, т.к. вычислить надо именно их. В заглавном посте то же самое - раз надо узнать, сколько ручек, исходное количество ручек ставится на первую позицию. Для взрослого, конечно, бред, но мы уже умеем умножать, а ребенок только учит сам принцип.
раскрыть ветку (1)
Учился в школе с 1993 по 2003 и нас точно так же заставляли располагать множители, так что это не какой-то новый тренд )
раскрыть ветку (1)
Пффф! 93-2003...
Это "правило" было сформулировано ещё в советском методическом пособии для обучения начальных классов лет 60 назад. К сожалению, не могу вспомнить автора, встречал пару лет назад в сети.
Я тут кстати сильно думал над этим и вспомнил. В первом классе у нас требовали, чтобы вот в таких вот примерах первым множителем был тот, который будет стоять после равно. Т.е. если считаешь шарики а коробках, то шарики*коробки=шарики. И тоже пару раз ловил минусы за это, благо во втором классе я перешел в другую школу. И там была такая же херня, так как ебучий Петерсон
раскрыть ветку (1)
и самое интересное, что это правило вырабатывают, а потом на него хуй кладут к классам повыше. и поступив в вуз, кладите хуй на школу.
а на работе - вообще кладите хуй на все (у нас тут свои правила) = замечательная система.
Там просто учится табличка на 2. Должны были разные что подчеркнуть и на уроке объяснить, что не надо спешить и надо пока разобраться с табличкой на 2. Или если и перечеркивать, то не отнимать балл.
раскрыть ветку (1)
Скорее дополнительно побеседовать с ребёнком, чтоб удостовериться, что он понял суть данного действа. Пусть сам проговорит свои записи.
Так в школе же обучали этому. То, что считаем - должно быть на первом месте. Количество на втором. То есть например нам надо посчитать, шарики у ребят: шарикиуодного*количестворебят=шарикиувсех
раскрыть ветку (1)
а когда смету в строительстве считаешь, все наоборот, сначало количество того что считаем, а потом сколько за штуку... сам удивился когда столкнулся, но оказывается все просто, так проще спецификации из проекта в сметы в екселе переводить
Ну здесь то хоть понятно. Вторым способом расписали как 2*5. При первом примере надо было 5+5=10.
раскрыть ветку (2)
Пять ребят по два шарика, где вы 5+5 нарыли? Видать вы такой же учитель как в примере )) Ну разве что пять шариков в левой руке плюс 5 шариков в правой руке, но это вообще уже за гранью понимания...
раскрыть ветку (1)
Первая переменная - ребяты с шариками, их 5, затем считаем, сколько шариков у каждого, их 2, соответственно слагаемых пятерок будет так же 2. Можно сделать и 2+2+2+2+2 и 5+5. Разницы в результате нет, есть разница в логике, которая помогла придти к результату, но оба варианта верные.
Взяли 2 шарика 5 раз, не 5 шариков 2 раза... Это в примерах по фиг перестановка мест множителей, а в задачах строго... Взять что то столько то раз... Это как мне учительница начальных обьяснила
раскрыть ветку (1)
а почему нельзя взять 5 человек по 2 шарика?)
или 2 шарика по 5 человек ( второе даже звучит убого )
Потому что сейчас они должны понять логику умножения, а не просто заучить табличку. 2*5 - это два взять пять раз. Да, оно равно 5*2, но смысл теряется. Точно так же, если бы он в первом примере написал 3*8=24, это было бы неправильно с точки зрения логики преобразования сложения в умножение. Не 3 сложенное 8 раз, но 8 - трижды
Тут знакомой, похоже, надо к директору, а если тот не поможет, то в РОНО обращаться, пидорская, блять, училка, у меня в свое время любовь к географии одна падла отбила...
раскрыть ветку (1)
На порядок умножения обращают внимание именно в начальной школе, когда изучают принцип умножения. Понять принцип или тупо заучить, ничего не понимая - это совершенно разные вещи. Взрослые из-за того, что уже забыли такие мелочи из начальной школы и могут не задумываясь, на автомате умножать, делить недоумевают " а какая разница?" и детям говорят "вот училка не правильно вас учит". А учительница учит по методике, которая не менялась с советских времён.
раскрыть ветку (18)
учительница учит по методике, которая не менялась с советских времён.
Когда сразу учили:
"От перемены мест слагаемых сумма не меняется."
И
"От перемены мест множителей произведение не меняется."
И таким бредом как сейчас не занимались.
"От перестановки мест множителей произведение не меняется"©
"От перестановки мест слагаемых сумма не меняется"©
Вот это - методика советских времен. До сих пор от зубов отскакивает.
А то что вы пишите - херня из под коня, а не "советская методика".
ещё комментарии
при чем тут перестановка? Учат понимать смысл написанного, а не тупое знание. Знаешь чем отличает ум от интеллекта? В том, что ты не просто знаешь, что 5х2 = 2х5, а в том, что ты знаешь чем отличается 5 по 2 и 2 по 5
раскрыть ветку (9)
ещё комментарии
Дело не только в математике, тебя учат правильно воспринимать информацию, описанную в задаче, а не оперировать только абстрактными числами
раскрыть ветку (2)
Дело в математике. И её учат именно для того чтобы понимать что "3 пенала по 4 ручки" и "4 пенала по 3 ручки" - это одно и тоже количество ручек.
Чтобы потом в магазине не думать что 4 пачки %продукта% по 250 грамм это лучше чем 2 по 500.
Ну и? 5 ребят имеют по 2 шарика или по 2 шарика у 5 ребят. Хоть как меняй местами и умножай, сути не меняет.
Для примера из поста:
3 пенала умножить на 4 = 12 пеналов
4 ручки умножить 3 = 12 ручек
Смысл поменялся, не правда ли?
раскрыть ветку (4)
Я бы ща доколупался что вы "для примера" одну единицу измерения выбросили а другую оставили.
Но вам потом на физике в 6-м классе за это по голове дадут.
а если немного подключить мозги, то получим следующее:
3 пенала умножить на 4 ручки = 12 ручек
4 ручки умножить на 3 пенала = 12 ручек.
ещё комментарии
ещё комментарии
Определение. Умножение — это действие в результате которого находят сумму одинаковых слагаемых. Умножить число а на число Ь означает найти сумму Ь слагаемых, каждое из которых равно а.
но какой от этого смысл, если.
Переместительный закон
Правило. От перестановки множителей произведение не изменяется.
Я ещё понимаю, если были задачи посложнее, где были бы выявлены существенные ошибки в ответе при не правильном применении умножения\деления.
Но цель найти количество ручек, хоть как умножай ответ будет один, ведь при умножении количества пеналов с ручками на количество ручек в этих пеналах мы не получаем пеналы, мы получаем ручки.
к сожалению, но большинство, "взрослых" комментаторов на пикабу этого не понимает, так как каждый считает себя "умным", а потом дети получают полтора землекопа!
раскрыть ветку (2)
вы бы хоть пояснили какое отношение ваши «полтора землекопа» имеют к порядку записи коммутативных операций?
Если вы решите апеллировать к единицам измерения, то будете неправы ибо умножаются единицы вида чел. * шарики/чел.
Какая разница как считать, если ты под ответ полтора подвел землекопов, которые всегда натуральные? Почему бы просто не сказать писать 1.5(ям). И правила соблюдаешь и голову включаешь.
Вроде бы эти методики каждый год обновляются, не? По одной и той же методике у нас только преподаватели-пенсионеры учат...
раскрыть ветку (1)
ещё комментарии
ещё комментарии
Логично что от перестановки сумма не меняется- это мы уже давно поняли. Тут есть такая тонкость что отталкиваться нужно от шариков и мы видим что логичней и примитивней сумму прописать как 2+2+2+2+2=10(2*5, два шарика плюс два шарика и т.д.), писать сумму как 5+5=10(5*2) вообще не логично в данной задаче для школьника(пять ребят плюс пять ребят, а шары где?))) ) . Повторюсь, от перестановки сумма не меняется, но логику умножения правильна в ответе 2*5 если отталкиваться от суммы.
раскрыть ветку (5)
Тут логика в другом. Вы сможете доказать что а*b=b*a? Боюсь что не сразу, потому и умножать нужно так как научили. Как только вы сможете учителю доказать коммутативность умножения - умножайте как хотите.
раскрыть ветку (4)
Коммутативность операций сложения и умножения это аксиомы арифметики. Умножение по определению коммутативно, это не нужно доказывать. Раньше в школе изначально этому учили, от перемены мест слагаемых сумма не меняется, то же самое и для умножения. Как раз на данном конкретном примере это можно было бы отлично показать. Да, по определению 5*2=5+5, 2*5=2+2+2+2+2, но так как от перемены мест множителей произведение не меняется, то вы можете писать в любом порядке и это будет правильно. Перечеркивание ответа и снижение оценки вызывает больше вопросов и негатива, а пользы никакой не несет.
раскрыть ветку (3)
Извините конечно, но ваши познания в математике на уровне Занусси, с их шедевральным "параллельные прямые не пересекаются. Доказано Евклидом".
Что бы не быть голословным, пример когда умножение некоммутативно - матрицы.
раскрыть ветку (2)
В арифметике умножение коммутативно, это аксиома. В евклидовой геометрии параллельные прямые не пересекаются, следствие пятой аксиомы.
Я вашу точку зрения понял, дальше нет смысла спорить.
раскрыть ветку (1)
Параллельные прямые не пересекаются - это постулат, предположение. На этом предположении основывается евклидова геометрия. Неевклидова, например Лобачевского, обходится без этого постулата.
Постулат != Аксиома.
Выше привёл вам пример, арифметика матриц, где умножение некоммутативно.
почему они зачеркивают? что, там у 2 шариков по 5 ребят? как они это объясняют детям? и не действует ли правило от перемены мест ?
Чето я нихуя не понял. Первым же идет число пять, поэтому правильно 5 на 2. Или нужно было еси 5*2 пишешь, то писать потом 5+5?
Я не согласен с учителем. В задаче Ф3 сказано в такой последовательности: у 5 ребят по 2 воздушных шарика. Значит и решение в автоматически пишется соответственно 5*2.
Тут что-то типо если спрашивают сколько шариков, то нужно сначала шарики брать и умножать на число. Зачем это не совсем понятно, может как-то заранее готовят к единицам измерения
Когда я училась в школе, нам учитель объясняла, что нужно умножать предмет на количество человек, если нужно узнать кол-во предметов, если наоборот, то это будет кол-во человеков. Если бы это был пример, а не задача, то перемена мест слагаемых роли бы не играла
Я разгадал ее логику: во всех примерах выше первым идёт то число, которое повторяется при записи сложения (3+3+3+3+3 -> 3*5). В примере три несколько раз повторяется двойка (2 шарика пять раз), поэтому 2*5. С точки зрения математики ставить ошибку здесь бред, но логика кажется такая. Может им дали конкретный алгоритм решения задачи и теперь проверяют знание алгоритма, а не ответ?
всё верно, первым идёт то, что нужно посчитать. с ложении перестановка слагаемых возможно тк подразумевается объединение двух однотипных слагаемых. в то время, как в умножении разнотипные. потом в ответе и пишут "10 шариков", а не просто 10
С нельзя с этим решением к учителю подойти и уточнить, в чем прикол и за что снизили?
Послушать аргументы.
А-то как обычно двояко. Вроде и бред снижать за это.
С др стороны, смотря как проходят по программе.
Наша учитель была лояльна и закрывала глаза на такое. Но это было лет 20 назад уже.
Послушать аргументы.
А-то как обычно двояко. Вроде и бред снижать за это.
С др стороны, смотря как проходят по программе.
Наша учитель была лояльна и закрывала глаза на такое. Но это было лет 20 назад уже.
А если бы он написал 5·2=10; 5+5=10, что бы поставили? У пяти ребят есть по одному шарику и ещё по одному шарику — всего 10. Судя по предыдущему, порядок сомножителей такой же как в фразе "слагаемое x повторяется y раз" = x·y
Уже много таких примеров было. И учитель здесь прав. Это определение действия умножения и на данном этапе порядок произведения важен. То есть 2+2+2+2+2=2*5,
а 5+5=5*2. Кстати, например, в Финляндии определение умножения другое: 2+2+2+2+2=5*2.
Взрослые зачастую судят с высоты своих знаний, не вникая в тему урока
а 5+5=5*2. Кстати, например, в Финляндии определение умножения другое: 2+2+2+2+2=5*2.
Взрослые зачастую судят с высоты своих знаний, не вникая в тему урока
А чё непонятного. Сложение и умножение- разные способы. А если менять местами множители, то все равно будет умножение, только один способ
Логика такая - "первым должно стоять то, что получим в результате." Пять ребят по два шарика, спрашивают про шарики, значит 2х5. В детстве снизи за такое, запомнил
раскрыть ветку (6)
раскрыть ветку (2)
Да в общем-то и костное, потому что с таким абразаванем мозг замещается сплошной костью.
Нет тут никакого "костного" мышления, это задача, там есть условия, и умножать нужно ручки на пеналы, а не пеналы на ручки.
раскрыть ветку (1)
ещё комментарии
Дурдом. Давно известно, что от перемены мест множителей произведение не меняется.
Я понял! Учителю просто надо было хоть что-нибудь начеркать в тетради!
Я понял! Учителю просто надо было хоть что-нибудь начеркать в тетради!
раскрыть ветку (7)
Есть такие понятия как множитель и множимое. Нам нужно вычислить количество ручек- это множимое. В 3 пеналах- это множитель. Это важно когда есть определения. Иначе вы получите результат не в ручках, а в пеналах. Если бы задача звучала так: «какое произведение у 7 и 3», то вы были бы правы. В таком случае перемена не важна. Так учили всегда.
раскрыть ветку (6)
Спасибо вам! Остались еще здравомыслящие. Остальные будто не слышат! И толдычат свое - «от перестановки множителей ...» /facepalm/ И, самое главное - все готовы лезть в методику и говорить как лучше и правильней.
Тогда давайте явно прописывать эти определения.
Не вижу разницы как читать: "взять по 7 ручек 3 раза" или "3 раза взять по 7 ручек".
Не вижу разницы как читать: "взять по 7 ручек 3 раза" или "3 раза взять по 7 ручек".
раскрыть ветку (1)
Juggernaut93, это действительно кажется малозначительным после старшей школы. Однако, в начальных классах в этом есть большая разница. Думаю, эта разница и обсуждалась на уроке. Поэтому такая подпись :)
что умножая 7 ручек на 3 пенала, что 3 пенала на 7 ручек, мы все ровно получим 21 ручку, т.к. знаем что ручки содержатся в пеналах, а не пеналы в ручках
раскрыть ветку (2)
Не совсем, уважаемый ArchiDeMoN. В начальных классах всегда было важно кто множитель, а кто множимое. В старших классах, это действительно не важно. Либо у вас был не самый хороший учитель, либо вы просто забыли ;)
раскрыть ветку (1)
В чем важность то? Что это меняет? Есть три фуры, с тридцатью паллетами, на них по три сотни коробок, в них три тыщи пеналов, в каждом пенале по три ручки. Похер на решение, главное результат!
И здесь есть логика. Умножил ты 5 на 2. То есть 2 раза взял по пять. А рядом взял 2 пять раз. За что и получил + и -
раскрыть ветку (4)
раскрыть ветку (3)
Не, ну доля логики есть - 2 по пол-литра или 5 по 200 мл. Во втором случае тары меньше выкидывать. Но результат все равно один - я в "дрова".
раскрыть ветку (2)
ещё комментарии
Школьный уголок
1.9K поста3.9K подписчика
Правила сообщества
Можно:
Писать всё, что можно отнести к школе.
...
Нельзя:
Нарушать правила Пикабу.