Перемена мест слагаемых6
Я бы тоже так решил. Идиотизм.
Постоянно в школе бесило это дописывание чего ты считаешь. Полная дичь. Еще и ебали мозг потому что не допишешь, что тут 5 гвоздей, а тут 3 яблока.
"сложить X предметов Y раз"
а может Y раз сложить по X предметов?
это блять не английский язык с железными правилами построения фраз - у нас оба варианты удовлетворяют допустимы.
ещё комментарии
Любая наука и особенно математика очень строгая, посмотрите определение умножения: a * b = a + a + a ... + a, (b раз). Поэтому мы берем X (множимое) предметов Y (множитель) раз и никак иначе. Операция перестановки тоже строгая: взять X предметов Y раз = взять Y предметов X раз, где предмет один и тот же.
раскрыть ветку (9)
посмотрите определение умножения
a * b = b * a
Учитывая уровень интеллекта, который вы деконстрируете... Посмотрите на картинку. Подумайте. Потом, если вам что-то еще будет непонятно, задавайте вопросы.
раскрыть ветку (1)
Да, у меня есть пару вопросов:
1. Зачем вы скидывает картинку, которую я уже скидывал? И которую я описывал ещё в другом месте на примере плитки шоколада? И которую второклассник ещё не знает?
2. Зачем вы что-то пишите об интеллекте, если сами не осиливает посмотреть пару соседних комментариев и разобраться в написанном, но зато упорно лезете с глупым утверждением?
Извините, но мне лень писать объяснение двадцать раз подряд, учитывая что у остальных проблем с пониманием не было. И я сейчас не говорю о тех, кто со мной согласен, а как раз наоборот считают данный подход в обучении(!) бредом и продолжают так считать.
Поэтому мы берем X (множимое) предметов Y (множитель)
и где тут указание на то, что тут обязательно первое, а что обязательно второе?
на английском это все например: "B times A", т.е. ровно противоположно тому, что ты пытаешься навязывать, заявляя о точности математики.
это момент - не математика, а традиция, хотя на самом деле долбоебизм.
раскрыть ветку (6)
От того, что вы взяли английский аналог, суть от этого не поменялась. Вы все равно не имеете права записывать числа по другому, если дано четкое и конкретное определение: `adding 3 copies of 4 together` - 3 раза 4. Добавьте размерность и ничего не изменилось, просто теперь записываете наоборот и учитель перечеркнет другой вариант 4 * 3 = 3 * 3 * 3 * 3 (все еще складываем пеналы, англ. вариант определения).
раскрыть ветку (5)
ты хоть сам понимаешь, что твои аргументы это: "оно так просто потому, что оно так, а не иначе"?
раскрыть ветку (4)
Мои аргументы сводятся к стандартизированному и общепринятому варианту определения. Определения в мире науки, это закон. А ваши сводятся к выводам, которые делаются на его основе, которые вы используете интуитивно. В третьем классе как раз выводы объясняются и все становится на свои места. Поэтому проблемы не в самом методе, а в том, как это организованно для второклассников.
раскрыть ветку (3)
закон в мире науки это: "от перемены слагаемых результат не меняется".
это математика.
а это "4*5 - правильно, а 5*4 неправильно" - к математике никакого отношения не имеет и равнозначно запоминанию и выучиванию бесполезных правил, не имеющих никакого отношению и к реальному миру, и к миру математики.
ещё комментарии
раскрыть ветку (1)
Множители, какая разница?
Вот при делении и вычитании - да, место имеет значение. А при сложении и умножении место значения не имеет, ибо в условиях задачи есть пояснение и уточнение, что собой являет та или иная цифра/число.
ещё комментарии
ещё комментарии
Товарищ, вводя размерность, нужно хотя бы чуточку понимать что это. У вас 4 ручки на пенал. А не просто 4 ручки. Километры в час помните? Так вот тут тоже самое. 4 ручки/пенал * 3 пенала = 12 ручек. 3 пенала * на 4 ручки/пенал = 12 ручек. Умножение коммутативно. 3*4=4*3.
С приветом, дипломированный математик.
С приветом, дипломированный математик.
раскрыть ветку (1)
Когда пишите комментарий, удостоверьтесь, что он не написан и не обсужден уже раз двадцать в соседних ветках в паре сантиметрах от ваших глаз. Это касается как размерностей, так и коммутативности, так и их применительности для второклассников. А то это показывает недалекость ума, даже не смотря на его "дипломированность".
раскрыть ветку (4)
Математическое определение умножения a * b - взять a предметов b раз: a * b = a + a + a ... + a, (b раз). Свойства перестановки тоже по другому объясняются, пеналов вы там не увидите: 4 ручки по 3 раза = 3 ручки по 4 раза. Поэтому мы получим и там и там ручки, даже если поменяем местами множители. Но пока операция перестановки не проходилась, соблюдается строгий формализм. Операция перестановки так же хорошо показана в википедии (на удивление):
Потому что пинал и ручки не математические величины, умножаем количество одних на количество других.
раскрыть ветку (2)
ещё комментарии
ещё комментарий
А почему бы не взять 3 раза по 4 ручки или 5 раз по 2 шарика, если уж так принципиально иметь "множимое"? (У нас в советской школе и слова такого не было, было множитель и множитель)
раскрыть ветку (1)
Учитывая опыт предыдущих ответов и вопросов к ним, скажу так: во втором классе сначало действует урезанное правило а * b - "взять а предметов b раз". Принципиальным это считается недолго, до того момента, пока детям не расскажут правило перестановки и это правило больше не применяют, выходя в нормальную математику. У меня тоже в школе такого не было, но кто-то решил ввести это в педагогическую практику, я же просто пояснил логику для родителей.
А то,что в выражениях коэффициент пишется перед переменной, разве не выглядит логичным? 3*х например. Я бы написала 3*4 в таком случае. Но в рамках конкретной задачи не вижу разницы в порядке записи.
раскрыть ветку (1)
На первом месте множимое, потом множитель. В любом случае после изучения перестановки можно этим не заморачиваться и ставить как хочется. Взрослые как правило даже не думают, что под этим есть формальное доказательство и логика - главное работает и ладно.
Учителя не могут объяснить детям, что такое размерность и как следствие учат хуйне. То, что вы написали - идиотизм с кучей логических ошибок, про которые ниже написали.
Как думают учителя: 3 пинала * 4 карандаша = 12 пиналокарандошов. Видят, что выглядит не очень и поэтому говорят - что финальную размерность определяет та размерность, которая идет раньше, а второю - отбрасывают.
Как надо оформлять такой пример, чтобы к нему не доебались:
3 пинала * 4 карандаша/пинал = 12 карандашей.
Над размерностью производят те же операции, что и над самими значениями.
В действительности, все объяснения умножения через сложения справедливы только для безразмерных натуральных чисел.
Я бы посмотрел как учитель будет объяснять таким образом что-то такое:
15,5(км/ч) * 185 (мин).
раскрыть ветку (6)
Согласен.
Единственное они не могут написать размерность карандаша/пинал т.к. деление и сокращение дробей к этому моменту не пройдено. Поэтому поясняют как могут, потом тут же давая правило перестановки и выходя на нормальное умножение.
раскрыть ветку (5)
Поправить программу и давать все последовательно, объяснить детям как работают размерности? да не бред какой-то, лучше будем врать и учить их тому, что противоречит законам математики. 10из10
раскрыть ветку (4)
Я бы посмотрел, как вы бы им это объясняли) Проще вообще работать без размерностей, чем потом копаться в болоте таких размерностей.
P.S. На данный момент ничего законам математики не противоречит, а используются допущения и упрощения, которые потом расширяются до нормальных рамок. Вас же устраивает, что учитель в начальных классах без объяснений зачеркивает вычитание из меньшего числа большего т.к. ребенок еще не знает отрицательных чисел. Или говорит, что корня из отрицательного числа не существует, а потом ему суют комплексные числа.
раскрыть ветку (3)
Нет, меня не устраивает. Я объяснял детям и не такое.
Правильно, кому-то проще, и пофиг на детей.
Противоречие в том, что запрещена коммутативная операция.
раскрыть ветку (2)
Моей целью было донести до родителей, что во втором классе действует правило а * b - "взять а предметов b раз", которое потом экстраполируется в нормальную алгебру. Возможно, это поможет им преодолеть трудности, которые возникают из-за непонимания логики учителей. Настаивать на правильности этого подхода в обучении я не собираюсь, поэтому ничего не имею против ваших рассуждений.
раскрыть ветку (1)
Я вас понял. И с вами согласен, но делали вы совершенно иное. В вашем объяснении не упомянуты те самые упущения из-за которых весь кипиш и фактически оно неверное. Когда ошибки были выявлены, вы сказали, что малышам они будут непонятны, но при этом само объяснение было рассчитано на родителей.
Если вы преследовали эту цель, то вам надо было изложить все теорию со всеми допущениями и ошибками. А решение уже бы принимали родители. Да и логика учителя здесь не причем, а только его лень, либо отсутствие квалификации.
Не надо воспринимать такие вещи как норму, иначе нам всем будет жопа.
Ну да - подловил учителя в тёмном переулке, отпиздил его , напевая под нос "каждому лектору в жопу по вектору" и проходит такой недуг у проводника к знаниям.
раскрыть ветку (1)
да нет, ваши дети тоже так учились. и вы так учились - это всегда требовалось в арифметике. Мы узнаем. сколько было карандашей? значит, карандаши умножаем на коробки, не наоборот. Ну такое правило. Учитель должен требовать это от учеников.
Задание номер 4 вроде не полностью сделано (там в см и мм надо было измерить), но там +. А за правильный математический пример +-. Где там логика?
По мне, так 5 * 2 как раз по тексту задания, т.к. У 5 ребят по 2 шарика = 5 самцов
Потому как 2 * 5 это, По 2 шарика у 5 ребят
раскрыть ветку (28)
5*2=5+5
2*5=2+2+2+2+2
Детей учат не только умножать, но и понимать, что они умножают и зачем.
Это когда вы считаете ребят с яблоками - в общем-то пофиг, что на что умножать. А когда вы начнете считать, сколько вариантов у пяти детей выбрать по пять яблок из пяти сортов, расположенных определенным образом в 5 корзинах...
раскрыть ветку (27)
Но ведь у 5 ребят по 2 шарика, т.е. 5*2=2+2+2+2+2. Разницы никакой. Чисто субъективное восприятие человека. Не стоит оправдывать этот идиотизм.
ещё комментарии
раскрыть ветку (14)
Кто это решил? Это все ещё 5 ребят и 2 шарика у каждого. Просто один "умник" решил что такое написание будет значить "два раза по пять", а не "пять раз по два", хотя последнее даже звучит логичнее. Вы ведете себя как радикалы какие-то. Любое инакомыслие пресекается на корню, вместо того, чтобы объяснить что это одно из верных решений. Жаль что у нас в школах есть такие люди.
раскрыть ветку (8)
Все верно, по скольку у каждого было по два шарика, а ребят было пять, то что мне мешает 2х5. Это и называется логика. Ребенок ведь в ответе написал 2+2+2+2+2=10, где ошибка?
Собственно, примерно это я и хотел сказать.
А так у многих возможно и появляется машинальное желание написать 5 * 2 из-за построения текста задания. Конечно, задание вида "У каждого мальчика по 2 шарика. Мальчиков 5. Сколько у них шариков?" Выглядит корявее, но явно располагает необходимые акценты и больше захочется написать 2 * 5 уже.
Вот если бы при этом всём привели конкретную формулу вида:
предмет(или его количество) * сколько раз = общее число предмета
то многие не спорили, т.к. многие не знают конкретные требования, а как кому-то кажется что есть только один вариант записи - это бред. Как условишься, так и будет. Так-то всё вокруг нас состоит из условностей, и речь и прочее, но это не говорит о том что так делают все. Не все пишут же буквы одним и тем же способом.
Возможно, некоторые дети понимают суть, но восприятие "раз * что-то", для них лучше чем "что-то * раз". И менять это, как левшу правой рукой заставлять писать - будет каждый раз дёргаться сначала левой рукой, потом внутренне ломать свой естественный уклад и через силу заставлять делать это медленно, коряво, получая стресс. В данном случае надо донести суть на уроке, а задания или соответствующие главы с заданиями должны содержать конкретные требования. При этом, лучше делать пометку, что необходима конкретная запись(ссылка на главу), чтоб у ребёнка, который мыслит иначе не возникало каши от того, какой вариант надо, т.к. для него правилен один вариант, но он начнёт сомневаться что ошибся, как результат - получит худшее восприятие темы и багажом ещё начнёт развивать в себе неуверенность. В лучшем случае такого ребёнка достанет нападки, что он всё делает не так, и он начнёт ни во что не ставить чужое мнение и плевать на него, в худшем - получим тупящщего, тормозящего и неуверенного и замкнутого в себе.
Кто это решил?
Скорее всего греки. Множитель это то, что стоит вторым. Множимое - ставится первым. По определению. Всем похуй что ты считаешь иначе. Иди создавай свою математику, со своими правилами и доказывай что она лучше нынешней.
@MarisaChan ну и тебе тоже заодно.
раскрыть ветку (5)
множимое? што?
ок, допустим это не бред героинового наркомана.
в двух вагонах поезда едут по пять мальчиков, каждый из которых держит по 2 шарика. сколько шариков едет в подвижном составе?
ну ка, давай ка расскажи мне, как называется число, которое стоит третьим?
а если ещё чисел в умножении добавить?
раскрыть ветку (2)
Ну тоже логика не самая. Действия производятся по порядку. Соответственно, участвуют одновременно лишь два члена уравнения. С остальным согласен.
Мдаа, человек не способный уловить такую простую мысль высирает аргументы на уровне "шах и мат атеисты".
Там нет третьего числа, ибо ты не перемножаешь три значения одновременно. Ты в любом случае умножаешь только два. Например находя общее количество мальчиков, а затем выполняя действие по шарикам.
а вот ещё тебе задачка.
сила, изменяющая за 1 секунду скорость тела массой 1 кг на 1 м/с в направлении действия силы давит на один квадратный метр поверхности.
сколько паскаль давление?
что у нас тут по твоему определению множимое, а что множитель, и как называются остальные величины, раз у тебя названия есть только для двух.
Свою математику?) Вы пишете ерунду, одно из основных и элементарных правил математики: "От перемены мест множителей произведение не меняется". Это не я придумал. А вот ту чушь, которую вы защищаете, придумали точно не греки.
Какая такая логика так говорит? Сложение должно в голове происходить у ребенка на начальных этапах. 5*2 или 2*5 не важно, он просто представляет себе 5 детей с 2 шариками у каждого и все. Запись не должна играть роли в данном случае.
раскрыть ветку (4)
Школьная логика говорит о том, что первое число в таких выражениях идет то, что берем, а второе то, сколько раз берем первое. При этом ребенок может прекрасно осознавать что и как, но критически мыслить программа обучения не дает, однако критически мыслит не много ребят, так что идти поперек правил зачастую бессмысленно, все зависит от конкретных ситуаций. Как сам помню, были преподаватели, которые позволяли отходить от правил в расчетах. Зная, что ученик прекрасно понимает то, что считает.
раскрыть ветку (3)
Что за бред? Какая разница 5 раз берем 2 шарика или 2 шарика берем 5 раз? Кольцо целых чисел коммутативно по умножению, какая разница-то? Некоммутативные кольца вообще в школе, емнип, не проходят!
раскрыть ветку (1)
Ну и что кто берет?
5 мальчиков, 2 шарика.
Берем 2 шарика по 5 раз, или у 5 мальчиков по 2 шарика ?
Мы сами выбираем множитель. Либо количество пацанов, либо количество шаров у каждого поцана.
ещё комментарии
Ты явно не прав и в школе учился плохо, потому что на самом деле вот так:
5*2 = 2+2+2+2+2
2*5 = 5+5
А то, что ты написал это ересь и вообще не по канону. И поэтому тебя нужно сжечь, даже если ты красивый.
раскрыть ветку (9)
Как раз не правы вы.
Умножить некоторое число (множимое) на целое число (множитель) — значит повторить множимое слагаемое столько раз, сколько указывает множитель.
раскрыть ветку (3)
Я утверждаю, что множитель в данной записи стоит первым, что даже нашло отражение в особенностях и стилистике русской речи: "пять раз по два".
Я подожду ваших опровержений, хотя и утверждать обратное есть попрание всех основ, форменное издевательство и вообще!
раскрыть ветку (1)
Мы сами выбираем множитель. Либо количество пацанов, либо количество шаров у каждого поцана.
ещё комментарии
Вы не правы. На правах кандидата технических наук заявляю, что a*b - это b раз просуммированное a.
раскрыть ветку (4)
ещё комментарии
реально дичь какуюто несешь, ответь, почему 5*2 произносят как "пятью два"? потому что пять раз по два... таблицу умножения помнишь как учил?
ещё комментарии
раскрыть ветку (2)
Бред. Математика это инструмент для получения результата и не имеет значения к какому в прикладном плане этот результат имеет отношение. Тот кто решает задачу используя математические действия изначально понимает к чему полученный результат имеет отношение. По этому для решения любых задач математическими инструментами не имеет значения к каком понятию привязано то или иное число. Значение имеет только результат. Все остальное-чушь. 5 вилок в 3 коробах. Сколько всего вилок? Ответ вы получите в вилках, независимо от того как вы оформите решение задачи.
Интерсно какой дегенерат это написал?) Это как минимум математически неправильно, т.к. мы исключаем коммутативность операции умножения.
Очень сильно бомбил от этого. Жена сказала не бомбить, а дочке сказала, просто ставь вперед то, что ищешь. Но вот прошло полгода, я заметил, что училка уже хуй кладет на то, какое число впереди. А в начале года прям пиздец был.
раскрыть ветку (1)
а отрезок в миллиметрах ни учитель, ни ученики посчитать так и не смогли? т.к исправлений нет
Я конечно с вами согласен... Но думаю, вопрос был сколько всего шариков, в итоге нужно 2 шарика умножить на 5 ребят. А учитель посчитал что 5 ребят умноженное на количество шариков это не правильно.
Ну в хрень какая то все равно
Ну в хрень какая то все равно
раскрыть ветку (4)
Если вам сказали квадратное катить, а круглое нести - это еще не означает, что вы в армии... Возможно, вы еще в школе :)
Ваша проблема в том, что вы ШАРИКИ умножаете на РЕБЯТ, а умножать нужно КОЛИЧЕСТВО шариков на то КОЛИЧЕСТВО раз, сколько их нужно взять.
И тогда никаких проблем взять пять раз по два шарика или по два шарика взять пять раз.
Если у той училки в голове тоже шарики на ребят умножаются, то у нее проблемы с головой и ее точно из школы гнать надо.
раскрыть ветку (2)
Тоже подумал сначала гнать, но теперь я хоть ее логику уловил. Может быть это проф деформация, поскольку как раз дети могут не понимать почему одно на другое умножается.
Дочка вчера тоже четверку принесла. В учебнике написано 600х350, а ребенок умножил 350 на 600. Умножение в столбик, у учителя видимо шаблон не сошелся.
раскрыть ветку (3)
Причём подобный вариант даже проще при умножении руками, ребёнка похвалить только за оптимизацию.
раскрыть ветку (2)
Тут на днях с ребенком степь рисовали, нарисовали юрту, лошадок травку зелёную, двойку принесла. А ведь всей семьей сидели , думали , как бы по красивше сделать. Даже подписали - Калмыкия ( Мы Мурманчане ) Предмет, "Окружающий мир" Учитель сказал, что степь должна быть желтая. И ниипет!))
Думаю, логика тут в том, что первым должно идти кол-во шариков, т.к. вычислить надо именно их. В заглавном посте то же самое - раз надо узнать, сколько ручек, исходное количество ручек ставится на первую позицию. Для взрослого, конечно, бред, но мы уже умеем умножать, а ребенок только учит сам принцип.
раскрыть ветку (1)
Учился в школе с 1993 по 2003 и нас точно так же заставляли располагать множители, так что это не какой-то новый тренд )
раскрыть ветку (1)
Пффф! 93-2003...
Это "правило" было сформулировано ещё в советском методическом пособии для обучения начальных классов лет 60 назад. К сожалению, не могу вспомнить автора, встречал пару лет назад в сети.
Я тут кстати сильно думал над этим и вспомнил. В первом классе у нас требовали, чтобы вот в таких вот примерах первым множителем был тот, который будет стоять после равно. Т.е. если считаешь шарики а коробках, то шарики*коробки=шарики. И тоже пару раз ловил минусы за это, благо во втором классе я перешел в другую школу. И там была такая же херня, так как ебучий Петерсон
раскрыть ветку (1)
и самое интересное, что это правило вырабатывают, а потом на него хуй кладут к классам повыше. и поступив в вуз, кладите хуй на школу.
а на работе - вообще кладите хуй на все (у нас тут свои правила) = замечательная система.
Там просто учится табличка на 2. Должны были разные что подчеркнуть и на уроке объяснить, что не надо спешить и надо пока разобраться с табличкой на 2. Или если и перечеркивать, то не отнимать балл.
раскрыть ветку (1)
Скорее дополнительно побеседовать с ребёнком, чтоб удостовериться, что он понял суть данного действа. Пусть сам проговорит свои записи.
Так в школе же обучали этому. То, что считаем - должно быть на первом месте. Количество на втором. То есть например нам надо посчитать, шарики у ребят: шарикиуодного*количестворебят=шарикиувсех
раскрыть ветку (1)
а когда смету в строительстве считаешь, все наоборот, сначало количество того что считаем, а потом сколько за штуку... сам удивился когда столкнулся, но оказывается все просто, так проще спецификации из проекта в сметы в екселе переводить
Ну здесь то хоть понятно. Вторым способом расписали как 2*5. При первом примере надо было 5+5=10.
раскрыть ветку (2)
Пять ребят по два шарика, где вы 5+5 нарыли? Видать вы такой же учитель как в примере )) Ну разве что пять шариков в левой руке плюс 5 шариков в правой руке, но это вообще уже за гранью понимания...
раскрыть ветку (1)
Первая переменная - ребяты с шариками, их 5, затем считаем, сколько шариков у каждого, их 2, соответственно слагаемых пятерок будет так же 2. Можно сделать и 2+2+2+2+2 и 5+5. Разницы в результате нет, есть разница в логике, которая помогла придти к результату, но оба варианта верные.
Взяли 2 шарика 5 раз, не 5 шариков 2 раза... Это в примерах по фиг перестановка мест множителей, а в задачах строго... Взять что то столько то раз... Это как мне учительница начальных обьяснила
раскрыть ветку (1)
а почему нельзя взять 5 человек по 2 шарика?)
или 2 шарика по 5 человек ( второе даже звучит убого )
Потому что сейчас они должны понять логику умножения, а не просто заучить табличку. 2*5 - это два взять пять раз. Да, оно равно 5*2, но смысл теряется. Точно так же, если бы он в первом примере написал 3*8=24, это было бы неправильно с точки зрения логики преобразования сложения в умножение. Не 3 сложенное 8 раз, но 8 - трижды
Тут знакомой, похоже, надо к директору, а если тот не поможет, то в РОНО обращаться, пидорская, блять, училка, у меня в свое время любовь к географии одна падла отбила...
раскрыть ветку (1)
На порядок умножения обращают внимание именно в начальной школе, когда изучают принцип умножения. Понять принцип или тупо заучить, ничего не понимая - это совершенно разные вещи. Взрослые из-за того, что уже забыли такие мелочи из начальной школы и могут не задумываясь, на автомате умножать, делить недоумевают " а какая разница?" и детям говорят "вот училка не правильно вас учит". А учительница учит по методике, которая не менялась с советских времён.
раскрыть ветку (18)
учительница учит по методике, которая не менялась с советских времён.
Когда сразу учили:
"От перемены мест слагаемых сумма не меняется."
И
"От перемены мест множителей произведение не меняется."
И таким бредом как сейчас не занимались.
"От перестановки мест множителей произведение не меняется"©
"От перестановки мест слагаемых сумма не меняется"©
Вот это - методика советских времен. До сих пор от зубов отскакивает.
А то что вы пишите - херня из под коня, а не "советская методика".
ещё комментарии
при чем тут перестановка? Учат понимать смысл написанного, а не тупое знание. Знаешь чем отличает ум от интеллекта? В том, что ты не просто знаешь, что 5х2 = 2х5, а в том, что ты знаешь чем отличается 5 по 2 и 2 по 5
раскрыть ветку (9)
ещё комментарии
Дело не только в математике, тебя учат правильно воспринимать информацию, описанную в задаче, а не оперировать только абстрактными числами
раскрыть ветку (2)
Дело в математике. И её учат именно для того чтобы понимать что "3 пенала по 4 ручки" и "4 пенала по 3 ручки" - это одно и тоже количество ручек.
Чтобы потом в магазине не думать что 4 пачки %продукта% по 250 грамм это лучше чем 2 по 500.
Ну и? 5 ребят имеют по 2 шарика или по 2 шарика у 5 ребят. Хоть как меняй местами и умножай, сути не меняет.
Для примера из поста:
3 пенала умножить на 4 = 12 пеналов
4 ручки умножить 3 = 12 ручек
Смысл поменялся, не правда ли?
раскрыть ветку (4)
Я бы ща доколупался что вы "для примера" одну единицу измерения выбросили а другую оставили.
Но вам потом на физике в 6-м классе за это по голове дадут.
а если немного подключить мозги, то получим следующее:
3 пенала умножить на 4 ручки = 12 ручек
4 ручки умножить на 3 пенала = 12 ручек.
ещё комментарии
ещё комментарии
Определение. Умножение — это действие в результате которого находят сумму одинаковых слагаемых. Умножить число а на число Ь означает найти сумму Ь слагаемых, каждое из которых равно а.
но какой от этого смысл, если.
Переместительный закон
Правило. От перестановки множителей произведение не изменяется.
Я ещё понимаю, если были задачи посложнее, где были бы выявлены существенные ошибки в ответе при не правильном применении умножения\деления.
Но цель найти количество ручек, хоть как умножай ответ будет один, ведь при умножении количества пеналов с ручками на количество ручек в этих пеналах мы не получаем пеналы, мы получаем ручки.
к сожалению, но большинство, "взрослых" комментаторов на пикабу этого не понимает, так как каждый считает себя "умным", а потом дети получают полтора землекопа!
раскрыть ветку (2)
вы бы хоть пояснили какое отношение ваши «полтора землекопа» имеют к порядку записи коммутативных операций?
Если вы решите апеллировать к единицам измерения, то будете неправы ибо умножаются единицы вида чел. * шарики/чел.
Какая разница как считать, если ты под ответ полтора подвел землекопов, которые всегда натуральные? Почему бы просто не сказать писать 1.5(ям). И правила соблюдаешь и голову включаешь.
Вроде бы эти методики каждый год обновляются, не? По одной и той же методике у нас только преподаватели-пенсионеры учат...
раскрыть ветку (1)
ещё комментарии
ещё комментарии
Логично что от перестановки сумма не меняется- это мы уже давно поняли. Тут есть такая тонкость что отталкиваться нужно от шариков и мы видим что логичней и примитивней сумму прописать как 2+2+2+2+2=10(2*5, два шарика плюс два шарика и т.д.), писать сумму как 5+5=10(5*2) вообще не логично в данной задаче для школьника(пять ребят плюс пять ребят, а шары где?))) ) . Повторюсь, от перестановки сумма не меняется, но логику умножения правильна в ответе 2*5 если отталкиваться от суммы.
раскрыть ветку (5)
Тут логика в другом. Вы сможете доказать что а*b=b*a? Боюсь что не сразу, потому и умножать нужно так как научили. Как только вы сможете учителю доказать коммутативность умножения - умножайте как хотите.
раскрыть ветку (4)
Коммутативность операций сложения и умножения это аксиомы арифметики. Умножение по определению коммутативно, это не нужно доказывать. Раньше в школе изначально этому учили, от перемены мест слагаемых сумма не меняется, то же самое и для умножения. Как раз на данном конкретном примере это можно было бы отлично показать. Да, по определению 5*2=5+5, 2*5=2+2+2+2+2, но так как от перемены мест множителей произведение не меняется, то вы можете писать в любом порядке и это будет правильно. Перечеркивание ответа и снижение оценки вызывает больше вопросов и негатива, а пользы никакой не несет.
раскрыть ветку (3)
Извините конечно, но ваши познания в математике на уровне Занусси, с их шедевральным "параллельные прямые не пересекаются. Доказано Евклидом".
Что бы не быть голословным, пример когда умножение некоммутативно - матрицы.
раскрыть ветку (2)
В арифметике умножение коммутативно, это аксиома. В евклидовой геометрии параллельные прямые не пересекаются, следствие пятой аксиомы.
Я вашу точку зрения понял, дальше нет смысла спорить.
раскрыть ветку (1)
Параллельные прямые не пересекаются - это постулат, предположение. На этом предположении основывается евклидова геометрия. Неевклидова, например Лобачевского, обходится без этого постулата.
Постулат != Аксиома.
Выше привёл вам пример, арифметика матриц, где умножение некоммутативно.
почему они зачеркивают? что, там у 2 шариков по 5 ребят? как они это объясняют детям? и не действует ли правило от перемены мест ?
Чето я нихуя не понял. Первым же идет число пять, поэтому правильно 5 на 2. Или нужно было еси 5*2 пишешь, то писать потом 5+5?
Я не согласен с учителем. В задаче Ф3 сказано в такой последовательности: у 5 ребят по 2 воздушных шарика. Значит и решение в автоматически пишется соответственно 5*2.
Тут что-то типо если спрашивают сколько шариков, то нужно сначала шарики брать и умножать на число. Зачем это не совсем понятно, может как-то заранее готовят к единицам измерения
Когда я училась в школе, нам учитель объясняла, что нужно умножать предмет на количество человек, если нужно узнать кол-во предметов, если наоборот, то это будет кол-во человеков. Если бы это был пример, а не задача, то перемена мест слагаемых роли бы не играла
Я разгадал ее логику: во всех примерах выше первым идёт то число, которое повторяется при записи сложения (3+3+3+3+3 -> 3*5). В примере три несколько раз повторяется двойка (2 шарика пять раз), поэтому 2*5. С точки зрения математики ставить ошибку здесь бред, но логика кажется такая. Может им дали конкретный алгоритм решения задачи и теперь проверяют знание алгоритма, а не ответ?
всё верно, первым идёт то, что нужно посчитать. с ложении перестановка слагаемых возможно тк подразумевается объединение двух однотипных слагаемых. в то время, как в умножении разнотипные. потом в ответе и пишут "10 шариков", а не просто 10
С нельзя с этим решением к учителю подойти и уточнить, в чем прикол и за что снизили?
Послушать аргументы.
А-то как обычно двояко. Вроде и бред снижать за это.
С др стороны, смотря как проходят по программе.
Наша учитель была лояльна и закрывала глаза на такое. Но это было лет 20 назад уже.
Послушать аргументы.
А-то как обычно двояко. Вроде и бред снижать за это.
С др стороны, смотря как проходят по программе.
Наша учитель была лояльна и закрывала глаза на такое. Но это было лет 20 назад уже.
А если бы он написал 5·2=10; 5+5=10, что бы поставили? У пяти ребят есть по одному шарику и ещё по одному шарику — всего 10. Судя по предыдущему, порядок сомножителей такой же как в фразе "слагаемое x повторяется y раз" = x·y
Уже много таких примеров было. И учитель здесь прав. Это определение действия умножения и на данном этапе порядок произведения важен. То есть 2+2+2+2+2=2*5,
а 5+5=5*2. Кстати, например, в Финляндии определение умножения другое: 2+2+2+2+2=5*2.
Взрослые зачастую судят с высоты своих знаний, не вникая в тему урока
а 5+5=5*2. Кстати, например, в Финляндии определение умножения другое: 2+2+2+2+2=5*2.
Взрослые зачастую судят с высоты своих знаний, не вникая в тему урока
А чё непонятного. Сложение и умножение- разные способы. А если менять местами множители, то все равно будет умножение, только один способ
Логика такая - "первым должно стоять то, что получим в результате." Пять ребят по два шарика, спрашивают про шарики, значит 2х5. В детстве снизи за такое, запомнил
раскрыть ветку (6)
раскрыть ветку (2)
Да в общем-то и костное, потому что с таким абразаванем мозг замещается сплошной костью.
Нет тут никакого "костного" мышления, это задача, там есть условия, и умножать нужно ручки на пеналы, а не пеналы на ручки.
раскрыть ветку (1)
ещё комментарии
Дурдом. Давно известно, что от перемены мест множителей произведение не меняется.
Я понял! Учителю просто надо было хоть что-нибудь начеркать в тетради!
Я понял! Учителю просто надо было хоть что-нибудь начеркать в тетради!
раскрыть ветку (7)
Есть такие понятия как множитель и множимое. Нам нужно вычислить количество ручек- это множимое. В 3 пеналах- это множитель. Это важно когда есть определения. Иначе вы получите результат не в ручках, а в пеналах. Если бы задача звучала так: «какое произведение у 7 и 3», то вы были бы правы. В таком случае перемена не важна. Так учили всегда.
раскрыть ветку (6)
Спасибо вам! Остались еще здравомыслящие. Остальные будто не слышат! И толдычат свое - «от перестановки множителей ...» /facepalm/ И, самое главное - все готовы лезть в методику и говорить как лучше и правильней.
Тогда давайте явно прописывать эти определения.
Не вижу разницы как читать: "взять по 7 ручек 3 раза" или "3 раза взять по 7 ручек".
Не вижу разницы как читать: "взять по 7 ручек 3 раза" или "3 раза взять по 7 ручек".
раскрыть ветку (1)
Juggernaut93, это действительно кажется малозначительным после старшей школы. Однако, в начальных классах в этом есть большая разница. Думаю, эта разница и обсуждалась на уроке. Поэтому такая подпись :)
что умножая 7 ручек на 3 пенала, что 3 пенала на 7 ручек, мы все ровно получим 21 ручку, т.к. знаем что ручки содержатся в пеналах, а не пеналы в ручках
раскрыть ветку (2)
Не совсем, уважаемый ArchiDeMoN. В начальных классах всегда было важно кто множитель, а кто множимое. В старших классах, это действительно не важно. Либо у вас был не самый хороший учитель, либо вы просто забыли ;)
раскрыть ветку (1)
В чем важность то? Что это меняет? Есть три фуры, с тридцатью паллетами, на них по три сотни коробок, в них три тыщи пеналов, в каждом пенале по три ручки. Похер на решение, главное результат!
И здесь есть логика. Умножил ты 5 на 2. То есть 2 раза взял по пять. А рядом взял 2 пять раз. За что и получил + и -
раскрыть ветку (8)
раскрыть ветку (5)
Не, ну доля логики есть - 2 по пол-литра или 5 по 200 мл. Во втором случае тары меньше выкидывать. Но результат все равно один - я в "дрова".
раскрыть ветку (2)
Попробуй поднять одной рукой над головой килограммовую гирю 100 раз, а затем 100 килограммовую гирю один раз, тогда поймешь логику.
Задачки вырваны из контекста. Это для взрослых понятно, что от перестановки множителей сумма не меняется. Детей на уроке учат (должны) как правильно мыслить, чтобы задачу превратить в математическое решение, и здесь они должны отработать именно это. От простого к сложному, а потом уже вводить более абстрактные операции.
Умножение - это упрощенное сложение.
Вот человек правильно пишет: #comment_135003914
раскрыть ветку (1)
И каким боком это учит правильно мыслить? Как раз наоборот, таким поведением учителя тупо вдалбливают алгоритм. И если ребенок сам догадался до коммутативности умноженния, снижение за это оценки как раз отбивает желание думать о чем-то еще.
ещё комментарии
Все проблемы решаются введением размерности. 2- ручки 5 безразмерный коэффициент. Переставлять сколько угодно.
ещё комментарии
В моё время так не учили, но сейчас совершенно чётко прослеживается логика - есть умножаемое и умножитель (только что придумал, сильно не пинайте). Умножаемое имеет натуральное представление (яблоки, ручки, велосипеды), а умножитель - просто сколько раз представлено умножаемое. 2+2+2+2+2 = 2 яблока 5 раз = 2*5. Детей учат мыслить, им потом легче будет, когда в физике (а физика - это математика в применении к натуральному миру) появятся единицы измерения и нужно будет чётко понимать, откуда какая нога растёт. Иначе будут плавать - то ли метры делить секунды, толи секунды на метры. То ли перемножить всё. А при осознании того, что скорость = м/с видно сразу, что метры на секунды = S/t :)
Когда нет чёткости - возникают разброд и шатания. В общем, всё правильно учитель делает. Я за.
Антоша, 38 годиков.
PS комменты ниже, я, конечно, не читал :)
А почему нужно умножать два на пять, а не пять на два? Учебник ну или учитель хоть какую-то логику по этому поводу приводит?
У меня дочка во втором классе, она комментирует:нас учат так-первым ставят то число, которое ищут. Если ищем число ручек, то первым пишем количество ручек - 4.
(мне тоже кажется, что это ерунда, но если этого требует программа, то пусть пишет, как сказали на уроке))
Даже ребенок понимает, что тут либо придираются к нему, либо учитель - неуч. Или долбоёб. И сразу тяга к знаниям пропадает. И что это с тобой случилось, говорит этот же учитель?!
Это не новая практика. Правда, в моем детстве это использовали как способ давления на родителей, которые почему-то не нравятся классной даме в начальной школе. При этом если ученик, у семьи которого проблем с ней нет, решал так же, ему ставили полный балл.
На выходе получилась ситуация, когда ты что-то делаешь или ты нечего не делаешь - все равно получаешь 3. Потому что два она тебе поставить не может - за четверть выйдет два и будет педсовет, где выясниться, что оценивает она знания не объективно. Так что если результат один, зачем напрягаться? И так по всем предметам.
раскрыть ветку (1)
раскрыть ветку (2)
раскрыть ветку (1)
Ну, разборки бы точно устроил бы. Идиотизм и не знание материала, который преподаешь.
Минусы наверно учителя поставили, которые не видят проблемы в фотографии выше...
Минусы наверно учителя поставили, которые не видят проблемы в фотографии выше...
ещё комментарии
Вот у нас в классе была девочка которая все 11 лет сидела за партой как овощ, ничего не понимая и не пытаясь понять. Угадайте кто стал учителем?
Я очень надеюсь, что ваша знакомая из тех матерей, которые не будут говорить сыну, что он тупой, а забьют на оценки, если учителя идиоты.
Я подозреваю, что тут задание на закрепление правила о перемене мест слагаемых. А ребёнок сделал по своему, не использую это правило. А у учителя своя программа она должна объяснить, закрепить и проверить.
раскрыть ветку (2)
А еще задание 4 решено не полностью, но препод не заметил. Так что в итоге все равно оценка адекватная.
раскрыть ветку (1)
ещё комментарии
Это у взрослых для умножения действуют сочетательные свойства умножения (специально), а в начальной школе детей третируют, если они множители местами переставляют.... сказочный идиотизм. Цитируем Лаврова.
Чо сука самый умный? Сказано 2 на 5 а не наоборот. Какие законы? Да в рот я их ебала. Делай как говорят и не выделялся.
Ебучий совок в бошках.
Мне вот интересно, а родители в общем чате пишут об этом? Например «ИО классного руководителя, это что за хрень? (Скрин картинки) У вас там математичка математику сама-то знает?
а еще можно 5 первых шариков+ 5 вторых шариков= 10 шариков.
Или у вас так за сраную четверку во втором классе горит?
раскрыть ветку (9)
У нас учитель алгебры поменялся в 10 классе.
Я по привычке очевидные вычисления пропускаю и решаю задачку быстрее всех, за что учитель поставил мне тройку.
Пошел спрашивать что не так - говорит нужно каждый шаг записывать (грубо говоря 2*5+7*3 = 10 + 21 = 31, а я записал 2*5+7*3=31).
Я спросил "а зачем? и так же все понятно", на что получил "нужно".
Правда потом он привык что я пропускаю некоторые вычисления, которые в уме легко сделать, и не снижал за это оценки.
раскрыть ветку (4)
Вау! Ну прям один в один мой случай. Только у нас была учительница и поставила она четверку. И она тоже быстро привыкла к тому, что я действительно могу все это сокращать в уме. Правда для соседа иногда приходилось расписывать подробнее в его варианте решения задач - она точно не поверила бы, что это он сам так решал.
ну ты не путай десятый класс и второй.. мне моя математичка даже за неправильные вычисления не снижала например
раскрыть ветку (2)
Ну согласись в 10 классе расписывать как ты складывал два числа умноженных друг на друга это немного глупо.
Особенно когда речь идет уже о вычислениях интегралов и логарифмов.
раскрыть ветку (1)
ну в общем-то да, даже на егэ (в мой год, во всяком случае) подразумевается, что ученик в состоянии в уме решить АЖ КВАДРАТНОЕ УРАВНЕНИЕ
ещё комментарии
ещё комментарии
ваше решение или ребёнка?
детей учат понимать, что они считают, это начальные классы, вам это написали, чтобы он умножал правильно и понимал, что он считает шарики, а не ребят, дети не думают цифрами, их учат воспринимать их правильно
раскрыть ветку (1)
я специально написал тупорылое решение, что б было понятно, что ВО ВТОРОМ КЛАССЕ в этой задаче 2*5 более правильно, чем 5*2
ещё комментарии
ещё комментарии
Да, у меня 1 и 3 классы, порой так завернул задачу, что сам сижу и думаю что они хотят от детей.
Умножить число а на число б значит число а слагаемым б раз. Т.е. 3*4=3+3+3+3, а 4*3=4+4+4.
Все логично. Это математика. Тут нужно действовать по правилам. Потом уже узнают что 3+3+3+3=4+4+4=3*4=4*3=12
И назовут эту магию "переместительным законом умножения"
И на само деле это важно, иначе не будет понимания математики а будут механические манипуляции и заучивание.
раскрыть ветку (81)
раскрыть ветку (13)
раскрыть ветку (11)
откуда такое слово взяли-"множимое". Меня сразу учили что есть два множителя. И 3*4 это 3+3+3+3 или 4+4+4. Зачем давать лишную бесполезную информацию?
раскрыть ветку (10)
"два множителя" это упрощение, связанное с коммутативностью умножения в поле скалярных величин, которое приведет к ошибкам впоследствии. Когда два множителя перестанут быть равнозначными, будет тяжело в них не путаться.
Как правильно вычислить момент силы? Сила*плечо или плечо*сила?
раскрыть ветку (7)
Момент силы вычисляется из его определения. Это уже пошло словоблудие. А записать можно в любом порядке. Иногда даже удобней сгруппировать в неканонической записи, чтоб наглядней выглядело, для дальнейших выкладок.
ещё комментарии
В том-то и дело, что от порядка записи зависит знак выражения, и если изначально не научить человека тому, что этот порядок важен, у него будут возникать глупые ошибки
раскрыть ветку (5)
раскрыть ветку (4)
Дело в том, что при векторном произведении условно говоря минус на плюс будет минус, а плюс на минус будет плюс.
То есть [ab] = -[ba]
раскрыть ветку (3)
ещё комментарии
Так, для натуральных чисел умножение определяется как многократное сложение — чтобы умножить число a на число b надо сложить b чисел a
Ну и вы наверное не разгоняли процессоры в молодости :) Там уж множитель это одно, а множимое - другое.
раскрыть ветку (1)
Но мы сейчас говорим про начальную школу, где дети должны усвоить основные правила. А от избытка лишней информации у них будет одна каша в голове.
ещё комментарии
ещё комментарии
Мешает вот что. Если уж совсем упрощенно, то умножение выглядит так:
одинаковое слагаемое * сколько раз оно повторяется. При решении задач (при незнании переместит.закона умножения) это принципиально.
одинаковое слагаемое * сколько раз оно повторяется. При решении задач (при незнании переместит.закона умножения) это принципиально.
И на само деле это важно, иначе не будет понимания математики а будут механические манипуляции и заучивание.
А если ребенок уже знает про коммутативность умножения? Все равно неправильно?
раскрыть ветку (18)
У меня как-то в школе не засчитали задачу по геометрии, потому что я в ней применял правила, которые "мы еще не проходили". Ох у меня пригорало тогда.
раскрыть ветку (5)
У тебя проверяли знания текущих правил. Учителю важно понимать усвоен ли текущий материал. Нормальному учителю зачастую не важен ответ, ему важен ход решения.
раскрыть ветку (1)
Вот это тоже знакомая тема. Цель заданий в школе не получить результат, а просто вдолбить в голову ученика тему. Имхо это неправильно. Человека нужно учить оценивать любую задачу, искать оптимальное решение.
раскрыть ветку (2)
1. Способов решения задачи всегда несколько. Если в задаче не указано каким способом ее решать, то могу решать любым.
2. Был очень демотивирующий эффект на чтение учебника дальше положенного. Я понял, что если я учу что-то сам, то должен запоминать что мы проходили в школе, а что я читаю сам.
2. Был очень демотивирующий эффект на чтение учебника дальше положенного. Я понял, что если я учу что-то сам, то должен запоминать что мы проходили в школе, а что я читаю сам.
Самое интересное, что потом на контрольных, и гос экзаменах всем как раз уже было срать на ход решения и важен был правильный результат
Ну я думаю, что если во втором классе школьник найдет площадь прямоугольника интегрированием, то ему тоже не засчитают задание :)
раскрыть ветку (1)
Если он это повторил у доски самостоятельно, то я бы не просто засчитал, я бы его по имени-отчеству стал называть)))
Да. Ты должен показать, что понял учителя.
Умный - напиши рядом второй вариант или попробуй доказать учителю, что ты тоже прав, но вариант, которому тебя учили, ты должен привести тоже. Задача-то в школе не просто ответ получить, а показать, что ты понял процесс получения :)
раскрыть ветку (7)
Фигня какая-то, как по мне. Имхо, если проходите умножение, то сразу говорите, что оно коммутативно. А то пару лет вдалбливают, что порядок множителей имеет значение, потом резко говорят, что не имеет. А потом идешь на вышку и оказывается, что где-то имеет, а где-то нет. Доколе?!?!?!?! )))
раскрыть ветку (6)
Вы давно в последний раз вспоминали как вас учили буквы писать? Если давно - загуглите прописи. И ведь долго учили. Сравните со своим нынешним почерком. Правда дураки?
раскрыть ветку (5)
Я, видимо, еще до конца не проснулся, связи не вижу...
И кого я дураками назвал? Просто ребенок решил задачу? Решил. Ответ правильный? Правильный. Другим способом решил? Ну напиши просто рядом, что мы тут тему другую проходим, или спроси, с пониманием он это сделал или кто-то подсказал. А не черкай все нафиг, убивая в маленьком человеке немного иной взгляд на вещи. Вдалбливать делать все под копирку неправильно, нужно учить получать результат и критически мыслить.
раскрыть ветку (4)
И кого я дураками назвал?
По-моему, это я назвал :)
В школе главное не ответ, а решение. Умеешь решать другим способом? Молодец, но не забудь показать, что ты понял и то, что тебе рассказывали на уроке. Ответ без решения это очевидная двойка. Решение, в котором ошиблись с ответом может быть и четыре и пять с минусом, в зависимости от серьёзности ошибки.
В школе тебя учат думать и рассуждать, а "ответ" ты и на калькуляторе получишь :)
раскрыть ветку (3)
В школе тебя учат думать и рассуждать
Исходя из ваших слов в школе учат работать по алгоритму. Шаг влево, шаг вправо - расстрел.
Ладно, не буду спорить. Я не педагог и не психолог. Просто по своему опыту сужу. Когда пришел на мат. фак. учиться, то понял, что в школе что-то не то. М.б. меня только так учили, а другие школы клевые, хз. )
раскрыть ветку (2)
Можно подумать на матфаке "главное это ответ" прокатывало :) Вы мне сказки-то не рассказывайте, у меня за плечами матшкола и кафедра прикладной математики :)
раскрыть ветку (1)
Если в задаче вопрос "сколько", то главное ответ. Если "докажи", то нужно доказать. Если важен способ решения, то всегда писали каким методом решить. Если что-то свое придумаешь, так с преподавателем еще пообсуждаешь. Никогда никто не говорил "это неправильно, потому что не так, как я учил/учила".
тогда он не понимает какую задачу перед ним ставит учитель. от него требуют не число , его вообще можно не ставить , а правильно расставленные множители.
раскрыть ветку (1)
В задаче вопрос "Сколько". Ответ - число. Хотите правильный ответ - задайте правильный вопрос.
и да, у сына в классе учительница так и сказала, что в младших классах учат не просто перемножить, а понимать что и сколько раз взято и при проверке неправильная расстановка множителей считается грубой ошибкой, тогда как в средней и старшей школе, на это уже не обращают внимания, потому что дети уже понимают что к чему)
раскрыть ветку (2)
вот объясните пожалуйста, с какой целью в умножении нужно понимать "что и сколько раз взято"? для чего это понимание нужно? количество - величина безразмерная вообще-то.
раскрыть ветку (1)
при решении примеров, это не важно. При решении задач на 1е место ставится то, что нужно найти. Нужно найти кол-во ящиков- ставите ящики, если кг- значит кг. Для средних и старших классов это однофигственно, а в началке считают за ошибку.
Понимание математики приходит с понимаем того, что операции сложения и умножения имею свойство коммутативности (это как раз про а*в = в*а).
Но, как я вижу, тут и некоторые взрослые-то даже слова такого не знают. Придумывают какие-то "преместительные законы" и на серьезных щщах рассуждают про понимание математики.
раскрыть ветку (9)
UPD: Немного перегнул. Оказывается в учебниках действительно фигурирует термин "переместительный закон". Извините, если грубо выразился.
раскрыть ветку (6)
Ну только не говори что в школе тебе сразу во 2 классе про коммутативность и дистрибутивность рассказывали
раскрыть ветку (5)
Я как бы с садика подозревал об отрицательных числах. Я видел термометр, слышал о долгах и прочем. В школе мне упорно гоалрили "рано", а меня все мучал вопрос о отрицательных велечинах и я изучил их сам(в прямом смысле, сел и вывел, на умножение правда мозгов не хватило).
Тоже самое с умножением. Я еще таблицу изучая(правда нам уже преподавал список примеров) нашел закономерности и понял, что учить можно ровно половину.
В более старших классах я пытал преподов на предмет "а хули площадь круга именно такая", в ответ "рано". Ну еб вашу мать объясни ты про интеграл
раскрыть ветку (4)
Проблема сугубо в том, что программа общеобразовательная, и тут как раз надо учителю равняться на средний уровень, а вы как ученик с отрицательными числами вносили смуту.
раскрыть ветку (2)
По рассказам родителей я умел дикую штуку. Умножать на пальцах двузначные числа, причём быстро и точно. Учительницу это жутко бесило и она требовала отучить и родители отучили, о чем сильно жалеют. Сейчас ни они, ни я не помнят как я это делал и какой системой пользовался, но по историям я делал это осмыслено.
Вот так в нашей семье была утеряна технология пальцевого умножения.
P.S. к чести родителей они сперва говорили учителю "а вы сами можете как он? На бумажке в столбик и дурак сможет, а вы на пальцах устно"
раскрыть ветку (1)
Согласен, с вами, быть одаренным не всегда легко, учительницу бесило, что своими действиями вы подрывали ее авторитет.
Отрицательные числа интуитивно понятная вещь, я тоже с садика о них знал.
Но сомневаюсь что тебе именно слово "коммутативность" говорили
Первый адекватный комментарий по методике преподавания.
Сначала родители убеждают своих детей, что учителя - дебилы, а потом удивляются, что дети учителей ни во что не ставят и, соответственно, за всю школу ничему не научились.
раскрыть ветку (8)
раскрыть ветку (7)
Как раз тут учитель ничего не придумывал. Комментатор выше же ясно объяснил, что такое умножение: a * b = a + a + a + ... + a (b раз)
Свойство коммутативности умножения они ещё не прошли, не доказали, поэтому его применение неправильно в данном случае.
Я не раз сталкивалась со школьниками, которые не могут решить элементарные задачи просто потому, что не способны понять, что и в какой последовательности надо делать. У этого непонимания ноги растут как раз из вот таких "мелочей", как этот пример.
А родители (и другие взрослые), возмущающиеся тому, что учитель "всякий бред пишет" и "неправильно оценивает работы" способствуют тому, что школьники в дальнейшем не могут простроить себе нормально математическую систему.
ещё комментарии
"Я не раз сталкивалась со школьниками, которые не могут решить элементарные задачи просто потому, что не способны понять, что и в какой последовательности надо делать."
Потому что дебильные учителя учат по дебильным программам.
Которые "разрабатываются" каждый год ради написания очередных дебильных диссертаций.
И ради выпуска новых учебников, побольше и потяжелее. И, естественно, подороже.
Свойство коммутативности умножения они ещё не прошли, не доказали,
Коммутативность умножения — это аксиома. Она не доказывается.
раскрыть ветку (4)
Откуда у вас такие странные представления?
Доказывается коммутативность и сложения, и умножения
раскрыть ветку (2)
Вот, к примеру, из «Математического анализа» Зорича. В принципе, есть и другие способы построения множества действительных чисел, но я нигде не встречал, чтобы коммутативность была теоремой.
раскрыть ветку (1)
Тут другое определение умножения, видите же.
Если определять умножение через сложение, то нужно доказывать.
Тем, кто молча влепил мне 8 минусов: ну так приведите доказательство коммутативности. Или ставите минусы просто так, ничем не обосновывая?
ещё комментарии
люди не могут понять простого: взять 3 пенала 4 раза не то же самое.что взять 4 ручки по 3 раза
раскрыть ветку (1)
Проблема в том, что никто родителям не объясняет этот подход, а родители подсказвают и объясняют решение на основе своих знаний
раскрыть ветку (3)
Я думаю, что родители просто забывают со временем. Эта тема, как кто-то из учителей тут объяснял, не меняется давным давно, ещё с советских времён.
P.S. Я, к примеру, только глядя на пост вспомнил, что в школе писали знак умножения как току.
раскрыть ветку (2)
Не было такого в советские времена! Я в семидесятых начала учиться, никогда нам такое не исправляли. У меня старые тетради долгое время хранились, за перестановку чисел никаких санкций не было. Я отличница была до пятого класса, если бы за это снижали оценки, я бы не была отличницей, ибо про эти методы я узнаю только сейчас из таких вот постов.
раскрыть ветку (1)
Я не помню. Честно. Я в 78-м в первый класс пошёл - не помню. Но родители нынешних детей в большинстве своём учились позднее нас с вами.
Прошу прощения, прочитал про "переместительный закон умножения" и в выводе его написано: "От перестановки сомножителей произведение не меняется". И что в итоге то, какая разница ящики на апельсины умножать или апельсины на ящики? Это на столько смешно, что профессор по высшей математике от смеха падает.
раскрыть ветку (1)
Вобще-то от того, что на что умножать зависит количество битых апельсинов. Первое, с чем я столкнулся в высшей математике - это как раз отсутствие "переместительного закона умножения". Для каждого поля еще нужно доказать, работает этот закон или же нет (и в большинстве случаев он не работает, а работает только на скалярах)
Спасибо вам за этот комментарий! Всегда жопа горит от подобных публикаций! Сейчас только ленивый не пнет учителя.
Когда я объясняю ученикам деление в программировании целочисленное/вещественное, я провожу аналогии со школой, когда говорили что делить можно только нацело, потом оказалось что можно, а дальше начались извлечение корней из отрицательных чисел и деления на ноль. Тут так же, надо усвоить корректно материал, понять что и откуда, а потом двигаться дальше. А то в голове каша будет.
То есть надо взять 4 ручки три раза. Я правильно понимаю? А можно взять 3 раза 4 ручки. Не вижу разницы.
раскрыть ветку (4)
раскрыть ветку (3)
Закончил прикладную математику. И похоже не помогло. Подскажите. Господин ehanpalich написал правильный ответ?
раскрыть ветку (1)
Уважаемый hackoff подробно расписал в чем разница, я тоже как смог объяснил.
Не вижу смысла повторяться.
ещё комментарий
Это не заучивание, а критическое мышление. Благо моя учительница была не ебанутой и главной задачей у нее было научить детей решать, а не добываться по мелочам.
Спасибо, мил человек! Я сначала возмутился, мол какого хера!!! А про себя умножал 4х3 и не мог объяснить, что тут всё таки не так.
ещё комментарии
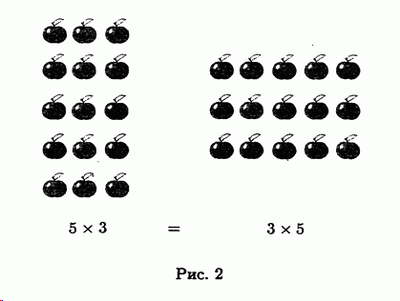
и переместительный закон становится понятен уже в графической форме когда видишь что это получаются столбцы и строчки. Все нормально. Думается это верная задача и скорей на следование правилам и логике чем вычислениям.
раскрыть ветку (1)
Он понятен уже на примере таблицы умножения, которая зеркальна относительно своей главной диоганали
раскрыть ветку (3)
О да, детям же не надо показывать, что иногда бывает недостаточно данных для решения задачи.
раскрыть ветку (2)
Школьный уголок
1.8K постов3.8K подписчика
Правила сообщества
Можно:
Писать всё, что можно отнести к школе.
...
Нельзя:
Нарушать правила Пикабу.